一、非线性假设

1.1 线性和非线性的区别

在机器学习中经常会遇到两个概念：线性、非线性，在线性代数中，线性有以下两个特征：

• 齐次性：$f(ax)=af(x);$
• 可叠加行：$f(x+y)=f(x)+f(y)$。

只要不满足其中一个条件则为非线性。

在机器学习中线性模型和非线性的区别：

1. 线性模型可以是用曲线拟合样本（即可以用单级感知机表达），但是分类的决策边界必须是直线的，例如logistics模型。
2. 区分是否为线性模型，主要是看一个乘法式子中自变量$x$前的系数$w$，如果$w$只影响一个$x$，那么此模型为线性模型。或者判断决策边界是否是线性的。

例如：

$y = \frac{1}{1+e^{w_0+w_1x_1+w_2x_2}}$ 虽然图像是个曲线，但是 对于 $x_1$ 只受 $w_1$ 影响，对于其他变量也是，所以是线性的。

$y = \frac{1}{1+w_3e^{w_0+w_1x_1+w_2x_2}}$ ，$x_1$ 同时收到 $w_3,w_1$ 影响，是非线性的。

1.2 回归算法的缺陷

很多情况下需要处理的问题都是非线性的，虽然Logstic回归和线性回归可以通过添加高次多项式的方式来拟合非线性的样本。但是，当属性值过多时 （比如在房价预测问题中，有诸如房间面积、卧室面积、房屋年龄等大量属性），需要添加的高次项会很多，这样会带来两个问题：1.计算耗时长。2. 容易操作过拟合。

当然可以通过减少一些高次项来解决这个问题，但是，这样就会造成欠拟合的问题。此外，即使是线性的样本，如果特征过多时，无论是Logistic回归还是线性回归都是不合适的。比如在计算机视觉领域，如果要识别某个图形，那么此图形的每个像素点的灰度都会作为一个特征，图片较大时特征就会很多。因此，回归算法并不能解决所有问题。

二、神经网络模型

2.1 逻辑单元（神经元）

在人脑中有数以亿计的神经元，每个神经元最主要的就是树突和轴突，树突接收来自外界的电信号，然后判断是否激活，如果激活则通过轴突发出电信号，电信号就会传向下一个与之连接的神经元，重复进行接收判断并发送的过程，当然一个神经元的树突可能连接多个神经元，其轴突也可能连接多个神经元，是多对多的关系。（个人非严谨的理解）而这里的电信号的发送与不发送就可以看成向后面传输0或1的数据。

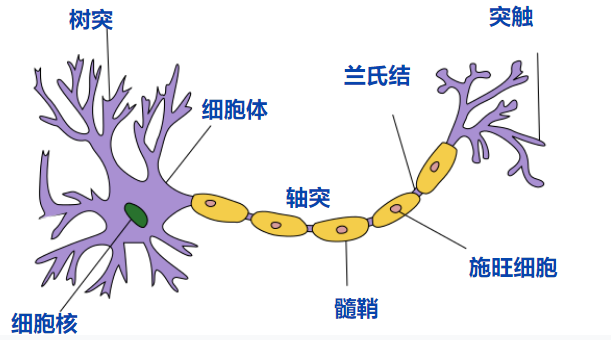
将生物的神经元抽象一下，就形成下面的这样一个模型，其中橙色的圈圈代表一个神经元，并且有三个神经元 $x_1 \ x_2 \ x_3$ 与之连接，橙色神经元接受三个神经元的输入进行计算后向右边输出一个值，注意，在计算机里的神经元输出可以是个数字,不一定只能是0或1，这个数字称为激活值。

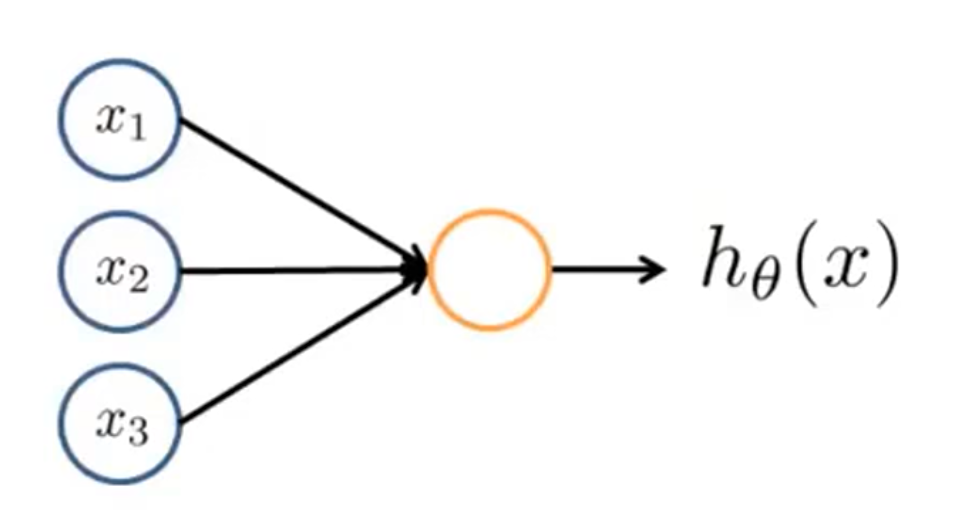
具体计算方法是，会预先给三条从 $x_1 \ x_2 \ x_3$ 连向橙色神经元的边赋上权值 称为 $\theta_1 \ \theta_2 \ \theta_3$ ，这里的 $\theta$ 称为模型的权重，也可以称之为参数，然后计算 $z = x_1\theta_1 + x_2\theta_2 + x_3\theta_3$ 。通常，我们不会直接输出 $z$ ，而是经过一个激活函数，使得模型具有非线性的表达能力（神经网络激活函数的作用和原理）同时使得输出的数值可以压缩在 $[0,1]$ 之间，这里我们使用和sigmoid函数作为激活函数，即$g(z) = \frac{1}{1+e^{-z}}$，这样的神经元又称其为带Logistic激活函数的人工神经元。

需要注意的是，在计算神经元的激活值时还会加入一个 $x_0 = 1$用于调整激活值，称其为偏置单元，则$z = x_0\theta_0 + x_1\theta_1 + x_2\theta_2 + x_3\theta_3$ ，在画图中一般省略，但是在计算过程中不能省略，不然可能会导致最后模型无法收敛。在后面的反向传播中，模型会自主地调节所有边权即 $\theta$ 的值，加入一个偏置单元的作用可以理解成用于调整神经元的激活门槛，比如我们不想让这一层的神经元很容易地激活（即输出较高的值），那么就可以利用偏置单元的权重 $\theta_0$ 将其设成一个很大的负数，使得权值变得很小。当然也可以从几何的角度去理解，其实就是使得超平面可以自主地平移，划分出合适的决策边界：神经网络中的偏置项b到底是什么？。

参考视频：3Blue1Brown【官方双语】深度学习之神经网络的结构 Part 1

2.2 神经网络

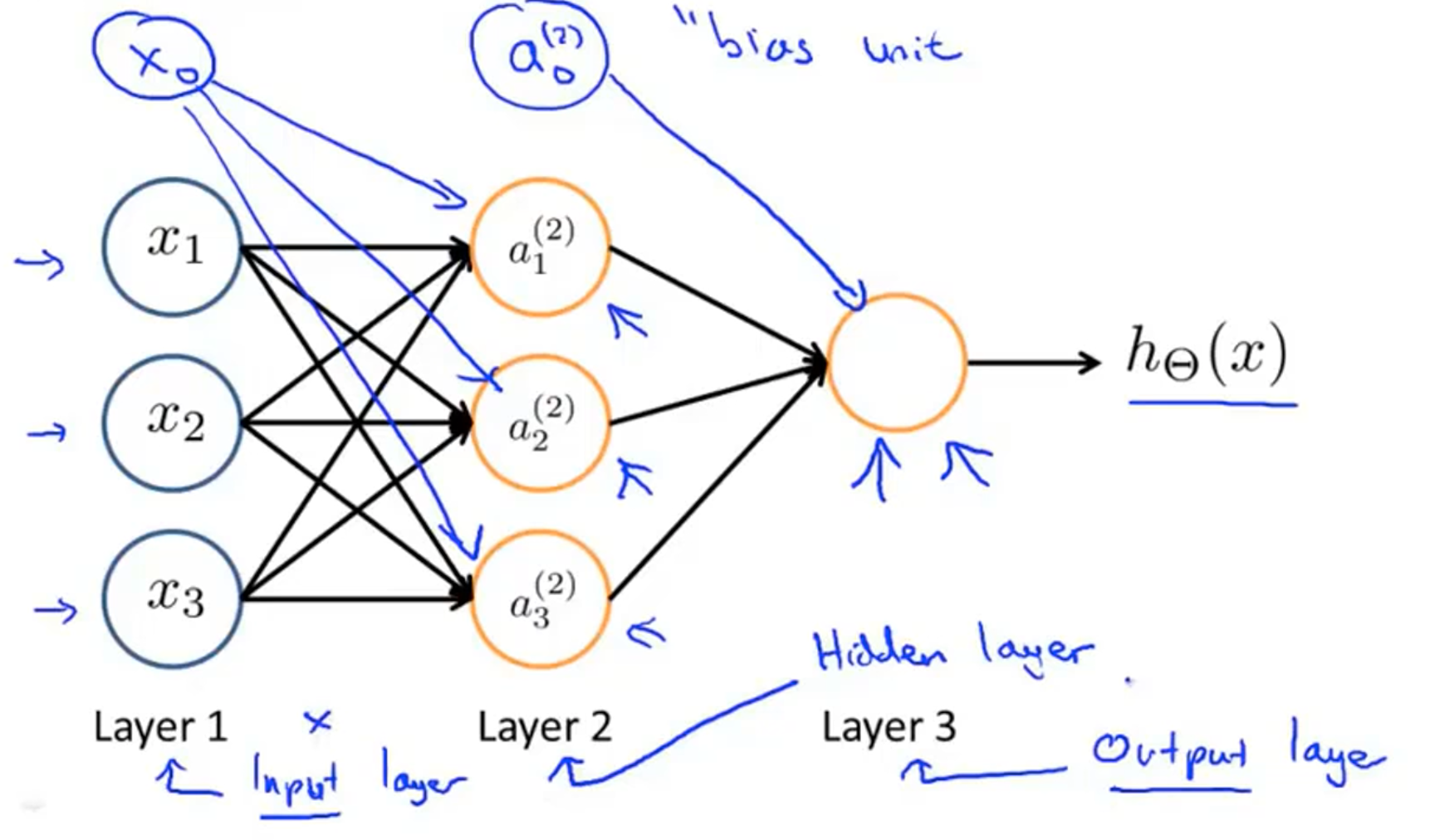
如上图所示的就是一个神经网络的模型，就是多个神经元组合而来的，第一层称为输入层， 第二层称为隐藏层， 第三层称为输出层。神经网络中的隐藏层可能有很多层（只要不直接与外界进行输入输出的就成为隐藏层），且隐藏层中的值是不显示的。其中，$x_0$ 和 $a_0^{2}$ 表示偏置单元（有时省略不画出来），值都为1。

一些符号说明：

$a_i^{(j)}$ 表示第j层的第i个神经元的激活项，激活项指的是该神经元计算得到的值。

$\Theta^{(j)}$ 表示控制第 j 层向第 j+1 层转移的模型参数（权重）构成的参数矩阵。

由此，我们可以给出神经网络的激活函数：

$a_1^{(2)} = g(\Theta^{(1)}_{10}x_0 + \Theta^{(1)}_{11}x_1+ \Theta^{(1)}_{12}x_2+ \Theta^{(1)}_{13}x_3)$

$a_2^{(2)} = g(\Theta^{(1)}_{20}x_0 + \Theta^{(1)}_{21}x_1+ \Theta^{(1)}_{22}x_2+ \Theta^{(1)}_{23}x_3)$

$h_{\Theta}(x) = a_1^{(3)} = g(\Theta^{(2)}_{10}a_0^{(2)} +\Theta^{(2)}_{11}a_1^{(2)}+\Theta^{(2)}_{12}a_2^{(2)}+\Theta^{(2)}_{13}a_3^{(2)})$

规律： 如果第 $j$ 层有 $s_j$ 个神经元， $j+1$ 层有 $s_{j+1}$ 个神经元，则 $\Theta^{(j)}$ 是一个 $s_{j+1} * (s_j+1)$ 维的矩阵。注意这里 $s_j$ 要+1是因为还有一个偏置单元，这个单元一般是默认不画出的，计算个数时也不包括。

2.3 神经网络的向前传播

我们用 $z^{j}_i$ 表示第 $j$ 层第 $i$ 个神经元的加权计算值，对于上图的神经网络模型，可以得到：

$z^{(2)}_1 = \Theta^{(1)}_{10}x_0 + \Theta^{(1)}_{11}x_1+ \Theta^{(1)}_{12}x_2+ \Theta^{(1)}_{13}x_3$

$z^{(2)}_2 = \Theta^{(1)}_{20}x_0 + \Theta^{(1)}_{21}x_1+ \Theta^{(1)}_{22}x_2+ \Theta^{(1)}_{23}x_3$

$z^{(2)}_3 = \Theta^{(1)}_{30}x_0 + \Theta^{(1)}_{31}x_1+ \Theta^{(1)}_{32}x_2+ \Theta^{(1)}_{33}x_3$

对于$z^{(2)} = \left[\begin{matrix}z_1^{(2)}\\z_2^{(2)}\\z_3^{(3)}\end{matrix}\right]$,可以用矩阵乘法来计算，即$z^{(2)} = \Theta^{(1)}x$，其中$x = \left[\begin{matrix}x_0\\x_1 \\ x_2\\x_3 \end{matrix}\right]$,那么就有$a^{(2)} = g(z^{(2)})$，这里的$a^{(2)}$ 和 $z^{(2)}$ 都是3维向量，将函数 $g()$ 逐一作用于 $z^{(2)}$ 的每一个元素得到 $a^{(2)}$ 。由于 $x$ 实际上就是上图中第一层输入层的神经元，为了统一，我们可以把 $x$ 用 $a^{(1)}$ 代替，于是得到：$z^{(2)} = \Theta^{(1)}a^{(1)}$，$a^{(2)} = g(z^{(2)}) = g(\Theta^{(1)}a^{(1)})$。由于还有一个偏置单元，所以在 $a^{(2)}$ 中加入 $a^{(2)}_0 = 1$ ,使得 $a^{(2)}$ 变成一个4维的向量。接着就可以计算$z^{(3)} = \Theta^{(2)}a^{(2)}$ , 则最终的输出$h_{\theta}(x) = a^{(3)} = g(z^{(3)}) = g(\Theta^{(2)}a^{(2)})$。这种计算方法也称为向前传播，因为最终的值是通过输入层经过隐藏层一步一步向前传播计算得来的。

神经网络的本质：重新观察上述的神经网络模型，如果遮掉第一层，将第二层作为输入层，可以发现，这本质就是一个逻辑回归模型。这时我们就可以发现，神经网络的本质就是逻辑回归模型的套娃，每一层都会做若干次的逻辑回归，并将输出作为下一层的输入，然后下一层再利用上一次逻辑回归的结果进行逻辑回归得到结果再传给下一层，直到符合条件输出。

三、神经网络举例

3.1 问题引入

假如我们有下图右边的一个样本需要分类，很明显这是一个非线性的分类问题。我们研究这个问题的简化版本，假设 $x_1$ $x_2$ 为二进制数，则图像变成下图左，即求XOR异或，或者说是求 NOT XOR（异或取反，对于二元分类问题是等价的）。

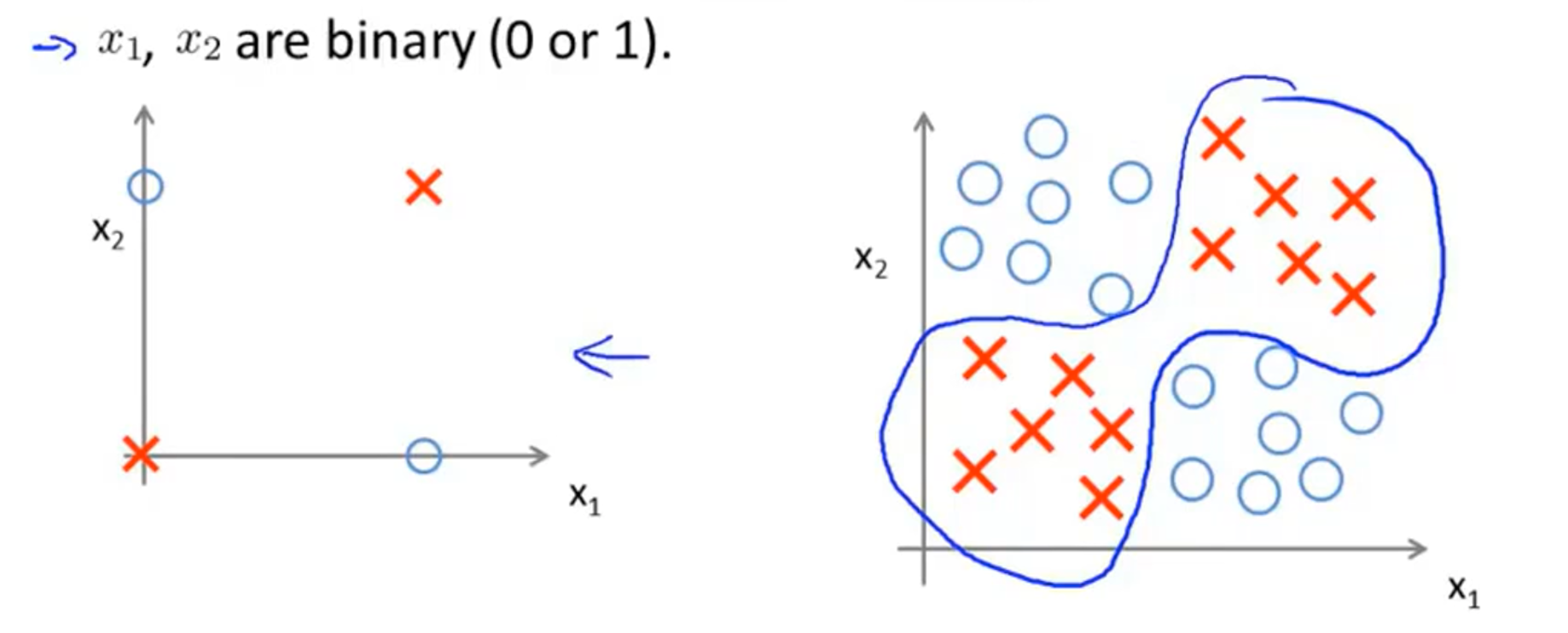
3.2 AND实现

在实现NOT XOR之前，我们可以先来看一个简单的运算——AND。我们可以用一个简单的神经网络来实现AND运算，如下图左，它不包含隐藏层，可以发现这个模型和回归算法十分相似。给出模型的参数，分别为-30，20，20，列出真值表，根据Logistic函数图像得到 $h_{\Theta}(x)$​ 的计算结果，如下图右，符合AND运算。

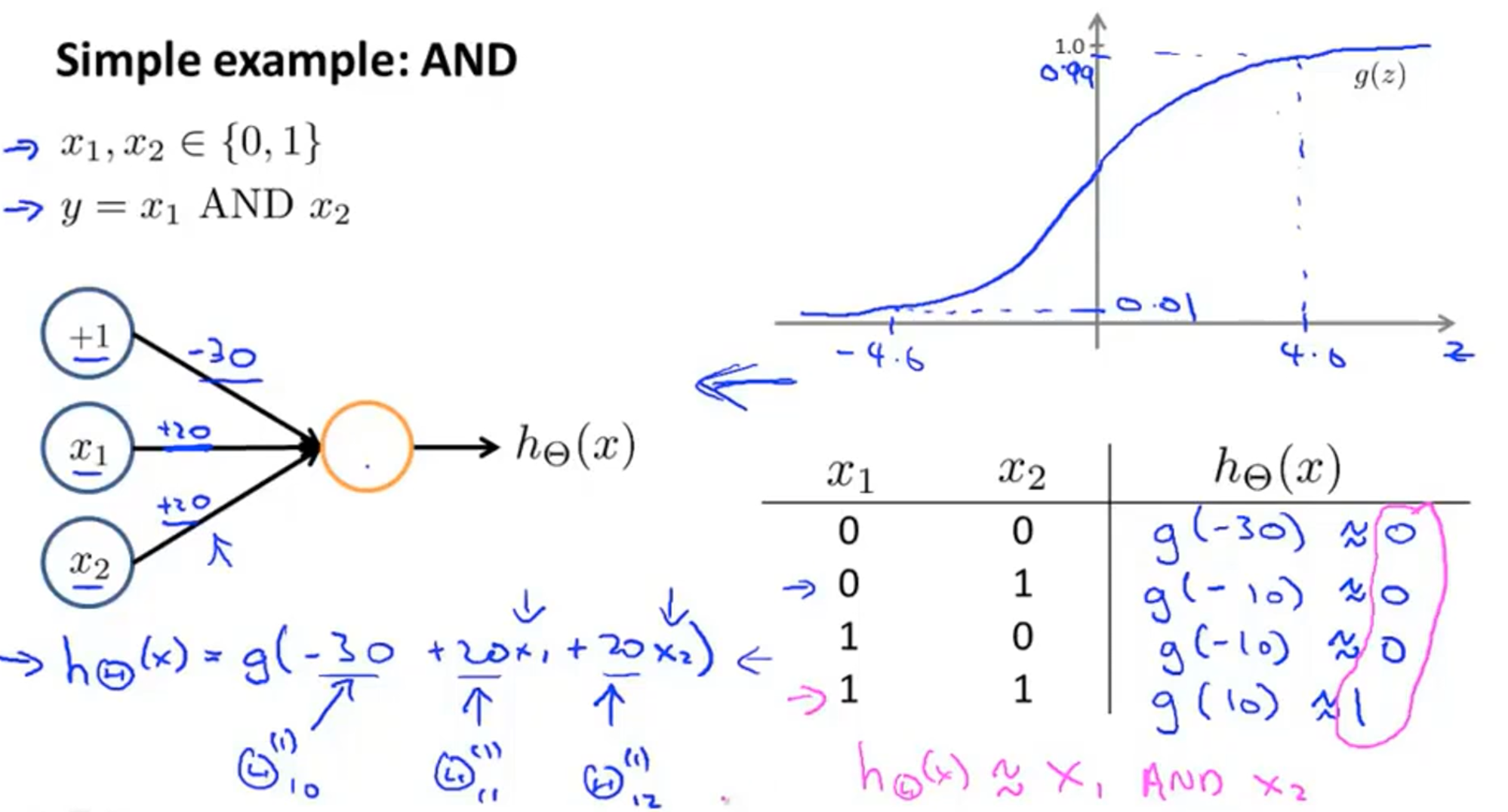
3.3 NOT XOR实现

上面实现了AND运算的神经网络，下面分别给出其他几个类似的运行对应的神经网络的模型：

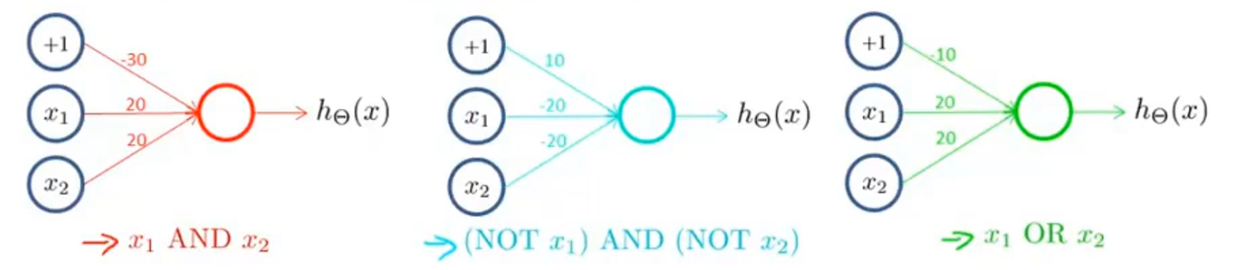
由上面的简单模型，我们就可以得到 NOT XOR 的神经网络了：

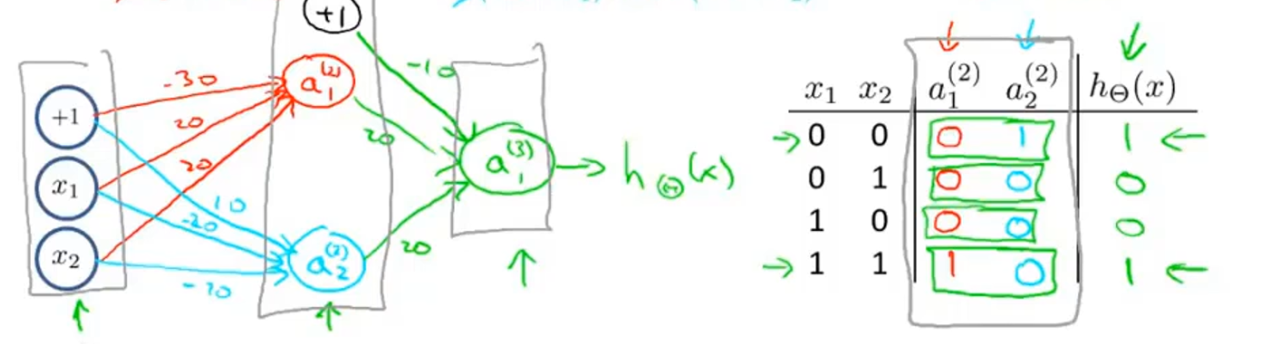
可以发现，其实 NOT XOR就是上面几个简单运算的组合，由此我们可以发现，其实神经网络的隐藏层其实就是分阶段实现不同复杂度的一个函数功能，一层一层增加复杂度最终得到解。

题外话：AND 和 OR 的实现只用到了一个神经元结构进行运算，这样的一个单元也叫做感知机模型，感知机模型可以用于解决线性可分的问题，但是不能解决线性不可分的问题（如XOR），这也使得神经网络的研究进入一段低谷，直到后来有人发明出BP（反向传播算法），才使得神经网络可以用于解决线性不可分问题，其中使得模型可以解决线性不可分的关键就在于激活函数。

四、多元分类

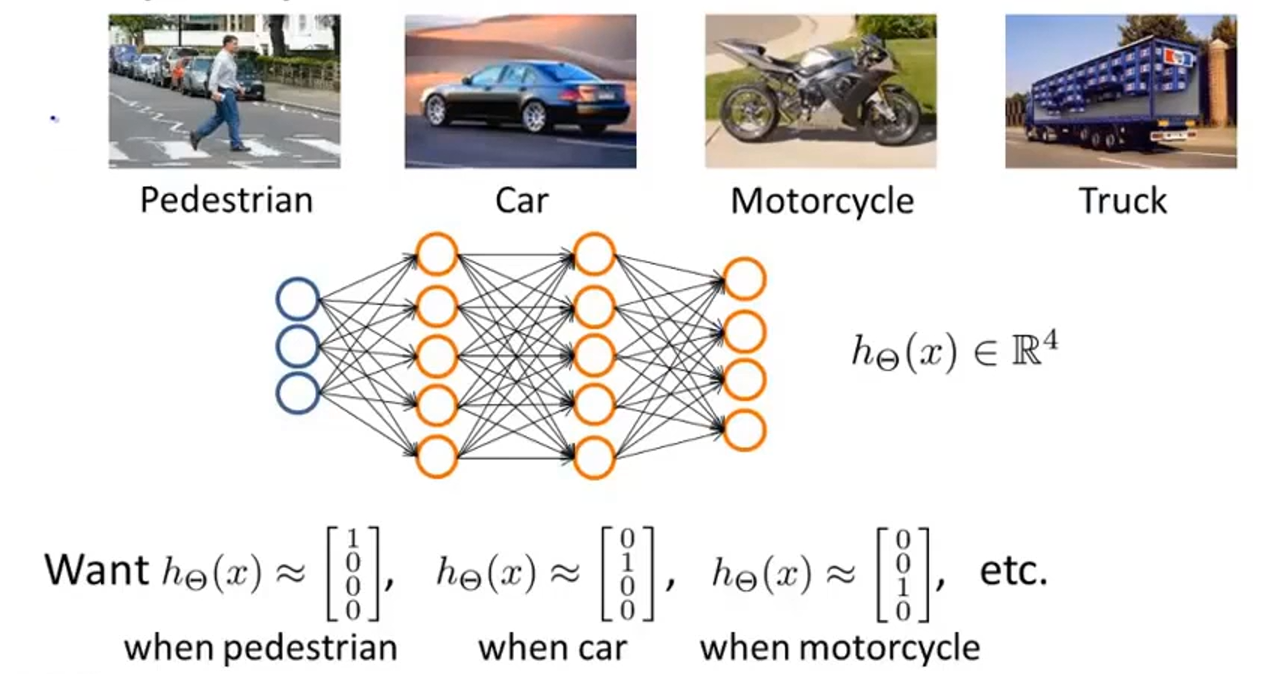
比如计算机视觉中的图片识别，将图片分为行人、汽车、摩托车、卡车四类，就是一个多元分类的问题，类似于线性回归中解决多元分类问题的一对多思想一样，神经网络也类似，建立如上图的神经网络，最终的输出为一个四维向量，如果为1000，则表示是行人，0100表示是汽车，以此类推。