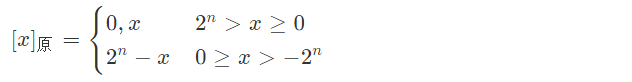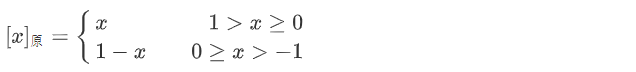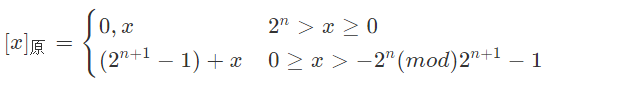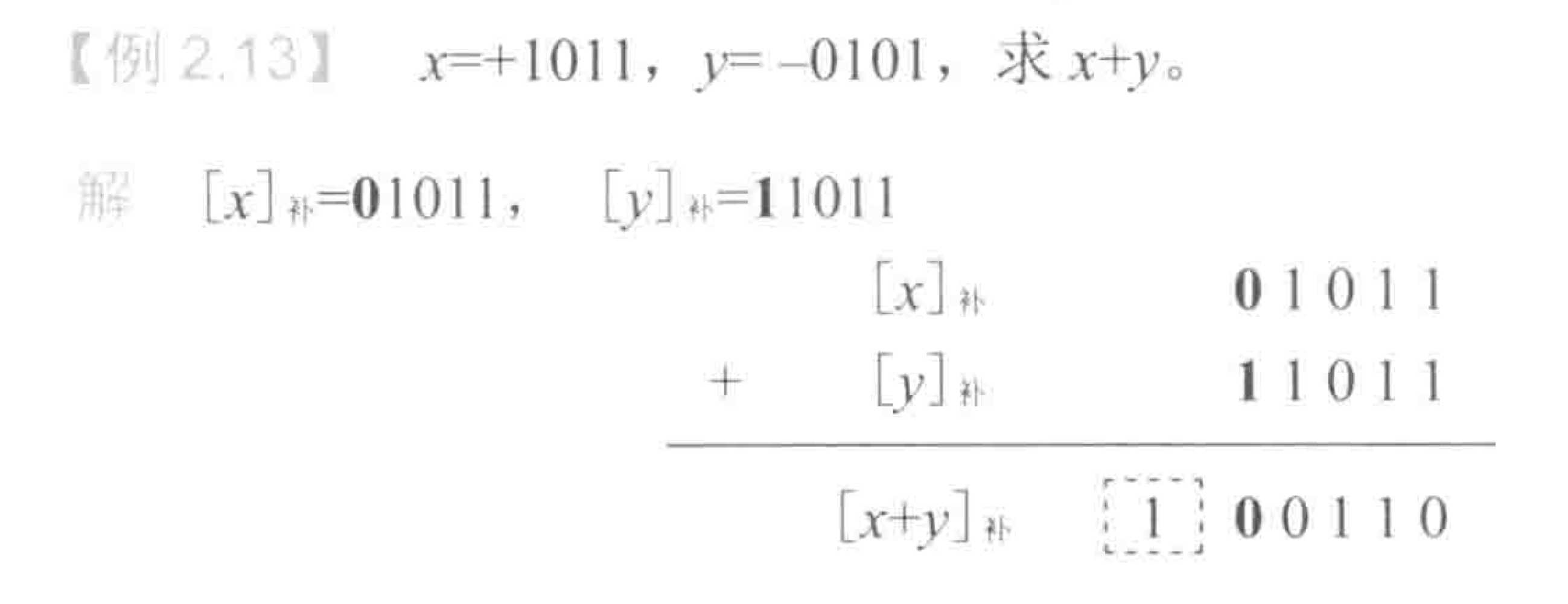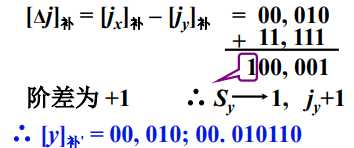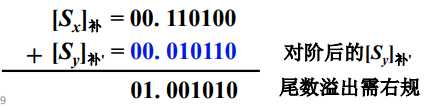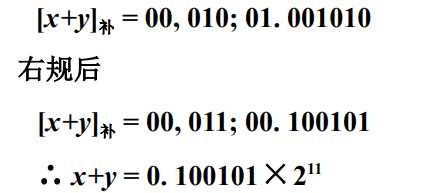2.1 数据与文字的表示方式
2.1.1 数据格式
1.定点数表示法
将数据分为纯整数和纯小数两类,用n+1位表示一个定点数,$x_n$为符号位,放在最左边,0表示正号,1表示负号。故一个数 $x$ 可以表示为 $x = x_nx_{n-1}…x_1x_0$
$x$为纯小数:$0\leq |x|\leq 1-2^{-n}$
$x$为纯整数:$0\leq |x| \leq 2^n-1$
计算机中多采用定点纯整数表示,将定点数表示的运算简称整数运算。

2.浮点数表示法
小数点随着阶码的不同而浮动,数的范围和精度分别表示。
格式:$N = R^e.M$
$M$称为浮点数的尾数,$e$ 称为指数,是一个整数,R是基数,一般隐式表示(通常2或10)。在机器中,尾数用定点小数形式表示,指数用定点整数形式表示,称为阶码。

3. 浮点数表示范围

4. 浮点数的规格化
规格化形式:
- 基数 r = 2 ,尾数最高位为 1
- 基数 r = 4 ,尾数最高 2 位不全为 0
- 基数 r = 8 ,尾数最高 3 位不全为 0
基数不同,浮点数的规格化形式不同。
规格化方式:
- r = 2 左规 尾数左移 1 位,阶码减 1
右规 尾数右移 1 位,阶码加 1 - r = 4 左规 尾数左移 2 位,阶码减 1
右规 尾数右移 2 位,阶码加 1 - r = 8 左规 尾数左移 3 位,阶码减 1
右规 尾数右移 3 位,阶码加 1
基数 r 越大,可表示的浮点数的范围越大,基数 r 越大,浮点数的精度降低。
举例:
1.设 m = 4,n = 10,r = 2,求尾数规格化后的浮点数表示范围。
最大正数 = $2^{+1111} * 0.1111111111 = 2^{15} * (1-2^{-10})$
最小正数 = $2^{-1111} * 0.1000000000 = 2^{-15} * (2^{-1}) = 2^{-16}$ (尾数第一位规格化后必须为1)
最大负数 = $2^{-1111} * -0.1000000000 = -2^{-15} * 2^{-1} = -2^{-16}$
最小负数 – $2^{+1111} * -0.1111111111 = -2^{15} * (1-2^{-10})$
例 6.13 将 x = + 19/128 写成二进制定点数、浮点数及在定点机和浮点机中的机器数形式。其中数值部分均取 10 位,数符取 1 位,浮点数阶码取 5 位(含1位阶符),尾数规格化。
x的二进制表示: 设 x = + 19/128
二进制形式: $x = 0.0010011$
定点表示: $x = 0.0010011000$
浮点规格化: $x = 0.1001100000 * 2^{-10}$
定点机中: $[ x ]_ 原 = [ x ]_ 补 = [ x ]_ 反 = 0.0010011000$
浮点机中:
$[ x ]_ 原 = 1,0010;0.1001100000$
$[ x ]_ 补 = 1,1110;0.1001100000$
$[ x ]_ 反 = 1,1101;0.1001100000$
5. 十进制数表示
- 字符串形式
即一个字节存放一个十进制的数位或符号位,还需要存放该数在主存中的起始地址和该数的位数。 - 压缩的十进制数串形式
即一个字节存放两个十进制的数位或符号位即BCD码(压缩),即一个字节存放两个十进制的数位或符号位即BCD码(压缩)。
2.1.2数的机器码表示
1. 原码表示法
(1) 数学定义
- 整数:
整数的第一位为符号位,用 “,”隔开,0表示正数,1表示负数,x为真值,n为整数的位数。
- 小数:
(2) 举例
$[ x ]_原 = 1.001 $ $x = -0.001$
$ [ x ]_原 = 0.101 $ $x = +0.101$
$[ x ]_原 = 1,110 $ $x = -110$
$ [ x ]_原 = 0,011 $ $x = +011$
结论:有逗号表示整数,有小数点表示小数,符号前的数表示符号,0表示正数,1表示负数。
(3) 特点
简单、直观,但是在加法运算时由于符号位的存在,不能简单地按位相加,“+0”和“-0”的原码不同。
2.补码表示法
(1) 补的概念
- 以时钟为例,在时钟上进行运算相当于是模12下的运算。如果要-3,有两种途径:把指针向后拨3位(-3)或者向前拨9位(+9),故可以用这种方式将减法转换成加法,我们称+9是-3在模12下的补数。
- 结论:
- 一个负数加上“模”就是它的补数(如-3+12=9,表示-3在模为12下的补数是9)。
- 一个正数和一个负数互为补数时,他们绝对值之和即为模数(相当于结论1的逆运算)。
- 正数的补数就是其本身。
- “+0”和“-0”的补码相同
(2) 补码的定义
(勘误:下方公式的下标应该为“补”)
- 整数:
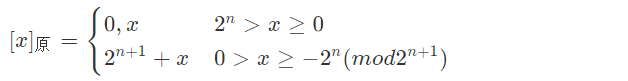
- 小数:
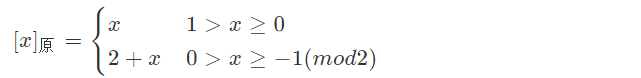

(4) 快速求补码
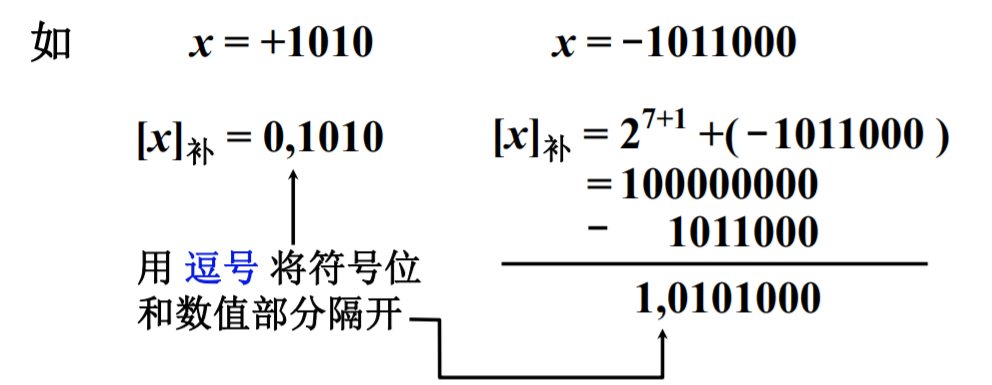
当真值为负数时,补码可以用原码忽略符号位每位取反后末位+1得到,再将符号位填1。
如:x = -1010,取反得0101,+1得0110,加上符号位得补码:1,0110。
原因如下:
根据补码的最初定义,$[ x ]_ 补 = 2^{n+1} + x$,假设x是个4位负数,用 $-x_1x_2x_3x_4$ 表示,那么公式可以写成 $[x]_ 补 = 2^5 – x_1x_2x_3x_4 = 100000 – x_1x_2x_3x_4 = 11111 + 00001 – x_1x_2x_3x_4$ ,而对于 $11111-x_1x_2x_3x_4$ 就可以看成 $1 \bar{x_1}\bar{x_2}\bar{x_3}\bar{x_4}$ ,然后再加上一个 $00001$ 。即除符号位外,每位取反,末位+1。
所以,已知x的补码,也可以很容易地求得-x的补码,即整体取反+1。树状数组的关键函数lowbit用于求一个数从末尾开始的第一个1所在位置的十进制数,其实现方式就是x & -x,用的就是这里的原理。
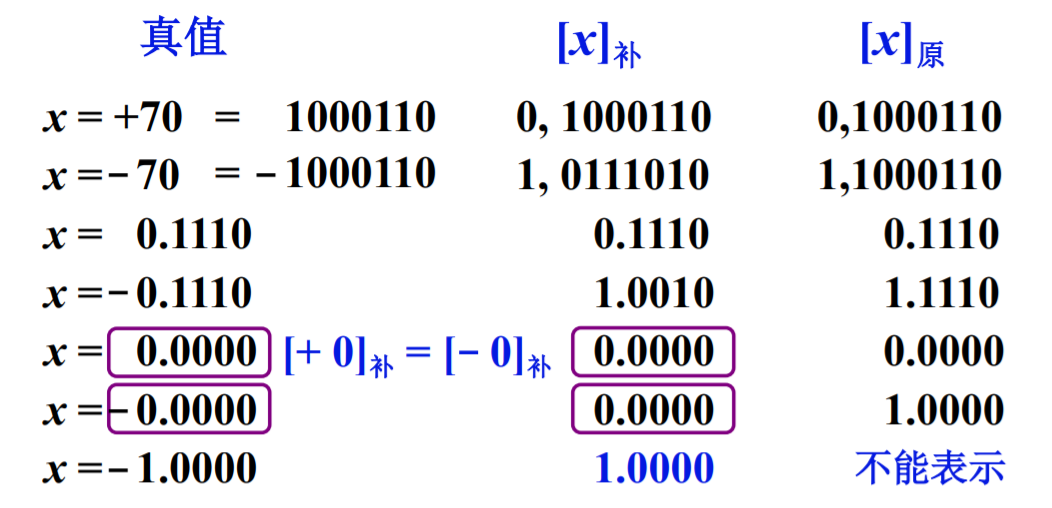
3.反码表示法
(1) 定义
(勘误:下方公式的下标应该为“反”)
- 整数:
-
小数:
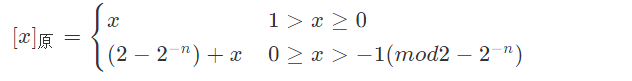
即 当真值为负数时,反码可以用原码除符号位外每位取反得到,正数反码不变,“+0”和“-0”的反码不同。
4. 三种表示法小结
- 最高位为符号位,书写上用“,”(整数) 或“.”(小数)将数值部分和符号位隔开。
- 对于正数,原码 = 补码 = 反码。
- 对于负数 ,原码符号位为 1,数值位不变,原码除符号位外取反后得反码,反码末位+1得补码,补码符号位取反得移码,补码连同符号位取反后+1得相反数的补码。
一字节空间可以表示的范围:

疑问:加蓝处为何为-128?
答:二进制代码10000000表示负数,忽略符号位取反后+1得到其补码也为1000000,如果按照原码的定义,10000000表示-0,但是补码没有“+0”和“-0”之分,补码的0全用00000000表示,多出的“-0”用于表示-128,所以补码比其他都多一个最小数。
5.移码表示法
(1) 定义
由于符号位存在,补码很难直接判断真值大小。
$[ x ]_移 = 2^n + x (2^n > x \geq -2^n)$x为真值,n为整数的位数。
$x = 10100,[ x ]_移 = 2^5+10100 = 1,10100$
$x = -10100,[ x ]_移 = 2^5-10100 = 0,01100$
移码与补码只差一个符号位,符号位取反两者就能相互转换。
证明:
正数:$[ x ]_ 补 = 0,x$ $[ x ]_ 移 = 2^n + x $,相当于在第n为 +1,即在符号位取反。
负数:$[ x ]_ 补 = 2^{n+1}+x = (2^n+x) + 2^n = [ x ]_ 移 + 2^n$,也相当于符号位取反。
(2) 特点
$[ +0 ]_ 移 = [ -0 ]_ 移$
最小真值的移码为全 0,用移码表示浮点数的阶码,能方便地判断浮点数的阶码大小。
6. IEEE754标准
IEEE二进位浮点数算术标准(IEEE Standard for Floating-Point Arithmetic)的标准编号,它规定了浮点数在计算机当中的存储方式以及算术标准等。
浮点格式可分为符号位s,指数位e以及尾数位f三部分。
规定了单精度(32)和双精度(64)两种基本格式(还有其他特殊格式不做介绍),规定尾数用原码,阶码用移码表示,但是不完全等同与移码,真值和阶码的转换为:单精度 $E=e+127$ ,双精度 $E=e+1023$ , $E$ 为阶码, $e$ 为指数真值。尾数域最高位总是1,隐藏在小数点左边不显示。
在IEEE-754 标准下,浮点数一共分为:
- NaN:即Not a Number。非数的指数位全部为1 同时尾数位不全为0。在此前提下,根据尾数位首位是否为1,NaN 还可以分为SNaN 和QNaN 两类。前者参与运算时将会发生异常。
- 无穷数:指数位全部为1 同时尾数位全为0,根据符号决定正负。
- 规格化数:指数位不全为1 同时尾不全为0。此时浮点数的隐含位有效,其值为1。
- 非规格化数:指数位全为0 且尾数位不全为0。此时隐含位有效,值为0。另外需要注意,以单精度时为例,真实指数E 并非0-127=-127,而是-126,这样一来就与规格化下最小真实指数E=1-127=-126 达成统一,形成过度。
- 0 :指数位与尾数位都全为0,根据符号位决定正负。
2.1.3字符与字符串的表示方法
符号数据:字符信息用数据表示,如ASCII等;
ASCII:用一个字节来表示,低7位用来编码(128),最高位为校验位,
字符串的存放方法:可以从低位到高位存放也可以从高位到低位存放。
2.1.4 汉字的表示方法
1. 汉字的输入编码
数字编码 拼音码 字形编码
2.汉字内码
汉字信息的存储,交换和检索的机内代码,两个字节组成,每个字节高位都为1(区别于英文字符)。
汉字字模码
用点阵表示汉字字形,形成汉字库。
输入编码用于输入,汉字内码用于计算机内部处理,字模码用于汉字输出。
2.1.5 校验码(奇偶校验)
设$x = x_0x_1…x_{n-1}$是一个n位字,奇校验位C定义为:$\bar{c} = x_0 \bigoplus x_1 \bigoplus…\bigoplus x_{n-1}$,即只有x中有奇数个1时才会使得c = 0。
奇偶校验码只能检测奇数个错误,无法检测偶数个错误,更不能提供错误的位置。
2.2定点加减法运算
2.2.1 补码加法
公式:$[ x ]_ 补 + [ y ]_ 补 = [x+y]_ 补$
补码加法特点: 符号位一起参与运算,在模 $2^{n+1}$ 下运算,即溢出舍去。
2.2.2 补码减法
公式: $[ x-y ]_ 补 = [ x ]_ 补 – [ y ]_ 补 = [ x ]_ 补 + [ -y ]_ 补$
已知y的补求-y的补方法: 连同符号位取反后末尾+1。
2.2.3 溢出概念与检测方法
1.定义
定点整数机器中,数的表示范围$|x| < 2^n-1$ ,在运算过程中出现大于字长绝对值的现象称为溢出。两个正数相加,结果大于机器字长所能表示的最大正数(变成负数),称为正溢。两个负数相加,结果小于所能表示的最小负数,称为负溢。
2.双符号位法判断溢出
$[ x ]_ 补 = 2^{n+2}+x (mod2^{n+2})$
$[ x ]_ 补 + [ y ]_ 补 = [x+y]_ 补 (mod 2^{n+2})$
规则: 两个符号位一起参与模$2^{n+2}$下的运算,符号位为11表示负数,00表示正数,01和10表示溢出,最高符号位表示正确的符号,01为正溢,10为负溢。
3.单符号判断溢出
当符号位产生进位而最高有效位没进位时发生负溢,当符号位无进位而最高有效位进位时发生正溢。
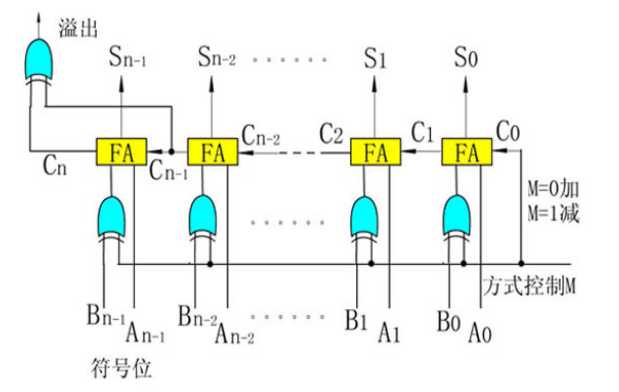
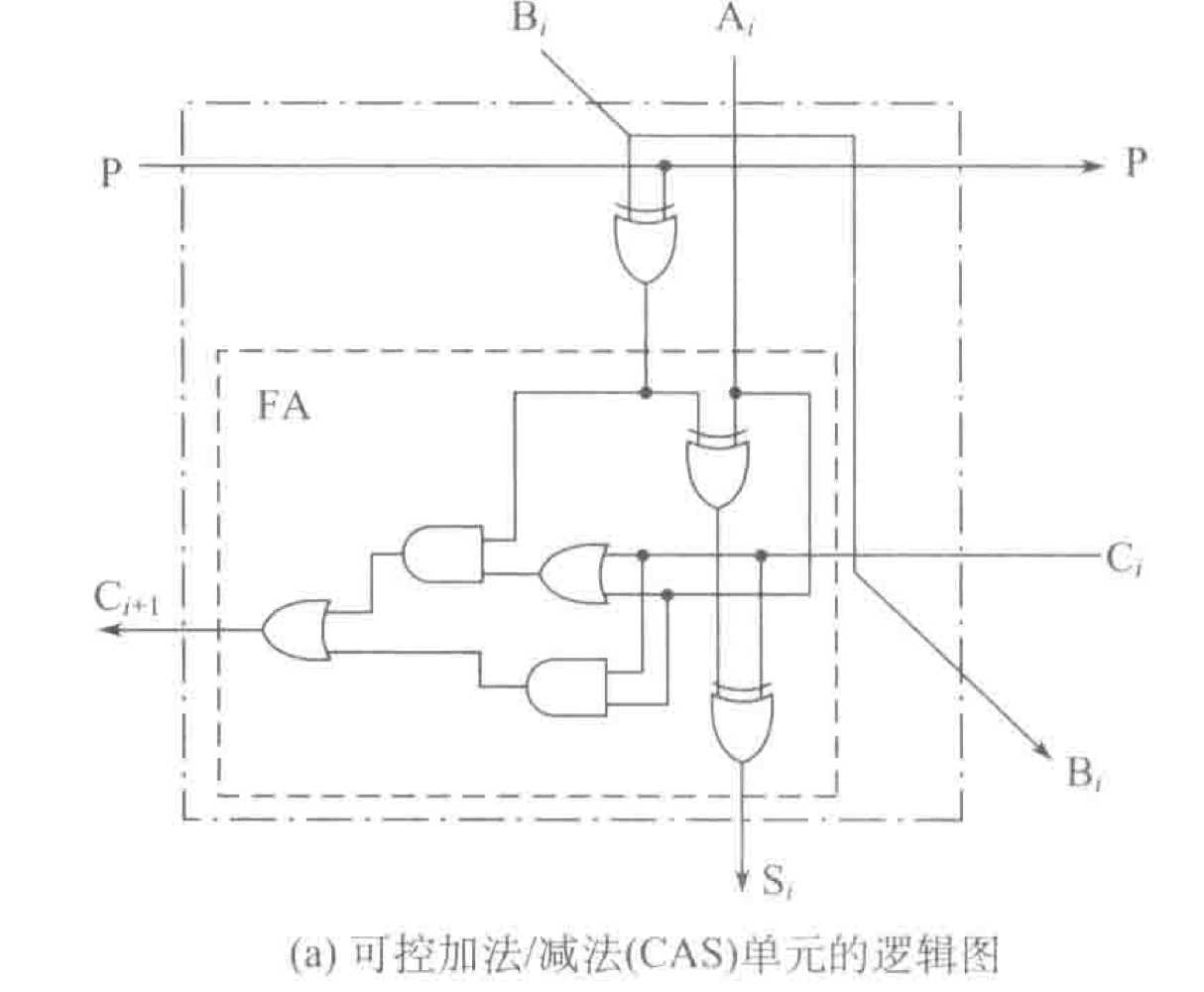
2.2.4 基本的二进制加法/减法器
由n个1位的全加器(FA)串联组成,全加器包含三个输入(两个加数,一个前驱进位数)和两个输出(结果和进位)。M为方式控制输入线,M=0时做加法,M=1时做减法。
减法实现: 通过 $[ A-B ]_ 补 =[ A ]_ 补 + [ -B ]_ 补$ 实现,-B的补码就是B连同符号位取反后+1,电路中通过一个异或门将B与1异或实现每位取反,$C_0$输入1实现末尾+1。
2.3 定点乘法运算
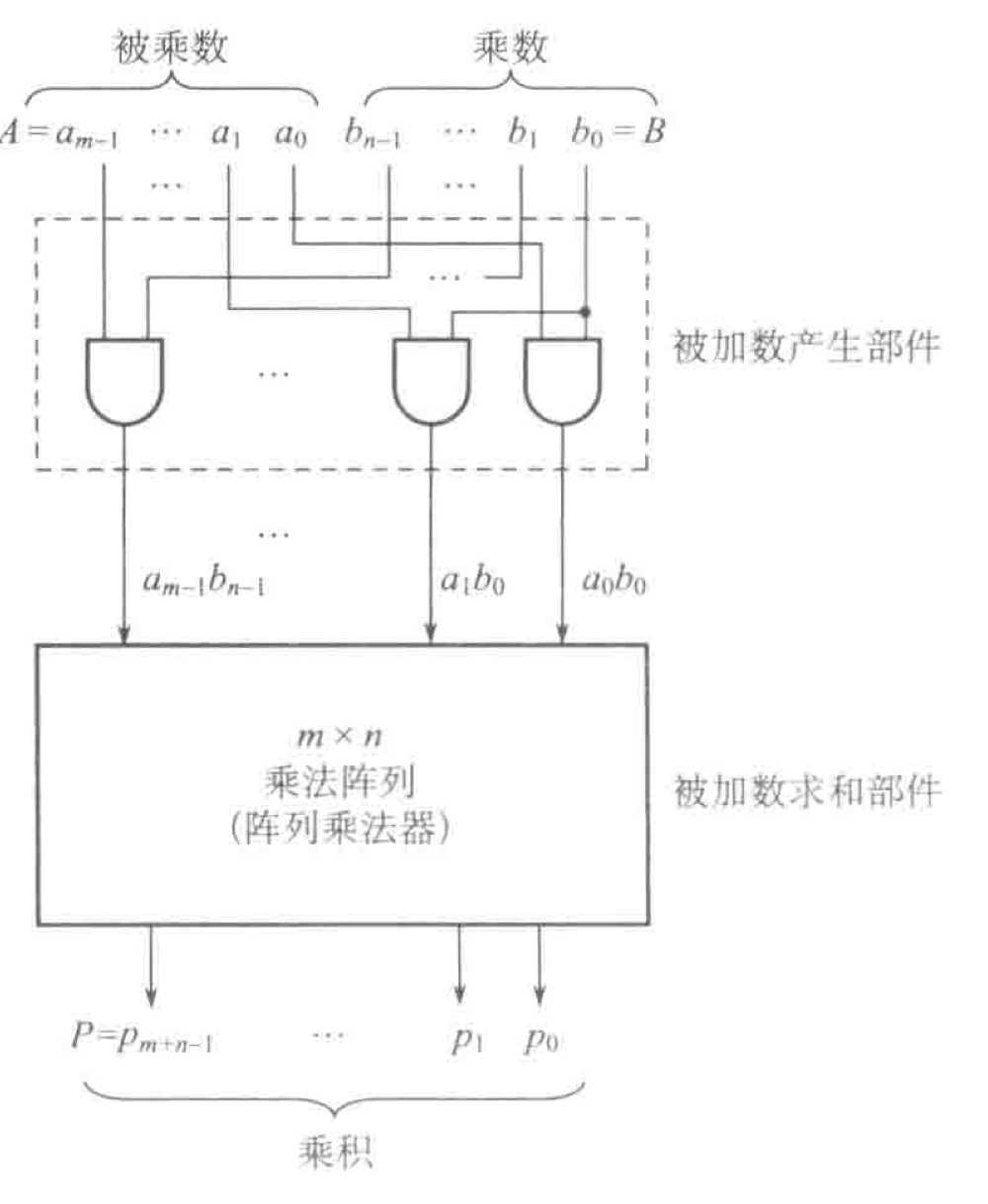
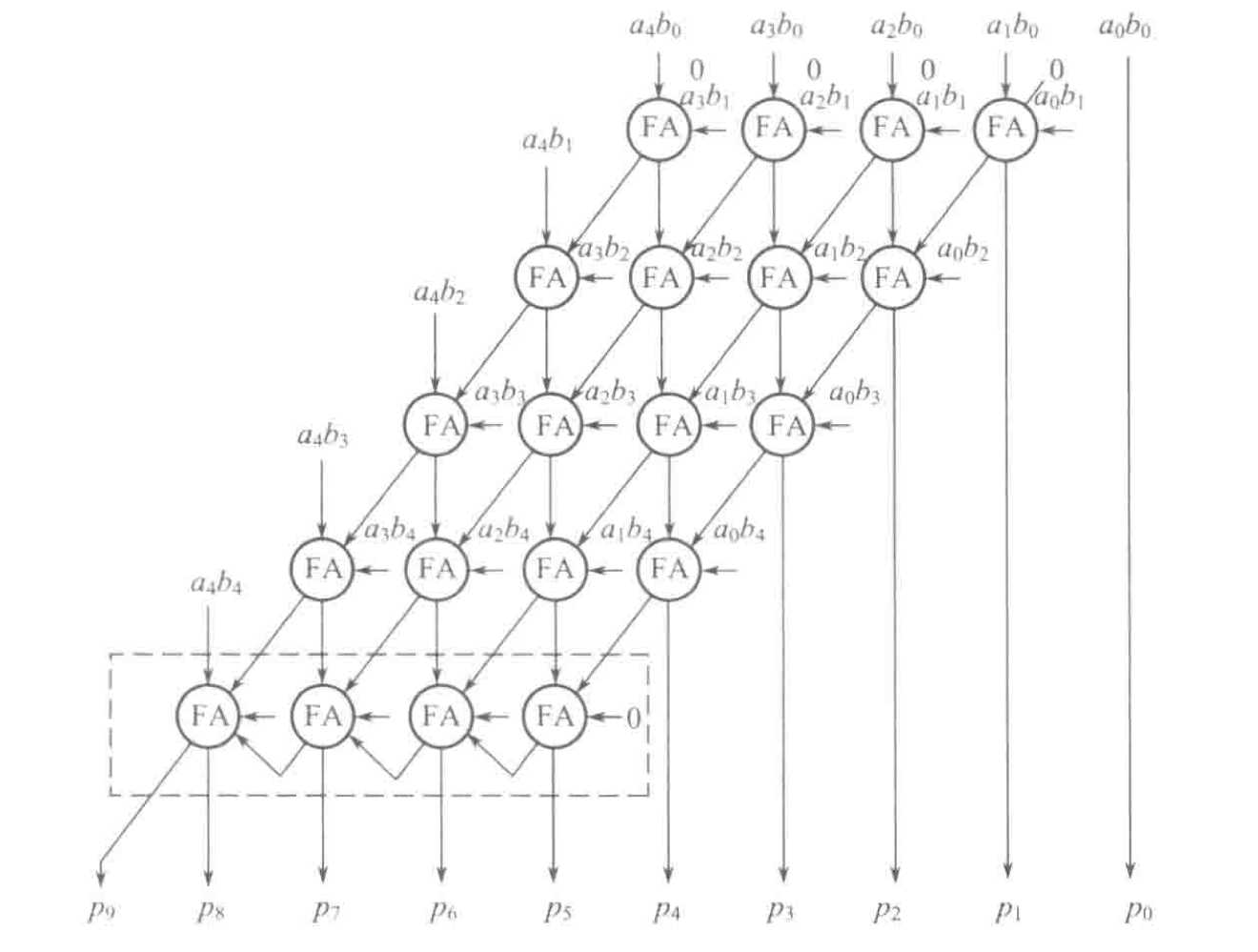
2.3.1 不带符号的列阵乘法器
如图,设$A = a_{m-1}…a_1a_0$ 以及 $B = b_{n-1}…b_1b_0$ ,在二进制的乘法中被乘数 $A$ 和乘数 $B$ 产生 $m+n$ 位乘积 $P = p_{m+n-1}…p_1p_0 = \displaystyle \sum ^ {m-1}_ {i = 0}{\displaystyle \sum^{n-1}_ {j = 0}{(a_ib_j)2^{i+j}}}$,其中每个$a_ib_j$称为一个被加数。
对于$m * n$ 个被加数可以用$m * n$ 个与门并行产生:
产生被加数后需要将其按照上述P的计算公式加起来,可以用一组并行的加法器实现,即列阵乘法器:
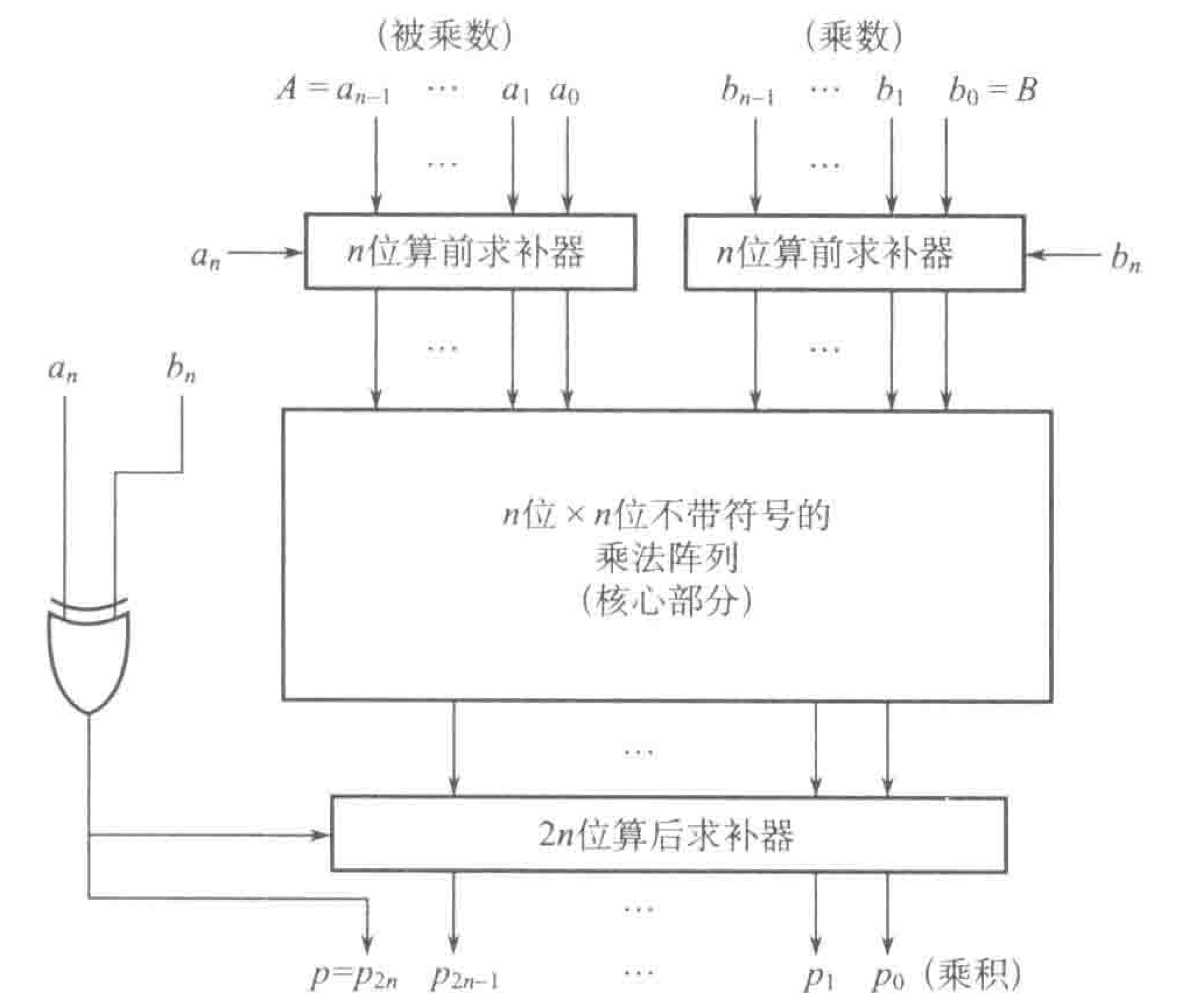
2.3.2 带符号的列阵乘法器
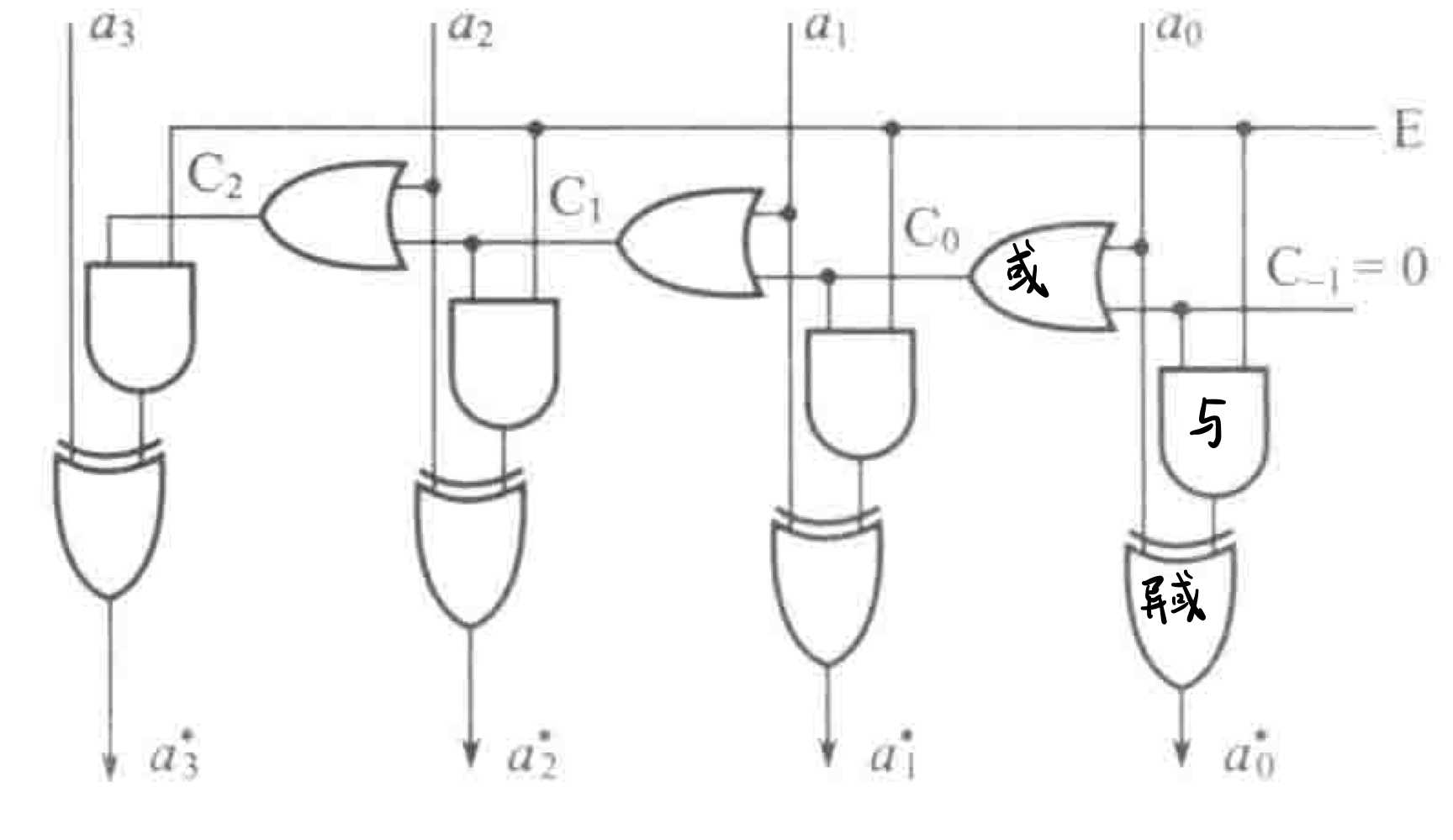
求补方法:从右往左扫描,遇到第一个“1”,将1左边的所有取反,右边连同自己不变,结果就是补码。
如图所示,$C_{-1}$ 始终保持0,$E$ 为控制信号,为1表示进行求补操作。最下方输出的即求补后的结果。
带符号的列阵乘法器含有三个求补器,其中两个为算前求补器,一个位算后求补器,结构如图所示:
使用规则(考):
- 用于原码列阵乘法器:忽略三个求补器,单独考虑符号位,使用原码输入到乘法列阵运算。
-
用于补码列阵乘法器:单独考虑两个乘数的符号位,将负数的数值部分求补后输入给乘法列阵运算,若符号位异或后为1,则将乘法列阵输出的结果求补后加上符号位,如果符号位为0则直接加上符号位。
例题:
1.设x=+15,y=-13,用带求补器的原码阵列乘法器求出乘积x·y
由于是原码列阵乘法器,首先求出x和y的原码:$[ x ]_ 原 = 01111,[ y ]_ 原 = 11101$, 去掉符号位:$|x|=1111,|y|=1101$, 符号位运算:$0 \bigoplus 1 = 1$。
1 1 1 1
× 1 1 0 1
———————————————————
1 1 1 1
0 0 0 0
1 1 1 1
+ 1 1 1 1
———————————————————
1 1 0 0 0 0 1 1
乘积符号为1,算后求补器输出11000011,$[x * y]原=111000011$,换算成二进制数真值是:
$x*y = (-11000011)_2 = (-195)_{10}$。
2.设x=-15,y=-13,用带求补器的补码阵列乘法器求出乘积x·y。
补码列阵乘法器,求出补码$[ x ]_ 补=10001,[ y ]_ 补=10011$,乘积符号位运算:$1 \bigoplus 1=0$。
忽略符号位后用算前求补器输出 $|x|=1111,|y|=1101$ 。
1 1 1 1
× 1 1 0 1
———————————————————————
1 1 1 1
0 0 0 0
1 1 1 1
+ 1 1 1 1
———————————————————————
1 1 0 0 0 0 1 1
乘积符号为0,算后求补器输出 $11000011$,$[x*y]_ 补=011000011$。
补码二进制数真值:
$x * y = 0 * 2^8+1 * 2^7+1 * 2^6+ 1 * 2^1+1 * 2^0 = (+195)_{10}$
十进制数乘法验证:$x * y = (-15) * (-13) = +195$。
2.4 定点除法运算
2.4.1 原码除法算法原理
手算模拟除法:
上图可以发现:人工除法时,人可以比较被除数(余数)和除数的大小来确定商1(够减)或商0(不够减)。
对于机器除法,余数为正表示够减,余数为负表示不够减。不够减时必须恢复原来余数,才能继续向下运算,这种叫做恢复余数法,由于有各种判断和恢复余数的操作,控制较为复杂,不常用。
计算机常用方法:加减交替法
余数为正,商1,下次除数右移做减法;余数为负,商0,下次除数右移做加法。
2.4.2 并行除法器
1. 可控加法减法单元(CAS)
它有四个输出和四个输入端,输入线$P=0$ 时,CAS做加法,$p = 1$ 时,CAS做减法。
CAS的输入输出关系可以用下式表示:
$S_i = A_i \bigoplus(B_i\bigoplus P)\bigoplus C_i$
$C_{i+1} = (A_i + C_i) \bigoplus (B_i \bigoplus P) + A_iC_i$
$P = 1$时:
$S_i = A_i \bigoplus B_i \bigoplus C_i $
$C_{i+1} = A_iB_i + B_iC_i + A_iC_i$
$P = 0$时:
$S_i = A_i \bigoplus \bar{B_i} \bigoplus C_i $
$C_{i+1} = A_i \bar{B_i} + \bar{B_i}C_i + A_iC_i$
2. 加减交替的列阵除法器
3. 例题说明
$x = -0.1011$ $y = -0.1101$, 求$[ x/y ]_ 原$
$[ x ]_ 原 = 1.1011 [ y ]_ 原 = 1.1101 [ y^* ]_ 补 = 0.1101 [ -y^* ]_ 补 = 1.0011 $
2.5 定点运算器的组成
2.5.1 逻辑运算
1. 逻辑非运算
逻辑非也称求反, 对某数进行逻辑非就是按位求反,常用变量上加一横来表示。
$x = x_0x_1x_2…x_n$则 $\bar{x} = \bar{x_0} \bar{x_1} \bar{x_2} … \bar{x_n}$
例:$x_1 = 01001011$ $\bar{x_1} = 10110100$
2. 逻辑加运算
对两个数进行逻辑加就是按位求或,又称为逻辑或,常用“+”表示。
例:$x = 10100001$ $y = 10011011$ $x+y = 10111011$
注意逻辑加是按位运算,所以没有进位!
3.逻辑乘运算
对两个数进行逻辑乘就是按位求与,又称为逻辑与,常用“·”表示。
例:$x = 10111001$ $y = 11110011$ $x·y = 10110001$
注意逻辑乘是按位运算,所以没有进位!
4.逻辑异或运算
对两个数进行逻辑异或就是按位求它们的模2和,又称为按位加,常用“$\bigoplus$”表示。
例:$x = 10101011$ $y = 11001100$ $x\bigoplus y = 01100111$
注意逻辑乘是按位运算,所以没有进位!
2.5.2 多功能算术/逻辑运算单元(ALU)
2.6 浮点运算方法和浮点运算器
2.6.1 浮点加减法
1.浮点加减法规则
2. 运算步骤
0操作数的检查:
检查x和y中是否存在0,如果存在0则无需计算,直接得出答案。
对阶:
将两个浮点数的阶码用补码表示,做相减运算得出需要移动的位数。遵守 小阶向大阶看齐 的原则,即小阶的尾数向右移,每移一位,阶码+1。
尾数加减运算:
与定点加减法运算一样,采用补码运算。
结果规格化:
上图可知:对于补码,规格化要求符号位和第一数位不同。
- 左规
结果是00.00…001…或者11.11…110…这种形式的,没有发生溢出,不断地将尾数相对小数点向左移动一位,阶码相应-1,直到符号位和第一数位不同为止。 - 右规
结果是01.xxxx或10.xxxx时,说明发生溢出,需要向右移动,01.xxxx向右移动一位变成00.xxxx,10.xxxx向右移动一位变成11.xxxx,阶码都相应+1。
舍入操作:
在对阶和右规过程中,可能出现尾数末尾丢失引起误差,需要考虑舍入。
- 0舍1入:类似四舍五入,丢弃的最高位为1,则进1,否则直接舍去。
- 朝0舍入:直接舍去。
- 朝+无穷舍入:正数多余位不全为“0”则进1,负数则截尾。
- 朝-无穷舍入:负数多余位不全为“0”则进1,正数则截尾。
溢出处理:
- 阶码上溢:超出阶码可能表示的最大值的正指数值,一般认为正无穷和负无穷。
- 阶码下溢:超出阶码可能表示的最小值的负指数值,一般认为0。
- 尾数上溢:尾数右移,阶码+1。
- 尾数下溢:尾数右移时最低有效位从尾数域右端流出,需要进行舍入操作。
例子:
$x = 0.11.1 * 2^{10}$ $y = 0.1011 * 2 ^{01}$,求 $x + y$ (除阶符、数符外,阶码取3位,尾数取6位)
解:
$[ x ]_ 补 = 00,010; 00.110100$
$[ y ]_ 补 = 00,001; 00.101100$
- 对阶
- 尾数求和
- 右规