一、神经网络的代价函数

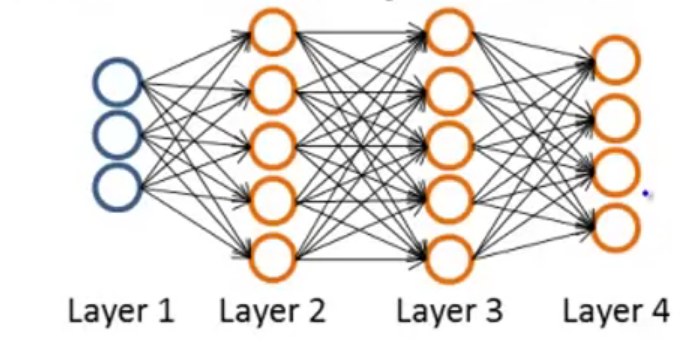
符号定义：

• 假设我们有训练集：$\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\}$
• $x^{(i)}_j$ 表示训练集中第 $i$ 个数据的第 $j$ 个属性值
• 设 $L$ 表示神经网络的总层数，对于上图来说， $L = 4$
• 设 $s_l$ 表示第 $l$ 层的神经元个数（不包括偏置单元），对于上图，$s_1 = 3, s_4 = s_L = 4$
• 对于一个 $K$ 类的分类问题，神经网络模型的输出层就有 $K$ 个单元，即$s_L = K$，用一个列向量 $y \in \mathbb{R}^{K}$ 表示输出的结果。

在Logistic回归中，代价函数为 $J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$，但是在神经网络中输出单元为 $K$ 个，

所以对于神经网络，它的代价函数为：$\begin{gather*} J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2\end{gather*}$，比较我们可以发现，其实就是增加了一些嵌套的求和符号，因为代价函数最终为一个标量，所以我们需要将 $K$ 个输出单元的值相加，对于正则化参数也是如此。

一些说明：关于公式中的 $h_\theta$ ，在神经网络中，只有最后一层输出层所使用的函数能称为 $h_\theta$ ，即假设函数，其公式为 $h_{\theta}(x) = g(\Theta^{(3)}a^{(3)}) = a^{(4)}$ ，这里的 $a^{(i)}$ 为一个列向量，表示第 $i$ 层神经元的激活值，$\Theta^{(3)}$ 表示第 3 层连向第 4 层的权值，为一个矩阵，从这里我们可以看出，在神经网络中，假设函数只是输出层的特殊称谓，实际上，每一层神经元都会使用一次假设函数得到假设值传给下一层神经元。

二、反向传播算法（BP）

2.1 算法介绍

反向传播算法（Backpropagation Algorithm），又称为误差逆传播算法，使用这个算法，使得神经网络模型可以自主地计算出合适的模型参数 $\Theta$，使得模型收敛到一个可能的最优解中。下面来简单介绍一下这个算法。

我们已知代价函数 $J(\Theta)$ ，那么训练目标就是 $\underset{\Theta}{\min} J(\Theta)$，结合梯度下降的思想，我们很容易地想到，就是要求出代价函数对于每个模型权重 $\Theta^{(l)}_{ij}$ 的梯度，即求解 $\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)$ ，其中$\Theta^{(l)}_{ij}$ 表示第 $l+1$ 层的第 $i$ 个神经元和第 $l$ 层的第 $j$ 个神经元之间的权重。

2.2 前向传播

在模型最初的时候，要先进行一次前向传播（Forward propagation），以此获得每个节点的原始激活值。

假设我们只有一个训练样本 $(x,y)$ ，则公式步骤如下：

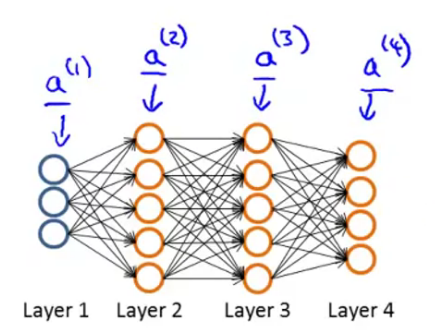
2.3 反向传播

在BP算法中我们首先要计算 $\delta_{j}^{(l)}$ ,它表示第 $l$ 层的第 $j$ 个神经元的误差，注意和前向传播不同的是，反向传播是从输出层向左逐层计算的。以上图中的神经网络模型为例，我们直接给出计算公式（先不必纠结如何得来的公式）：

由于 Sigmoid 函数有个很好的性质：$f^{\prime}(x) = f(x)(1-f(x))$ ，所以就有 $\delta^{(l)}=\left(\left(\Theta^{(l)}\right)^{T} \delta^{(l+1)}\right) \cdot * a^{(l)} \cdot *\left(1-a^{(l)}\right)$，通过一些数学证明，我们可以得到：$\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta) = a^{(l)}_j\delta^{(l+1)}_i$，需要注意的是，这里的等式是忽略掉正则项的。

于是我们得到算法流程：

假设我们有训练集 $\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})\}$

• 先令所有的 $\Delta^{(l)}_{ij} = 0$，这里的 $\Delta$ 其实就是大写的 $\delta$， 用于计算代价函数的偏导数

• For $i = 1$ to $m$

  将 $a^{(1)}$ 赋值成 $x^{(i)}$

  使用前向传播从左向右逐层计算所有的 $a^{(l)}$

  使用 $y^{(i)}$ 计算 $\delta^{(L)} = a^{(L)} - y^{(i)}$

  从右往左逐步计算 $\delta^{(L-1)} \ \ \delta^{(L-2)} \ \ , ..., \delta^{(2)}$

  $\Delta^{(l)}_{ij} := \Delta^{(l)}_{ij}+a^{(l)}_j\delta^{(l+1)}_i$，或者写成向量化 $\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}\left(a^{(l)}\right)^{T}$

• 最终我们可以得到： $\begin{aligned} D_{i, j}^{(l)} &:=\frac{1}{m}\left(\Delta_{i, j}^{(l)}+\lambda \Theta_{i, j}^{(l)}\right), \text { if j } \neq 0 . \\ D_{i, j}^{(l)} &:=\frac{1}{m} \Delta_{i, j}^{(l)} \text { If } \mathrm{j}=0 \end{aligned}$，且 $\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}$

三、MATLAB编程实现

3.1 矩阵向量化

回忆前面的Logistic回归的实现方法，我们利用了一个MATLAB中内置的优化算法 fminunc 来实现自动计算梯度，函数参数如下：

function [jVal, gradient] = costFunction(theta)
optTheta = fminunc(@costFunction, initialTheta, options)

其中 @costFunction 是我们所实现的损失函数的指针，损失函数的输入为 $\theta$ ，输出为计算得到的代价值 jVa;l 以及梯度值gradient ，initialTheta 为初始的 $\theta$ 值，options 为函数的可选项，这里用不到，返回的 optTheta 是进行梯度下降后的 $\theta$ 值。但问题是，这里无论输入还是输出 $\theta$ ，以及代价函数的 gradient 都是一个一维的列向量，而在神经网络中，这些参数都是一个个矩阵，所以我们首先需要进行矩阵的展开。

假设我们有一个三层的神经网络模型，其中第一层神经元个数 $s_1 = 10$ ，$s_2 = 10$， $s_3 = 1$，则有：

在MATLAB中可以用 (:) 的方法将一个矩阵展开成一个向量，具体可以见：机器学习：MATLAB语法 2.2 操作数据

于是我们可以：

thetaVec = [Theta1(:); Theta2(:); Theta3(:)];
Dvec = [D1(:); D2(:); D3(:)];

分别将 $\Theta^{(1)} \ \Theta^{(2)} \ \Theta^{(3)}$ 存入 thetaVec 中，并将 $D_1 \ D_2 \ D_3$ 存入 Dvec 中。

同时我们可以使用：

Theta1 = reshape(thetaVec(1:110), 10, 11);
Theta2 = reshape(thetaVec(111:220), 10, 11);
Theta3 = reshape(thetaVec(221:231), 1, 11);

将 $\Theta^{(1)} \ \Theta^{(2)} \ \Theta^{(3)}$ 从 thetaVec 中恢复回来，$D_1 \ D_2 \ D_3$ 也同理。

那么整体的流程就变成下面这样了：

• 得到初始化后的参数值 $\Theta^{(1)} \ \Theta^{(2)} \ \Theta^{(3)}$

• 将参数展开得到 initialTheta

• 运行函数 fminunc(@costFunction, initialTheta, options) 进行梯度下降

  对于function [jVal, gradientVec] = costFunction(thetaVec)：

  • 从 thetaVec 中使用 reshape 提取出 $\Theta^{(1)} \ \Theta^{(2)} \ \Theta^{(3)}$
  • 使用前向传播和反向传播算法计算 $D_1 \ D_2 \ D_3$ 和 $J(\Theta)$
  • 将 $D_1 \ D_2 \ D_3$ 展开成向量存入 gradientVec

3.2 梯度检验

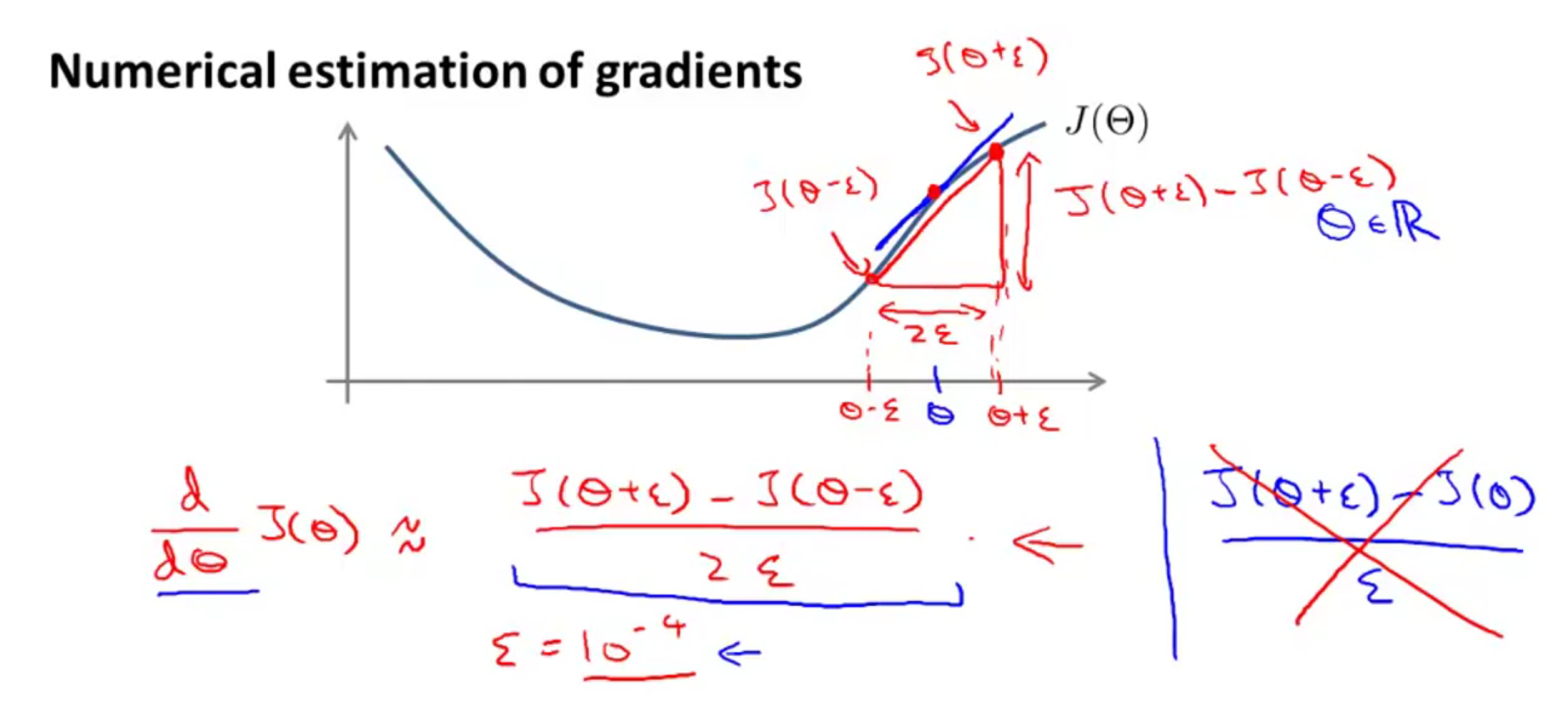
有时候可能由于一些玄学问题导致梯度计算错误，但是你却很难发现，这里介绍了一种检测方法：

如上图所示，假设我们的 $J(\Theta)$ 函数图像是一条这样的曲线，我们可以近似估算 $\frac{d}{d \theta} J(\theta) \approx \frac{J(\theta+\varepsilon)-J(\theta-\varepsilon)}{2 \varepsilon}$，其中 $\varepsilon = 10^{-4}$

由于神经网络的 $\Theta$ 是多个矩阵，所以我们要展开后再进行检测，具体如下：

对应的代码如下：

epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

然后将计算得到的 gradApprox 与反向传播得到的梯度值 gradientVec 逐一比较，如果误差不大则说明没错。

需要注意的是，梯度检测步骤只在模型训练开始前进行一次，开始训练模型后就不用检测了，不然会很慢。

3.3 随机初始化

在线性回归中我们可以将参数初始为0，但是在神经网络中不行，因为如果初始化为0，则最后无论如何进行，最终的参数都是相同的，所以我们需要用一种更加科学的方式进行参数初始化，代码如下：

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

其中 INIT_EPSILON 为自己设置的值。

3.4 其他注意点

• 神经网络的输入层和输出层神经元个数取决于数据的属性个数以及分类个数
• 一般来说，神经网络设置为三层，如果大于三层，则中间的隐藏层的神经元个数都一样多，如果不考虑计算复杂度的问题，神经元个数越多越好，一般比输入的特征数目稍大一点。

3.6 总结流程

1. 随机初始化参数
2. 实现前向传播算法，对于所有的 $x^{(i)}$ 计算得到 $h_{\theta}(x^{(i)})$
3. 实现代价函数
4. 实现反向传播算法，计算偏导数 $\frac{\partial}{\partial \Theta_{j k}^{(l)}} J(\Theta)$
5. 进行梯度检验（只在一开的时候进行一次）
6. 使用梯度下降或者其他高级的优化算法来更新参数以最小化代价函数