终于到动态规划了,最难的DP书上居然就7面的详解(可能教学大纲只是为了入门吧),一开始学的时候确实头大,现在也只能说半只脚踏入DP大门,本章可能讲的不是很好欢迎提出意见!下面稍微介绍一下动态规划吧
动态规划
引自维基百科
动态规划(英语:Dynamic programming,简称DP)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
动态规划问题最重要的是学会拆分问题,而拆分问题靠的是定义状态和写出状态转移方程。
下面以POJ1163题为例:原题直通车
在下面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可,不必给出具体路径。 三角形的行数n大于1小于等于100,数字为 0 – 99
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
一般思路:
首先我们用一个二维数字a[x][y]来存数字三角形,x表示行,y表示列(xy从1开始算起),然后我们用ans[x][y]来表示点(x,y)到底部的最佳路径,问题就变成求ans[1][1]了,那么首先我们可以想到递归的做法——每次只能向下或者向右下走,点(x,y)出发下一步必然是(x+1,y)或者(x+1,y+1),所以(x,y)到底部的最优路径一定是(x+1,y)或者(x+1,y+1)到底部最优路径加上a[x][y],那么我们可以得到如下递归方程:
int digui(int x,int y)
{
if(x==n)//递归边界,最底下一层到底部的最优就是自己
ans[x][y]=a[x][y];
else
ans[x][y]=max(digui(x+1,y),digui(x+1,y+1))+a[x][y];
}
优化一下:
恭喜你这道难题被你轻松的解决了
如果你就这样兴高采烈的交上去一定会收到一个大大的TLE(超时),原因在于这样递归,程序会有很多次重复计算,时间复杂度2^n^
那该怎么办呢??这时你的脑子里应该闪现出一个灵感,为什么我不能把每次计算的答案存下来,如果再次需要的时候直接拿来用就行了呀
没错,聪明的你就是用到了动态规划的思想~
根据这个思路我们优化代码得到:
int digui(int x,int y)
{
if(ans[x][y]!=-1) return ans[x][y];//每次现查询这个答案是否计算过,减少计算次数,ans初始化为-1
if(x==n)//递归边界,最底下一层到底部的最优就是自己
ans[x][y]=a[x][y];
else
ans[x][y]=max(digui(x+1,y),digui(x+1,y+1))+a[x][y];
}
由于三角形总数为n(n+1)/2,所以以上代码的时间复杂度为n^2^,比原来的2^n^ 优化了不少,代码提交也能AC了
还能更好:
但你以为这就是最好的了?程序员要争做最棒的男人!
递归不断的调用函数,如果n过大会造成爆栈(不理解为什么爆栈的点这里),我们可以把递归转换成递推式:
首先我们计算最后一行的ans,不要想也知道最后一行的ans等于最后一行的a:
4 5 2 6 5
那么开始分析倒数第二行,第二行的第一个ans可以是2+4也可以是2+5,取最大2+5=7,第二个ans可以是7+5||7+2,取7+5,由此可得:
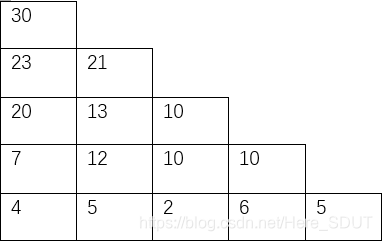
由此我们可以写出代码:
for(int i=1;i<=n;i++)
ans[n][i]=a[n][i];
for(int i=n-1;i>=1;i--)
for(int j=1;j<=i;j++)
ans[i][j]=max(ans[i+1][j],ans[i+1][j+1])+a[i][j];
值得一提的是这个代码在空间复杂度上还能优化,利用滚动数组可以把ans用一维数组表示,这里不详细展开。
小结:
回顾我们刚才解决问题的过程可以得到DP问题的一般解决思路:
- 重新定义问题,找到状态
> 原问题:找到从顶点到底部的最优路线
> 重新定义:给定一个数字三角形有n行,设ans[x][y]为点(x,y)到底部的最优路径,求ans[1][1]
这里的所有ans[x][y]就是这个问题的所有状态,设ans[x][y]为点(x,y)到底部的最优路径就是对状态的定义,一共有n(n+1)/2个。
- 找到状态转移方程
定义:上述状态定义好之后,状态和状态之间的关系式,就叫做状态转移方程。数字三角形中的状态转移方程就是:
ans[n][y]=a[n][y];(根据状态定义确定一些初始状态(边界状态)的值)
ans[x][y]=max(ans[[x+1][y],ans[x+1][y+1])+a[x][y];
状态转移方程,就是定义了问题和子问题之间的关系。可以看出,状态转移方程就是带有条件的递推式。
能用动规解决的问题的特点:
- 问题具有最优子结构性质。如果问题的最优解所包含的 子问题的解也是最优的,我们就称该问题具有最优子结 构性质。
- 无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
参考博客:
教你彻底学会动态规划——入门篇
动态规划(DP)通俗讲解
SDUTOJ题解
6-1递归的函数
#include <stdio.h>
#include <stdlib.h>
int dp[31][31][31];
int f(int a,int b,int c)
{
if(a<=0||b<=0||c<=0)
return 1;
if(dp[a][b][c]>0) return dp[a][b][c];
else if(a>20||b>20||c>20)
return dp[a][b][c]=f(20,20,20);
else if(a<b&&b<c)
return dp[a][b][c]=f(a,b,c-1)+f(a,b-1,c-1)-f(a,b-1,c);
else
return dp[a][b][c]=f(a-1,b,c)+f(a-1,b-1,c)+f(a-1,b,c-1)-f(a-1,b-1,c-1);
}
int main()
{
int a,b,c;
while(~scanf("%d %d %d",&a,&b,&c))
{
printf("%d\n",f(a,b,c));
}
return 0;
}
6-2数字三角形问题
#include <stdio.h>
#include <stdlib.h>
int max(int a,int b)
{
return a>b ? a : b;
}
int a[101][101];
int ans[101][101];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
scanf("%d",&a[i][j]);
}
for(int i=1; i<=n; i++)
ans[n][i]=a[n][i];
for(int i=n-1; i>=1; i--)
for(int j=1; j<=i; j++)
ans[i][j]=max(ans[i+1][j],ans[i+1][j+1])+a[i][j];
printf("%d\n",ans[1][1]);
return 0;
}
6-3小鑫去爬山
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int min(int a,int b)
{
return a<b ? a : b;
}
int Inf=0x7fffffff;//int范围内最大值
int a[101][101];
int ans[101][101];
int main()
{
int n;
while(~scanf("%d",&n))
{
memset(ans,Inf,sizeof(ans));
for(int i=1; i<=n; i++)
{
for(int j=1; j<=i; j++)
scanf("%d",&a[i][j]);
}
for(int i=1; i<=n; i++)
ans[n][i]=a[n][i];
for(int i=n-1; i>=1; i--)
for(int j=1; j<=i; j++)
ans[i][j]=min(ans[i+1][j],ans[i+1][j+1])+a[i][j];
printf("%d\n",ans[1][1]);
}
return 0;
}
6-4最长公共子序列问题
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int max(int a,int b)
{
return a>b? a:b;
}
int main()
{
char s1[501],s2[502];
int len1,len2,dp[501][501];
while(~scanf("%s %s",s1,s2))
{
len1=strlen(s1);
len2=strlen(s2);
for(int i=0;i<=len1;i++)
dp[i][0]=0;
for(int i=0;i<=len2;i++)
dp[0][i]=0;
for(int i=1;i<=len1;i++)
for(int j=1;j<=len2;j++)
if(s1[i-1]==s2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
printf("%d\n",dp[len1][len2]);
}
return 0;
}
6-5最长上升子序列
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int max(int a,int b)
{
return a>b? a:b;
}
int main()
{
int n,a[1010],dp[1010];
scanf("%d",&n);
for(int i=0; i<n; i++)
{
scanf("%d",&a[i]);
dp[0]=1;
}
for(int i=1; i<n; i++)
{
//这里只能是0,其他数字都不行,比0大会导致它不是最小的,比0小会导致如果没找到小于a[i]的数那dp[i]就变成小于1的数,而dp的值最小为1,这里当时没考虑完善
int Max=0;
for(int j=0; j<i; j++)
{
if(a[i]>a[j]&&dp[j]>Max)
Max=dp[j];
}
dp[i]=Max+1;
}
int ans=-1;
for(int i=0; i<n; i++)
ans=max(ans,dp[i]);
printf("%d\n",ans);
return 0;
}
6-6上升子序列
和上题几乎一样
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int max(int a,int b)
{
return a>b? a:b;
}
int main()
{
int n,a[1010],dp[1010];
while(~scanf("%d",&n))
{
for(int i=0; i<n; i++)
{
scanf("%d",&a[i]);
}
dp[0]=a[0];
for(int i=1; i<n; i++)
{
int Max=0;
for(int j=0; j<i; j++)
{
if(a[i]>a[j]&&dp[j]>Max)
Max=dp[j];
}
dp[i]=Max+a[i];
}
int ans=-1;
for(int i=0; i<n; i++)
ans=max(ans,dp[i]);
printf("%d\n",ans);
}
return 0;
}
6-4 pro max 最长公共子序列
这题求多个字符串的最长公共子序列,比6-4的难很多,用到了变维dp的思想,我们知道两个字符串求最长公共子序列问题时使用了一个二维dp来保存所有的状态,但这里是多个字符串,三位数组不太现实,我们可以利用哈希,把多维的状态储存到一维,然后再利用类似于求两个字符串的思想来求——从最后一个字符开始如果所有的字符串的第x个字符都相等,那么这里的值就是x-1个字符对应的最长长度+1,否则就枚举所有情况,具体解释可以看这个博客,讲的比较详细 直通车,考试不做要求,暂不展开,下面放代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
char a[110][110];
int dp[30000 + 10];
int len[110];
int n;
int DP( int *x )//x记录每个字符串的动态长度,即每个状态对应的每个字符串长度,这里需要一定理解,每个状态可以想成把一部分字符串丢掉,即长度减少
{
int i, j, index, ret;
for( i = 1; i <= n; i++ )//如果有一个字符串的长度为0,那么最长公共子序列必定为0
{
if( x[i] == 0 )
{
return 0;
}
}
for( index = x[n] - 1, i = n - 1; i >= 1; i-- )
{
index = index * len[i] + x[i] - 1; //转化为一维数组,这里可以自己推导一下,上面分享的博客里有解释
}
if( dp[index] >= 0 )//如果之前求过这个状态直接返回,减少重复计算,dp的核心思想
{
return dp[index];
}
//从每个字符串的末尾开始匹配
for( i = 2; i <= n; i++ )
{
if( a[1][x[1] - 1] != a[i][x[i] - 1] )
{
break;
}
}
if( i > n )//如果都相等则把字符串长度都-1,答案就行-1后字符串求dp的答案+1
{
for( j = 1; j <= n; j++ )
{
x[j]--;
}
ret = DP(x) + 1;//dp求得长度-1的字符串状态的最长+1
for( j = 1; j <= n; j++ )
{
x[j]++;
}
}
else
{
ret = 0;
int t;
//开始枚举每一种情况,取最大值保留
for( j = 1; j <= n; j++ )
{
x[j]--;
t = DP( x );
ret = max( ret, t );
x[j]++;
}
}
dp[index] = ret;//记忆化
return ret;
}
int main()
{
int T;
int L[110];
scanf("%d", &T);
while( T-- )
{
scanf("%d", &n);
for( int i = 1; i <= n; i++ )
{
scanf("%s",a[i] );
len[i] = L[i] = strlen( a[i] );
}
memset( dp, -1, sizeof(dp) );
printf("%d\n", DP( L ) );
}
return 0;
}
6-8取数字问题
这题用到了深度优先搜索(DFS)和动态规划的知识
这道题的要求是得到正数最小的路径,那么单单一个dp记录一条路是不行的,你需要遍历所有情况,走过所有路才能得到最优情况,dfs就可以满足要求,具体看呆码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int max(int a,int b)
{
return a>b? a:b;
}
int n,m;
int ans=0x3f3f3f3f,mp[11][11];//ans设为int范围的最大值,用于取最正数。
void dfs(int i,int j,int sum)//i,j表示现在在哪个点,sum表示从原点到(i,j)的和
{
sum+=mp[i][j];
if(i<m-1)//如果没到最下边,则继续往下走,i+1表示向下一行的意思
dfs(i+1,j,sum);
if(j<n-1)//如果没到最右边,则继续向右走
dfs(i,j+1,sum);
if(i==m-1&&j==n-1&&sum>0&&sum<ans)//到达右下角了,判断这条路是否满足正数最小
ans=sum;
}
int main()
{
scanf("%d %d",&m,&n);
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
scanf("%d",&mp[i][j]);
dfs(0,0,0);//从原点开始
if(ans==0x3f3f3f3f)
printf("-1");
else
printf("%d\n",ans);
return 0;
}
6-9免费馅饼
当前状态可以由上一秒的左边位置、右边位置或者原位置变来,所以我们用一个二维坐标dp[t][x]来表示t秒x位置的最多馅饼数,这里我们得从结束时间往前遍历。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int max(int a,int b)
{
return a>b? a:b;
}
int dp[100001][15];
int main()
{
int n;
while(~scanf("%d",&n)&&n)
{
int maxt=0;
memset(dp,0,sizeof(dp));
for(int i=0; i<n; i++)
{
int x,t;
scanf("%d %d",&x,&t);
maxt=max(maxt,t);
dp[t][x]++;
}
for(int i=maxt-1; i>=0; i--)
{
dp[i][0]+=max(dp[i+1][0],dp[i+1][1]);
for(int j=1; j<=10; j++)
{
dp[i][j]+=max(max(dp[i+1][j-1],dp[i+1][j]),dp[i+1][j+1]);
}
}
printf("%d\n",dp[0][5]);
}
return 0;
}
6-10走迷宫
用到了dfs的思想,dfs遍历所有可能,把路径存到结构体数组里,如果可达,则遍历输出
#include<stdio.h>
#include<string.h>
struct node
{
int x, y;
} ls[1000];
int dx[] = {0,-1,0,1}, dy[] = {-1,0,1,0};
int bj[16][16], map[16][16];
int m, n, step, sum = 0, xz, yz;
void dfs(int x1, int y1)
{
int i;
if(x1 == xz && y1 == yz)
{
sum++;
for(i = 0; i < step; i++)
{
printf("(%d,%d)",ls[i].x,ls[i].y);
if(i < step - 1)
printf("->");
}
printf("\n");
}
else
{
int kx, ky;
for(i = 0; i < 4; i++)
{
kx = x1 + dx[i];
ky = y1 + dy[i];
if(kx >= 1 && ky >= 1 && kx <= n && ky <= m && !bj[kx][ky] && map[kx][ky])
{
ls[step].x = kx;
ls[step].y = ky;
step++;
bj[kx][ky] = 1;
dfs(kx,ky);
bj[kx][ky] = 0;
step--;
}
}
}
}
int main()
{
int i, j,xq,yq;
while(~scanf("%d%d",&n,&m))
{
memset(bj,0,sizeof(bj));
memset(ls,0,sizeof(ls));
for(i = 1; i <= n; i++)
for(j = 1; j <= m; j++)
scanf("%d",&map[i][j]);
scanf("%d%d%d%d",&xq,&yq,&xz,&yz);
ls[0].x = xq;
ls[0].y = yq;
sum = 0;
step = 1;
bj[xq][yq] = 1;
dfs(xq,yq);
if(sum == 0)
printf("-1\n");
}
return 0;
}
小结
dp打的我头秃,动态规划确实难的一批,虽然定义简单,原理清晰,但是应用很灵活,状态很难定义,导致状态转移方程不好写,同时还会用到很多别的算法思想考察较为综合,递推递归贪心也在这里有体现,期末考试考察较为入门,只考察到6-6,但是动态规划在编程里还是十分重要的,还有各种很著名的应用比如背包问题,迪杰斯特拉算法求最短路等等,一起加油好好学吧!
