2020.5.27 刚学完二分图感觉总结一下比较好，图论确实让人头秃，差不多一个多星期大概理解了二分图的内容，但还是挺生涩，还是多打点题吧
由于第一次学可能有些地方有出错欢迎大家指正！
2020.8.22 再次和二分图不期而遇，这次学完了二分图最大权匹配、覆盖、独立集的内容，还给别人讲课理解的较为透彻，故决定完善此博客，我也是从小白过来的，明白自学找博客找教学很累，网上的东西参差不齐，所以我尽量用易懂的方式介绍二分图的知识，可能会比较长，希望可以耐心看下去，相信你一定会有所收获的！（码字不易 求赞！）

一、二分图必备概念

1. 二分图的定义

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。（简单说就是把一个图的顶点分成两个集合，且集合内的点不邻接）

2. 匹配

1.匹配：给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
2.极大匹配：指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。
3.最大匹配：所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
4.完全匹配（完备匹配）：一个匹配中，图中的每个顶点都和图中某条边相关联。(最大权匹配会碰到这个概念，mark一下)

二、二分图的判断

1. 理论判断

• 如果某个图为二分图，那么它至少有两个顶点，且其所有回路的长度均为偶数，任何无回路的的图均是二分图（树就是二分图）。

个人理解：两个顶点很好理解，毕竟一个点也不能配对。无回路也可以很容易把点分成两个无关的集合。有回路时，如果回路为奇数
（图2）无论如何不能分成两个无关联的集合，故不是二分图，偶数则可以（图1）。

严谨证明通过反证法，先假设有回路且回路为奇数，最后会发现矛盾。

2. 程序判断（染色法）

• 用两种颜色，对所有顶点逐个染色，且相邻顶点染不同的颜色，如果发现相邻顶点染了同一种颜色，就认为此图不为二分图。
  当所有顶点都被染色，且没有发现同色的相邻顶点，就退出，此图是二分图。

  个人理解：其实和理论判断的原理是一样的，巧妙地将回路的奇偶转换成颜色的异同。另外，需要注意的是，若没说明是连通图，需要遍历全部顶点。

  染色法不一定只能用来判断二分图，还可以顺便用来建二分图，题目给你的图一般不会给你分好左右部，此时你就可以通过染色找出左右部，当然一些图还有其他的建图办法后面会提到。

下面用邻接表法分别给出dfs和bfs的代码

bfs法

const int maxn = 1e5+10;
vector <int> G[maxn];
int col[maxn];
bool bfs(int u)//这里因为不一定连通图的原因设置一个变量，外部引用函数的时候遍历访问就行
{
    queue<int> q;
    q.push(u);//当前点入队
    col[u]=1;//当前点涂色
    while(!q.empty())
    {
        int v=q.front();
        q.pop();
        for(int i=0;i<G[v].size();i++)//遍历与当前点关联的所有点
        {
            int x=G[v][i];//获得第i个关联点的下标
            if(col[x]==0)//如果没图色
            {
                col[x]=-col[v];//图相反颜色
                q.push(x);
            }
            else
            {
                if(col[x]==col[v])//颜色相同不是二分图返回false
                    return false;
            }
        }
    }
    return true;
}

void solve()
{
    for(int i=1;i<=n;i++)
    {
       if(col[i]==0&&!bfs(i))
       {
           printf("No\n");
           return;
       }
    }
    printf("Yes\n");
}

dfs法

bool dfs(int v, int c){
    color[v] = c;    //将当前顶点涂色
    for(int i = 0; i < n; i++){    //遍历所有相邻顶点，即连着的点
        if(edge[v][i] == 1){    //如果顶点存在
            if(color[i] == c)    //如果颜色重复，就返回false
                return false;
            if(color[i] == 0 && !dfs(i,-c))    //如果还未涂色，就染上相反的颜色-c,并dfs这个顶点，进入下一层
                return false;   //返回false
        }
    }
    return true;   //如果所有顶点涂完色，并且没有出现同色的相邻顶点，就返回true
}

三、最大匹配

1. 概念

• 交替路：从一个未匹配的点出发，依次经过未匹配边、匹配边、未匹配边….这样的路叫做交替路。
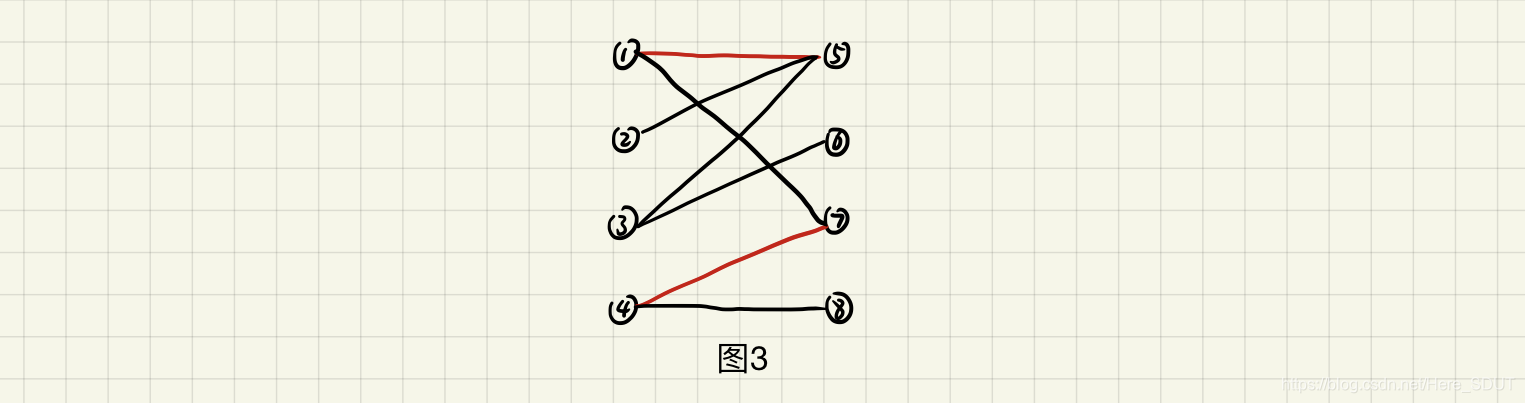
• 增广路：从一个未匹配的点出发，走交替路，到达了一个未匹配过的点，这条路叫做增广路（图3）。
  
  

红线代表匹配边， 1、5、4、7已匹配，则8->4->7->1->5为一条增广路

2. 匈牙利算法

• 原理：匈牙利算法通过不断求增广路来求最大匹配。因为增广路有下面四个性质：

  1.增广路有奇数条边 。
  2.路径上的点一定是一个在X边，一个在Y边，交错出现。
  3.起点和终点都是目前还没有配对的点。
  4.未匹配边的数量比匹配边的数量多1。
  主要是性质4，由于未匹配边数量比匹配边多1，故只要有增广路那么把这条路的匹配边变成未匹配边，未匹配边变成匹配边那么总匹配边数就能加1。
  贴上一个生动形象的博客：四个男人和四个女人的故事

• 代码

const int maxn = 1e5+10;

vector <int> G[maxn];
int n,m;//n为点的数量 m为边的数量
int vis[maxn],pei[maxn];//vis记录点是否被访问，pei存每个点所匹配的点

bool dfs(int u)
{
    for(int i=0;i<G[u].size();i++)//遍历与该点关联的所有点
    {
        int v=G[u][i];//所关联的点
        if(!vis[v])//没访问过
        {
            vis[v]=1;
            if(!pei[v]||dfs(pei[v]))//若关联的点没被匹配或者dfs返回true说明关联的点所匹配的点可以挪走，则把关联的点和传入的点匹配（即下面代码）
            {
                pei[v]=u;
                return true;
            }
        }
    }
    return false;
}

void solve()
{
    int ans=0;
    for(int i=1;i<=n;i++)//遍历所有的点
    {
        memset(vis,0,sizeof(vis));
        if(dfs(i)) ans++;//如果有增广路则加一条匹配边
    }
    printf("%d\n",ans);
}

3. 例题

Fire Net HDU – 1045 这题还用到了缩点的原理 需要思考一下
The Accomodation of Students HDU – 2444 很裸的判断二分图+最大匹配

四、最大权匹配

1. 定义

给定一张二分图，每条边都有一个权值。求出该二分图的一组最大匹配，使得匹配边的权值总和最大。

2. 概念定义

• 交错树：匈牙利算法中，从某个左部节点出发寻找匹配失败，那么在dfs过程中，所有访问过的节点，以及为了访问这些节点而经过的边，共同构成一棵树。这棵树的根是一个左部节点，所有叶子节点也都是左部节点（因为最终匹配失败了），并且树上第1、2、3…层都是非匹配边，第2、4、6…为匹配边。
• 顶标：全称“顶点标记值”。在二分图中给第i个左部节点一个整数值A~i~，第j个右部节点一个整数值B~j~（1<=i,j<=n），满足对于i，j间任意的一条边，边权值小于等于A~i~+B~j~，一般我们将左部点顶标值设为该点所有边的最大边权值，右部点顶标设为0，这样一定满足要求。
• 相等子图：带权二分图中满足边权=两端点顶标和的所有边构成的一个子图。

3. 定理

若相等子图中存在完备匹配，则这个完备匹配呼吁事故二分图的带权最大匹配。（KM算法的缺陷，只能求存在完备匹配的最大权匹配）

证明：
1.由于完备匹配包含二分图中所有的节点，根据相等子图的定义，这个完备匹配的边权之和等于所有顶标和
2.假设还有一个完备匹配，此完备匹配不完全等于相等子图，对于不在相等子图中的边，边权值一定小于两端点的顶标和，所有这个完备匹配的边权之和必定小于相等子图中的完备匹配，故相等子图中的完备匹配最大。

4. 程序实现（KM算法）

• 图解模拟《国家分配女友》
  背景：在男女比例失衡的23世纪，中华大地上广大男同胞们面临了一个严峻的问题——母胎solo多年找不到女朋友，考虑到广大男同胞们的幸福和人类文明的传承，国家开始推行“计划女友”，规定如下：男孩和女孩只能一对一，男孩女孩都不能脚踏两条船。只有相互有好感的男女之间才能相互配对。由于女少男多，女生有选择权，每个女生有一个期望值，该期望值为他有好感的男生中最大的好感度，男生没有期望值 为什么？没本事需要国家分配还想挑三拣四？给爷爪巴，为了在一起后能幸福，规定只有男女好感之和等于双方期望值的才能进行分配（大于也不行，别问反正就是不行），为了双方的幸福和人类文明的延续，国家希望在分配尽量多的前提下，保证所有情侣好感度之和最大。（以上内容纯属瞎编，如有雷同……别做梦了铁子，勇敢点，别想着国家真能给你分配）
  1.1是三男三女之间的关系，希望求出最优的分配方法。
  
  
  • 1.1 我们按照女生从上到下依次分配，先给女一分，发现和男三可以配对。
  • 1.2给女二分配，发现满足条件的只有男三，但是男三已经有女一了，那么我们询问女一能不能换一个男友，可惜女一没有别的合适对象，匹配失败。
  • 1.3 为了产生尽量多的情侣，只能牺牲一下女一和女二了，让她们降低一下期望值，至于降低多少，首先我们明确降低期望的目的是增加情侣，所以我们寻找女一和女二有好感度的且没有在这次匹配中被访问过的所有男生，找到降低最少的值，（女一连男一要降1，女二连男一降低1，女二连男二降低2，取三个的最小值即1），又由于男三被两个女生抢，所以自信心爆棚，他的期望也相应+1（女生降多少男生就加多少）
  • 1.4 再次分配，其实也能看出来分配的过程就是走增广路，如果有增广路那么就能让匹配数+1，如图粉红色的路为增广路。
  • 1.5找到增广路后取反，即将匹配边变为非匹配边，非匹配边变为匹配边，这样可以让匹配数+1，如图女一女二完成了匹配，然后给女三匹配，发现女三无法匹配任何人（男三由于期望+1了所以不满足条件）
  • 1.6将女三的期望减低1让她可以和男三匹配，寻找增广路（粉色），发现寻找失败。
  • 1.7由于增广匹配失败，那么就要降低参与匹配的女生的期望，同时参与匹配的男生期望会相应增加，我们发现，只有女二所对应的男二没有被访问到，相应期望的改变值为1，所以参与匹配的所有女生期望-1，男生期望+1，然后走增广路（粉色）发现找到一条增广路。
  • 1.8 增广路进行取反操作，完成匹配。
  • 很容易发现，这里的期望值就是顶标的定义，好感度就是边权，分配女友计划实际就是二分图最大权匹配。
  • 程序化图解流程：
  • 顶标初始化：遍历每个左部点的所有边，找到边权最大的赋为左部点的顶标值，右部点全部初始化为0
  • 寻找完备匹配：类匈牙利算法，每个左部点跑一遍增广路，都找到了增广路则找到了二分图的完备匹配，增广失败进入下一步
  • 扩大相等子图：增广失败时，我们需要考虑扩大相等子图来继续找增广路（由于完备匹配一定存在，所有一定可以找到增广路）。扩大相等子图的方法是修改交错树中的顶标值，对于左部点+d，右部点-d，d以下操作获得：访问所有交错树中的左部点相连的不在交错树中的右部点，对于每条这样的边找到顶标和减去边权值的最小值作为d（描述的有点绕可结合图片模拟过程理解）。
• KM模板

#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define LL long long
using namespace std;
const int maxn = 1e3+10;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;

int wx[maxn], wy[maxn];  //每个点的顶标值（需要根据二分图处理出来）
int matchx[maxn], matchy[maxn];        //每个点所匹配的点
int visx[maxn], visy[maxn];    //每个点是否加入增广路
int cntx = maxn, cnty = maxn;  //分别是X和Y的点数
int mp[maxn][maxn];  //二分图边的权值
int d;  //边权和顶标最小的差值

bool dfs(int u)  //进入DFS的都是X部的点
{
    visx[u] = 1;  //标记进入增广路
    for (int v = 0; v < cnty; v++) {
        if (!visy[v] && mp[u][v] != INF)
        {
            int t = wx[u] + wy[v] - mp[u][v];
            if (t == 0)  // t为0说明是相等子图
            {
                visy[v] = 1;
                if (matchy[v] == -1 || dfs(matchy[v])) {
                    matchx[u] = v;
                    matchy[v] = u;  //进行匹配
                    return true;
                }
            } 
            else if (t > 0)  //此处t一定是大于0，因为顶标之和一定>=边权
            {
                d = min(d, t);  //边权和顶标最小的差值
            }
        }
    }
    return false;
}

int KM() {
    memset(matchx, -1, sizeof(matchx));
    memset(matchy, -1, sizeof(matchy));
    memset(wx, 0, sizeof(wx));  // wx的顶标为该点连接的边的最大权值
    memset(wy, 0, sizeof(wy));      // wy的顶标为0
    for (int i = 0; i < cntx; i++)  //预处理出顶标值
    {
        for (int j = 0; j < cnty; j++) {
            if (mp[i][j] == INF) {
                continue;
            }
            wx[i] = max(wx[i], mp[i][j]);
        }
    }
    for (int i = 0; i < cntx; i++)  //枚举X部的点
    {
        while (1) {
            d = INF;
            memset(visx, 0, sizeof(visx));
            memset(visy, 0, sizeof(visy));
            if (dfs(i)) break;  //已经匹配正确

            //还未匹配，将X部的顶标减去d，Y部的顶标加上d
            for (int j = 0; j < cntx; j++)
                if (visx[j]) wx[j] -= d;
            for (int j = 0; j < cnty; j++)
                if (visy[j]) wy[j] += d;
        }
    }

    int ans = 0;  //二分图最优匹配权值
    for (int i = 0; i < cntx; i++)
        if (matchx[i] != -1) ans += mp[i][matchx[i]];
    return ans;
}
int n, k;
int main() {
    int result = KM();
    cout << result << endl;
    return 0;
}

五、覆盖和独立集

1.最小点覆盖

• 定义：给定一张二分图，求出一个最小的点集S，使得图中任意一条边都有至少一个端点属于S。
• Konig定理：二分图最小点覆盖包含的点数等于二分图最大匹配包含的边数。
• 证明：
  • 最小点覆盖>=最大匹配数：根据匹配的定义，一组匹配中无交点，那么要覆盖住所有的边，如果有m个匹配那么就至少m个点
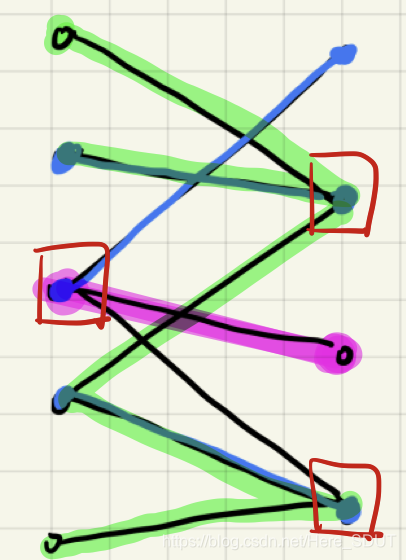
  • 最小点覆盖<=最大匹配数：构造法，如图：
  
  蓝色线代表该二分图的最大匹配，我们从左部所有的非匹配点出发，做一个增广路（必定失败，因为已经存在最大匹配了），标记经过的所有点（绿色为所有的左部非匹配点出发的增广路径），我们选取左边所有未被标记的点和右边所有被标记的点（红色方框），这几个点就是该二分图的一个覆盖，理由如下：
  首先明确几个此构造的性质：

• 性质1.左部所有非匹配点都被标记（因为从左部非匹配点出发肯定都被标记）。
• 性质2.右部所有非匹配点一定未被标记（反证法，如果有右边非匹配点被标记了，说明有一条增广路走到了右部的一个非匹配点，找到一条增广路，与最大匹配矛盾）。
• 性质3. 每个匹配边左右两点同时被标记或同时未被标记（从图中可以看出，匹配边可以分为两类，一类匹配边的右部点存在一条边连向左部的一个非匹配点，那么肯定两个点都被标记，还有一种就都不被标记，看图找一找就知道了）

二分图的边可以分为匹配边和非匹配边两种。
– 对于匹配边：由于性质3，如果都被标记，那么左部点一定被选，如果都没被标记，则右部点一定被选，一共m个匹配，则最多有m个点被选。
– 对于非匹配边，分三种情况：
– 左边非匹配点——右边匹配点，由构造方式可知，右边的匹配点一定被标记，所以右边被选中。
– 左边匹配点——右边非匹配点，假设左部匹配点被标记那么右边非匹配点一定也被标记，与性质2矛盾，所有左部点一定未被标记，那么左部点一定被选到了。
– 左边未匹配——右边未匹配：不存在，与最大匹配矛盾

综上可知，此构造法选出的是一个覆盖且覆盖的点数最多m个，即最小点覆盖<=最大匹配数。

由于最小点覆盖>=最大匹配数&&最小点覆盖<=最大匹配数，故最小点覆盖最大匹配数

2. 最大独立集

• 最大独立集：选取尽可能多的点使得点集中所有点两两之间无边相连。
• 最大团：选取尽可能多的点使得点集中所有点两两之间都有边相连，与最大独立集互补。
• 定理：最大独立集 = n – 最大匹配数（n为图的节点个数）
• 证明：我们要选择尽可能多的点使得两两之间无边相连，反向考虑就是找最少的点使得拆散所有的边，那么我们只要找到最小点覆盖，然后把最小点覆盖里的点全都去掉，那么图中就不存在边了，那么剩下的就是最大独立集，由于最小点覆盖数=最大匹配数，故最大独立集 = n – 最大匹配数

3. 最小路径点覆盖

• 定义：在一个有向无环图中（DAG）用最少的不相交的简单路径覆盖所有的点。
  
  

如上图（左）的最小路径覆盖为：1->2->5, 3, 4（因为不能相交，所有路径数为3），我们很轻松的可以发现一个性质：每条路径的出度和入度都不超过1（因为不能相交）
– 定理：拆点构造二分图：将DAG中每个点x拆成x和x+n两个点，分别作为一张新二分图的左部和右部，则 编号为1 – n的点为二分图左部，n+1 – 2n的点为右部，对于原图每条有向边（x，y）， 在二分图的左部点x与右部点y+n之间连边，得到拆点二分图，记为G’（上图右），则最小路径覆 盖=原图点个数-G’的最大匹配数。
– 证明：由于每条路径的出度和入度都不超过1，所以每条路径对应二分图中的一个匹配（我们可以把二分图的左部看成出点，右部看成入点，每条原图的有向边都是从左部出点连向右部入点的，由于路径的性质，每个路径的出点和入点一 一对应，满足二分图匹配的性质），并且每条路径的终点必然对应一个左部的非匹配点。那么我们要让路径数最少，就是要让左部非匹配点最少，就是让二分图的匹配最多，所以最少路径数就等于原图点数减去二分图的最大匹配数。
– 最小路径可重复点覆盖：在一个有向无环图中（DAG）用最少的可相交的简单路径覆盖所有的点。
– 方法：先对DAG求一次传递闭包，然后当作求最小路径点覆盖。
– 原理：若两条路径相交，你们说明有两点a，b通过相交点连通，那么可以直接把ab 连接起来，跳过相交点，对所有的点都这样操作，然后要求路径不可相交，那么就 是最小路径点覆盖问题。
– floyd求传递闭包模板：

void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (mp[i][k] && mp[k][j]) mp[i][j] = 1;
}

六、典型例题及建图

1.Strategic Game HDU-1054（最小点覆盖）

• 题意：给一个具有 n 个点的树的所有边的信息，现在问最少需要多少个点放到树上，使得树的任意一条边都至少有一个端点被覆盖
• 思路：实质是要求最小点覆盖数，由于树是天然二分图（树没有回路），因此可以倍点法建图， 求树的最大匹配最后除以 2 即可。
• 要点：掌握倍点法建图技巧，就是将一张图的所有点作为左部，复制所有的点作为右部构建一个二分图，两边也根据原题连两条边，所以最后求出来的最大匹配也是实际最大匹配的两倍。注意这个技巧是在你已经判断题目给你的图是一个二分图模型的时候才能使用（比如本题树是个二分图已知），否则你应该用染色法判断二分图顺便在染色过程中建图（相同颜色为左部或者右部）。
• 代码：

#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define LL longlong
using namespace std;
const int maxn = 1e4 + 10;
bool vis[maxn];
int link[maxn];
vector<int> mp[maxn];

bool dfs(int x) {
    for (int i = 0; i < mp[x].size(); ++i) {
        int y = mp[x][i];
        if (!vis[y]) {
            vis[y] = true;
            if (link[y] == -1 || dfs(link[y])) {
                link[y] = x;
                return true;
            }
        }
    }
    return false;
}

int hug(int n) {
    int ans = 0;
    for (int i = 0; i < n; ++i) {
        memset(vis, false, sizeof(vis));
        if (dfs(i)) ans++;
    }
    return ans;
}
int main(int argc, char const *argv[]) {
    int n;
    while (~scanf("%d", &n) && n) {
        memset(link, -1, sizeof(link));
        for (int i = 0; i < n; ++i) {
            mp[i].clear();
        }
        for (int i = 0; i < n; ++i) {
            int x, y, t;
            scanf("%d:(%d)", &x, &t);
            while (t--) {
                scanf("%d", &y);
                mp[x].push_back(y);
                mp[y].push_back(x);
            }
        }
        printf("%d\n", hug(n) / 2);
    }
    return 0;
}

2.Air Raid HDU – 1151（最小路径点覆盖）

• 题意：一个城镇，所有街道都是单行的且不成环，每个街道与两个路口相连。 求最小数量的伞兵降落在一个路口，使他们可以通过街道访问所有的路口，同 一个路口不能经过多个伞兵。
• 思路： 城镇看成DAG图，街道为边，路口为点。 用最少的伞兵，去访问所有的点，即用最少的路径覆盖所有的点，最小路径覆盖问题。
• 代码：

#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define LL longlong
using namespace std;
const int maxn = 1e4 + 10;
bool vis[maxn];
int link[maxn];
vector<int> mp[maxn];

bool dfs(int x) {
    for (int i = 0; i < mp[x].size(); ++i) {
        int y = mp[x][i];
        if (!vis[y]) {
            vis[y] = true;
            if (link[y] == -1 || dfs(link[y])) {
                link[y] = x;
                return true;
            }
        }
    }
    return false;
}

int hug(int n) {
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        memset(vis, false, sizeof(vis));
        if (dfs(i)) ans++;
    }
    return ans;
}
int main(int argc, char const *argv[]) {
    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n >> m;
        memset(link, -1, sizeof(link));
        for (int i = 0; i <= n; ++i) {
            mp[i].clear();
        }
        for (int i = 0; i < m; ++i) {
            int x, y;
            scanf("%d %d", &x, &y);
            mp[x].push_back(y);
        }
        printf("%d\n", n - hug(n));
    }
    return 0;
}

3.奔小康赚大钱 HDU – 2255 （KM模板题）

• 中文题不给题意，思路：将村民当为左部点，村庄当右部点建带权二分图，求最大权匹配即可
• 代码：

#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define LL longlong
using namespace std;
const int MAXN = 310;
const int INF = 0x3f3f3f3f;
int nx,ny;//两边的点数
int g[MAXN][MAXN];//二分图描述
int linker[MAXN],lx[MAXN],ly[MAXN];//y中各点匹配状态，x,y中的点标号
int slack[MAXN];
bool visx[MAXN],visy[MAXN];

bool DFS(int x)
{
    visx[x] = true;
    for(int y = 0; y < ny; y++)
    {
        if(visy[y])continue;
        int tmp = lx[x] + ly[y] - g[x][y];
        if(tmp == 0)
        {
            visy[y] = true;
            if(linker[y] == -1 || DFS(linker[y]))
            {
                linker[y] = x;
                return true;
            }
        }
        else if(slack[y] > tmp)
            slack[y] = tmp;
    }
    return false;
}
int KM()
{
    memset(linker,-1,sizeof(linker));
    memset(ly,0,sizeof(ly));
    for(int i = 0;i < nx;i++)
    {
        lx[i] = -INF;
        for(int j = 0;j < ny;j++)
            if(g[i][j] > lx[i])
                lx[i] = g[i][j];
    }
    for(int x = 0;x < nx;x++)
    {
        for(int i = 0;i < ny;i++)
            slack[i] = INF;
        while(true)
        {
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));
            if(DFS(x))break;
            int d = INF;
            for(int i = 0;i < ny;i++)
                if(!visy[i] && d > slack[i])
                    d = slack[i];
            for(int i = 0;i < nx;i++)
                if(visx[i])
                    lx[i] -= d;
            for(int i = 0;i < ny;i++)
            {
                if(visy[i])ly[i] += d;
                else slack[i] -= d;
            }
        }
    }
    int res = 0;
    for(int i = 0;i < ny;i++)
        if(linker[i] != -1)
            res += g[linker[i]][i];
    return res;
}
int main()
{
    int n;
    while(scanf("%d",&n) == 1)
    {
        for(int i = 0;i < n;i++)
            for(int j = 0;j < n;j++)
                scanf("%d",&g[i][j]);
        nx = ny = n;
        printf("%d\n",KM());
    }
    return 0;
}

4.Tour HDU – 3488 (KM算法变形)

• 题意：有N个城市,M条街道,每条街道是单向的,现在要你设计多条路线覆盖所有的点,每条路线都是一个环,并且每个点仅能被一条路线覆盖且只经过一次(终始点除外)。
• 思路：因为每个顶点只出现一次，那么每个顶点只关联两个顶点入度顶点和出度顶点，所以构造二分图，将一个点u拆成u,u’。那么对于这个二分图如果存在着完美匹配的话，那么原图中一定存在若干个环，环中包含每个顶点，对于权值之和最小，只需求最小权匹配即可，最小权匹配求法很简单，只要在建图时把边权值取反，那么原来最大的边权值就最小了，然后跑一遍KM算法，最终答案再取反一次即可。
• 代码：

include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;

int N, M;

const int INF = 0x3f3f3f3f;
int w[205][205];
int lx[205], ly[205];
int sx[205], sy[205];
int match[205], slack[205];

int path(int u) {
    sx[u] = 1;
    for (int i = 1; i <= N; ++i) {
        if (sy[i]) continue;
        int t = lx[u] + ly[i] - w[u][i];
        if (!t) {
            sy[i] = 1;
            if (!match[i] || path(match[i])) {
                match[i] = u;
                return true;
            }
        } else {
            slack[i] = min(slack[i], t);
        }
    }
    return false;
}

void KM() {
    memset(match, 0, sizeof (match));
    memset(lx, 0x80, sizeof (lx));
    memset(ly, 0, sizeof (ly));
    for (int i = 1; i <= N; ++i) {
        for (int j = 1; j <= N; ++j) { 
            lx[i] = max(lx[i], w[i][j]);
        }
    }
    for (int i = 1; i <= N; ++i) {
        memset(slack, 0x3f, sizeof (slack));
        while (1) {
            memset(sx, 0, sizeof (sx));
            memset(sy, 0, sizeof (sy));
            if (path(i)) break;
            int d = INF;
            for (int j = 1; j <= N; ++j) {
                if (!sy[j]) d = min(d, slack[j]);
            }
            for (int j = 1; j <= N; ++j) {
                if (sx[j]) lx[j] -= d;
                if (sy[j]) ly[j] += d;
                else slack[j] -= d;
            }
        }
    }
    int ret = 0;
    for (int i = 1; i <= N; ++i) {
        ret += w[match[i]][i];
    }
    printf("%d\n", -ret);
}

int main() {
    int T, x, y, ct;
    scanf("%d", &T);
    while (T--) {
        scanf("%d %d", &N, &M);
        memset(w, 0x80, sizeof (w));
        for (int i = 1; i <= M; ++i) {
            scanf("%d %d %d", &x, &y, &ct);
            w[x][y] = max(w[x][y], -ct);
        }
        KM();
    }
    return 0;    
}