一、前言

$KMP$ 算法可以说是我学过的算法里最让我印象深刻的一个算法了。初学 $KMP$ 的时候真的是抓耳挠腮，硬啃了一下午的博客才勉强可以自己独立推一遍算法的整个流程。第二次学习 $KMP$ 是为了在数据结构课上给同学们介绍这个算法，自己学和教会别人又是不一样的难度，于是我又重新学习了一遍，但这一次学习时有很多之前觉得很抽象的东西都突然茅塞顿开了，为了讲解的效果，我还反复推导了几次算法，确保讲课的流畅。第三次学习 $KMP$ 是为了给集训队的学弟们讲这个算法，而竞赛更偏重于算法的应用，所以我在重新推演了一次算法后又找了一些经典例题。自此，对于 $KMP$ 的理解可以说是挺明晰了。最近，我又学习了 AC自动机，很巧的是，AC自动机的思想和 $KMP$ 是一样的，于是我又“被迫”重温了一遍 $KMP$ ，既然那么有缘分，不如就写篇博客吧。

二、 KMP算法

KMP算法~~（又称看毛片算法）~~，名字取自它的三个共同发明者名字的首字母，是一个高效率的字符串匹配算法。主要解决这样一个问题：有一个 $S$ 串（称为匹配串）和一个 $P$ 串（称为模式串 $pattern$）,问在 $S$ 中是否出现过 $P$ 以及出现过几次的问题。

2.1 朴素算法

首先我们可以想到一个不计效率的暴力做法：将 $S$ 串的 $i$ 位置作为起点与 $P$ 串进行比较，如果整个字符串匹配了则退出，如果在某个位置失配了，则 $S$ 从 $i+1$ 开始作为起点与整个 $P$ 串重新比较，直到 $S$ 串的每个位置都与 $P$ 比较过后结束，假设 $S$ 串长度为 $n$，$P$ 串长度为 $m$ ，则整体的时间复杂度为 $O(nm)$，上述流程的代码如下：

int i = 0;
while (i < n) {
    int j = 0;
    while (j < m && s[i] == p[j]) {//相同则继续比较下一个字符
        i++, j++;
    }
    if (j >= m) break;//成功匹配
    i = i - j;//回到起点
    i++;//移动到起点下一个位置
}

2.2 KMP思想

上面整个暴力做法效率太低了，我们考虑如何进行优化？我们在模拟暴力的匹配过程中可以发下，每次失配后 $i$ 指针和 $j$ 指针都要回退很大的一段长度，然后重新比较，我们如果可以根据已有的信息通过理论分析来减少回退的距离那么就能提高匹配的效率了, $KMP$ 算法就是这样去考虑的。其实 $KMP$ 本质就是一个设计精妙的动态规划。

假设我们某次匹配失败了，如下图所示，绿色部分表示匹配成功的部分，在 “x” 处匹配失败。假如 $P$ 串的某个前缀子串和后缀子串相同（红色部分），那么我们就可以利用这个信息减少回退。

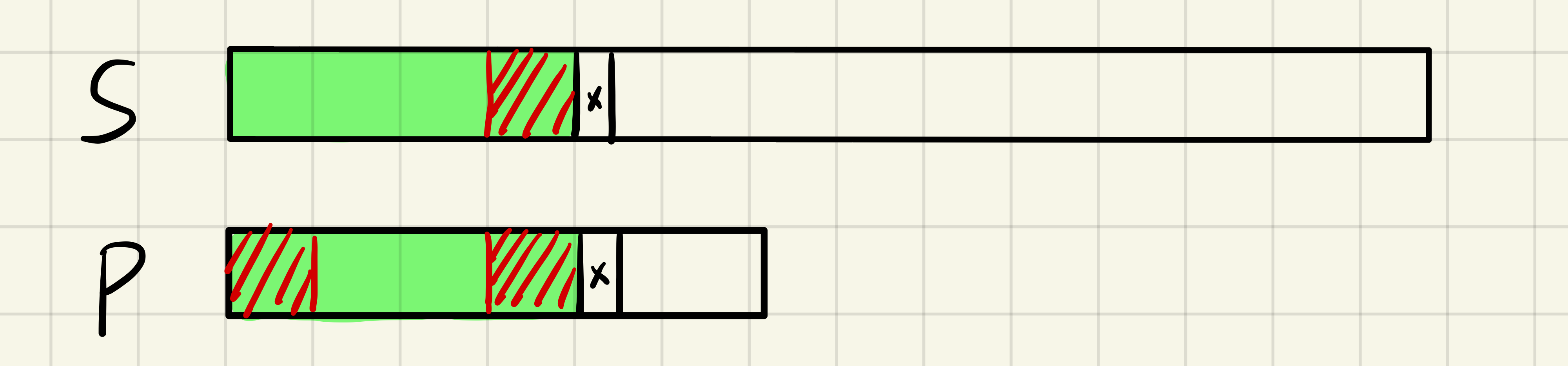
由于绿色部分是相同的，很容易可知，$S$ 串对应的红色部分也和 $P$ 串的两个红色部分相同，我们可以将 $S$ 不动，P串向后移动直到 $S$ 的红色部分和 $P$ 串的前半个红色对齐，然后继续比较下一个位置是否相同即可，如下图所示：

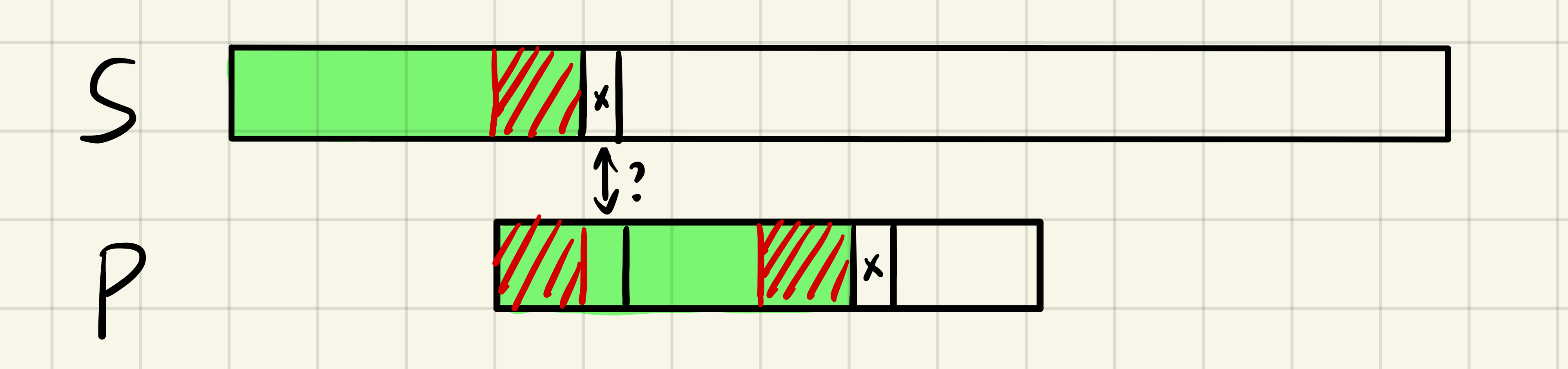
既然如此，那么我们如果可以找到 $P$ 串最长的红色部分，那么我们就可以让 $P$ 串移动的距离最少使得效率最大化。下面证明一下此结论的正确性：假设某次匹配失败后（图中绿色部分），P串向后移动了一段最短的距离，并成功匹配，如图中红色部分。由于红色部分一一对应相等，必然可得蓝色部分也相等，我们可以发现在 $S$ 串中，蓝色部分是绿色部分的后缀，在 $P$ 串中蓝色部分是绿色部分的前缀，那么要让 $P$ 串移动的距离最小，其实就是让蓝色部分尽量长，即让绿色部分的前缀和后缀相同且尽量长。

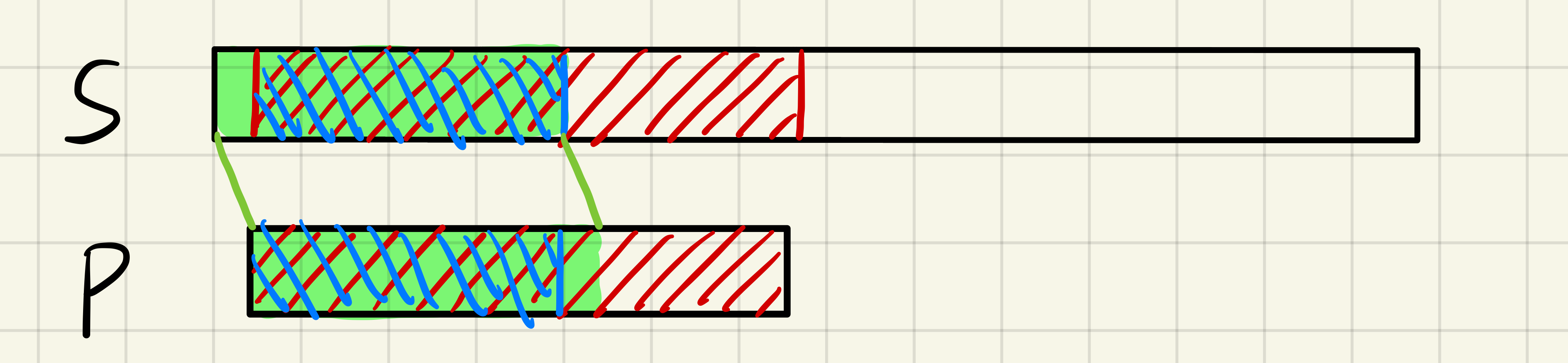
好了，现在我们已经找到优化匹配过程的方法了，就剩下一个问题：如何求得 $P$ 串的某个前缀子串的最长的相同的前缀和后缀的长度（有点拗口，多读几遍理解）呢？这就是 $KMP$ 的精妙之处，也是初学者最难理解的部分：$next$ 数组。

2.3 next数组求解

2.3.1 什么是next数组？

因为无法知道 $P$ 的那些子串需要用到最长的相同的前缀后缀长度，所以最稳妥的方法就是预处理出P串的每个前缀子串的最长的相同的前缀后缀长度。于是引出 $next$ 数组的定义：$next[i]$ 表示 $P$ 串下标为 **$0$ 到 $i-1$ **的子串 $x$ 的某个前缀与 $x$ 的后缀相同，记录最长的长度（注意记录的是0到 i-1 的子串！！），另外这里的前缀和后缀必须都是非平凡的（即不包括自身），比如abcd的前缀只有a，ab，abc，后缀只有d，cd，bcd，后面描述中的前缀后缀都是非平凡的，不再重复。

举个例子：

idx =  0 1 2 3 4 5 6//下标
p[] =  a b a d a b c//p串
n[] =  0 0 0 1 0 1 2//对应的next数组

//解释:
//next[3] = 1,因为0到2的串为aba，最长相等的前缀和后缀为“a”

2.3.2 怎么求next数组？

明确next数组的定义后，思考如何求解next数组。

如图，假设计算 $next[i+1]$ 时某个时候，发现 $p[i] neq p[j]$ ，我们就要考虑有没有更小的一个前缀可以和后缀匹配，假设子串 $p[0…j-1]$ 中存在一个最长的前缀和后缀相等（蓝色部分），那么由于绿色部分相等，我们可以推得，绿色中也有一部分和前缀的蓝色相同，那么我们只要比较$p[k]$ 和 $p[i]$ 是否相等，如果不相等继续找 $k$ 之前子串的最长相等前缀后缀，直到发现相等或者 $k$ 到边界0，这样就能求得 $next[i+1]$ 。

我们发现 $j$ 指针的转移依据是下标为0到j-1的子串的最长前缀后缀，即通过 $j = next[j]$ 不断向前移动 $j$ 指针，直到发生匹配记录相应的 $next$ 值，或者 $j = 0$ 时也失配则结束寻找相应的 $next = 0$，由于要用到之前的 $next$ 信息，所以我们可以用递推的方式从小往大求得所有的next值，注意边界 $next[0] = -1$ ，这是特殊规定的，但也有它的巧妙之处，先给出代码：

int i = 0, j = -1;
next[i] = j;
while(i < m) {
    if(p[i] == p[j] || j == -1) {
        i++,j++;
        next[i] = j;
    }else {
        j = next[j];
    }
}

代码可能有点地方不太容易理解，主要就是下标的变换，这也是我初学 $KMP$ 时最头疼的一个地方，下面对主要部分进行分析，但最好还是手动模拟逐一理解：

j = next[j]; ，这一句是用来指向下一个待比较的位置，由于next[j] 存的是0到j-1这个子串的最长前缀后缀长度，而我们的下标是从0开始的，所以将 j 变成 next[j] 刚好可以指向最长前缀的下一个位置（如长度为2，下标从0开始，如果指向2，那么实际指向的是第三个字母）。
if(p[i] == p[j] || j == -1) ，前半部分表示找到匹配，那么就可以修改对于的next值，后一般部分表示 $j$ 走到了边界，那么也可以修改对应的 next 值，所以放在一起判断，如果没到边界或者匹配失败可以通过将 $j$ 指针转移来继续寻找匹配。
i++,j++;next[i] = j，这一句话也是最巧妙的，注意一定要先执行自增操作，再进行赋值。再次强调 $next[i]$ 的含义：表示 0 到 i – 1之间的最长相同前缀后缀长度。
- 如果 $p[i] = = p[j]$ 那么需要更新的实际上是 $i+1$ 的next值，同时由于下标从0开始，所以实际长度为最后一个字母的下标+1，即 $j+1$ ，所以 $j$ 也要加1。
- 如果 $j = = -1$ ,那么说明没有字母可以和 $p[i]$ 匹配，那么 $$next[i+1] = 0$，则通过 i++,j++ 使得 $i$ 变成了 $i+1$ ，$j$ 变成了 0，符合实际要求。
- 当然，这里的 i++,j++ 不仅仅因为为了满足next的定义，还有使得 $i$ 指针和 $j$ 指针向下移动一格的目的（因为在这个条件分支中，要么完成匹配，需要进行下一个字符的匹配；要么走到边界没有可以匹配的了，进行下一轮的匹配）。所以这里的操作可以说是一举多得！

2.4 KMP代码实现

现在我们有 $next$ 数组了，那么我们再回头将 $KMP$ 代码化吧！如果忘记了怎么用 $next$ 优化匹配的话，可以往前翻重新回顾一下。下面直接给出 $KMP$ 的核心代码：

//S为匹配串，P为模式串，n表示S串长度，m表示P串长度
//i为S的指针，j为P的指针
int i = 0, j = 0;
while(i < n && j < m) {
    if(j == -1 || s[i] == p[j]) {
        i ++,j++;
    }else {
        j = next[j];
    }
}
if(j == m) puts("YES");//找到匹配
else puts("NO");//未找到

我们可以发现， $KMP$ 的写法几乎和 $next$ 的求解一模一样，这里就不做过多分析，讲解一下大致流程：首先 $i$ 和 $j$ 都指向起点 0 ,进入循环，如果两者匹配，则同时+1，继续匹配下一个字符，如果发现失配，那么就将 $j$ 指向 $next[j]$ ，同时由于下标从0开始，所以指向的也正好是下一个待匹配的位置，继续匹配，如果一直失配则会遇到边界 $next[0] = -1$ ，则将$i+1,j+1$ ，即$i$进入下一个位置和 $j = 0$ 比较。循环的边界是 $i$ 或 $j$ 走到字符串外面，如果 $j$ 走到字符串外面了，说明 $S$ 串中存在匹配。

2.5 KMP时间复杂度分析及优化

分析代码，我们可以发现匹配的过程中 $i$ 是不会往回退的，$j$ 虽然会回退，但也是有限的几次可以忽略，所以这里的复杂度为 $O(n)$，另外还有求 $next$ 数组，同理可得复杂度为 $O(m)$，故总体复杂度为 $O(n+m)$。

KMP将一个乘法级别的复杂度降低到了加法级别，可以说是巨大的提升，那么是否还有可以优化的地方呢？

观察下面这个情况：

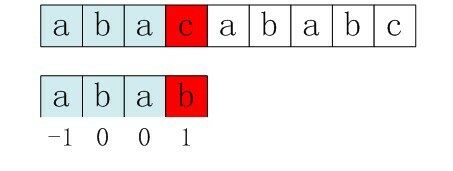
我们发现 $s[3] neq p[3]$ ，则令 $j = next[3] = 1$ ，即比较 $s[3]$ 和 $p[1]$ 这必然是失配的，因为一开始 $s[3] neq p[3] = ‘b’$，而

$p[1]$ 也等于‘b’，所以必然失配，对于这种可以推得的“必然失配”的情况，我们都可以将其优化掉。考虑什么时候会出现这的情况：只有当$p[j] = p[next[j]]$ 时才会出现上述的情况，那么当 $p[j] = p[next[j]]$ 是，我们只要让 $next[j] = next[next[j]]$ 就行了，这部分的优化可以在 $next$ 数组的求解中完成，优化后的代码如下：

int i = 0, j = -1;
next[i] = j;
while(i < m) {
    if(p[i] == p[j] || j == -1) {
        i++,j++;
        if(p[i]!=p[j])
            next[i] = j;
        else next[i] = next[j];
    }else {
        j = next[j];
    }
}

三、AC自动机

3.1 简介

AC自动机顾名思义就是~~自动AC的机器，可以帮助你将难题直接Accept掉~~，有些东西还真不能顾名思义，AC自动机全称为Aho-Corasick automaton，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。所谓多模匹配算法，最常见的例子是给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。要学习AC自动机，首先需要先学会 Trie（字典树），没了解过的可以先去了解一下，很简单的一种数据结构，下文都建立在掌握字典树的基础上展开。AC自动机算法和KMP很像，一共分为三步：构造一棵 Trie 树，构造失败指针和模式匹配过程。

3.2 失败指针

假设现在有四个单词：ash、 shex 、bcd 、sha ，我们可得下面这样的一颗 Trie树：

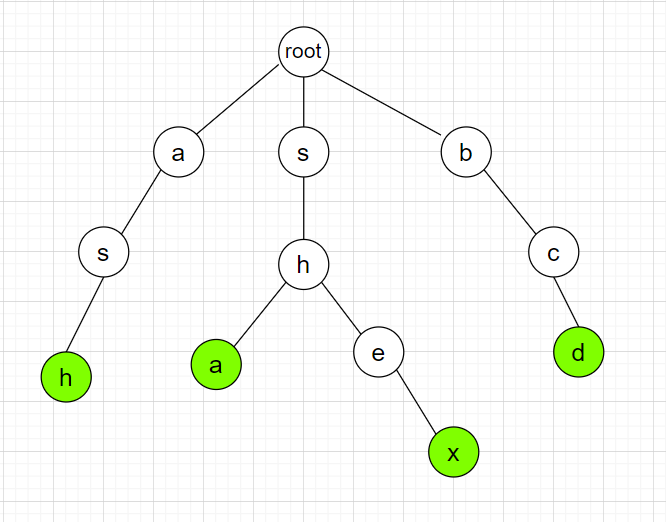
我们定义一个 $fail$ 指针：对于某个节点 $p$ ，它的 $fail$ 指针指向某个节点 $q$ ，我们令：

以根节点为起点到 $p$ 的简单路径（即最短的那条路）上经过的所有字符构成的字符串为 $S$ 。
以根节点为起点到 $q$ 的简单路径上经过的点构成的字符串为 $P$ 。

$q$ 节点满足，$S$ 的最长的非平凡后缀（即不包括自身的后缀）与 $P$ 串相等，如果不存在这样一个点 $q$ ，则 $fail$ 指向根节点，据此我们可以画出上图的字典树中每个节点的 $fail$ 指针：

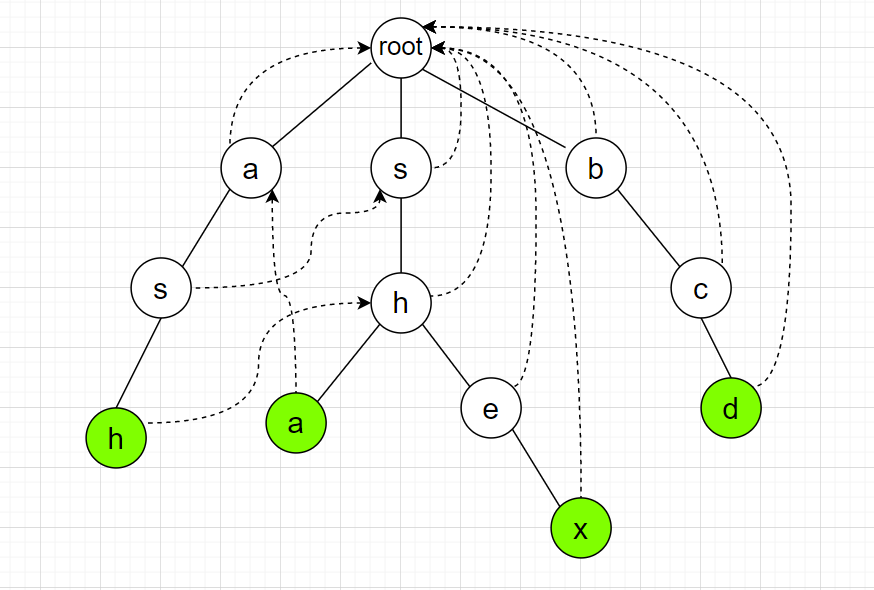
上面是 $fail$ 指针的抽象定义，其主要功能就是在匹配串匹配失败后，将指针转移到 $fail$ 指针指向的地方,这样就不用回溯,而可以一路匹配下去了。其实 $fail$ 指针指向的就是当前搜索的串的后缀可以匹配的所有以根节点为起点的子串的前缀的最大值，假设我们有一个匹配串 $S$ 在匹配的过程中的某个位置发生失配了，那么以失配位置为结尾的这段字符串的一部分有可能成为某个单词（匹配串）的前缀，所以我们跳到最大的前缀继续比较。

3.3 模式匹配

了解了 $fail$ 指针的定义，我们进行文本串的匹配，假设有个匹配串 ashex，我们沿着字段树向下搜索（蓝色箭头为路径）：

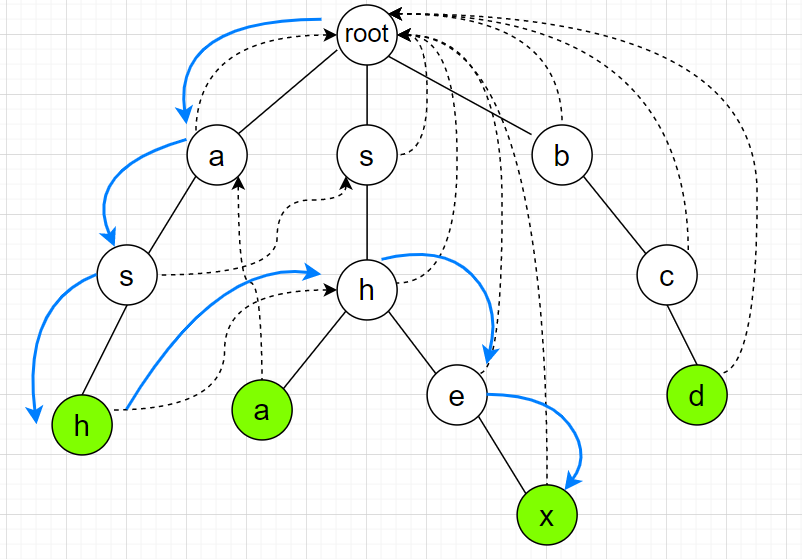
一直沿着字典树向下走，直到发现走到一个绿色节点，说明找到了某个单词（字典树中如果某个节点为某个单词的最后一个字符，则会标记这个节点，图中以绿色为标记），此时 ‘h’ 没有后续节点，匹配失败，我们通过最左边的这个 ‘h’ 的 $fail$ 指针，转移到了中间的这个 ‘h’ ，然后继续向下走，走到 ‘x’ 后又发现绿色节点，则又找到一个单词。此时’x’没有后续节点，匹配失败，则通过 $fail$ 指针转移，走到 root 节点，匹配结束,整个过程发现两个单词。

3.4 代码模板

以 AcWing 1282. 搜索关键词为例，给出模板：

由于这道题收录在付费课程中，可能无法查看题目，这里直接给出题目（强推Acwing的算法系列课程，真的很棒！）：

1282.搜索关键词

给定 $n$ 个长度不超过 $50$ 的由小写英文字母组成的单词，以及一篇长为 $m$ 的文章。

请问，有多少个单词在文章中出现了。

输入格式

第一行包含整数 $T$，表示共有 $T$ 组测试数据。

对于每组数据，第一行一个整数 $n$，接下去 $n$ 行表示 $n$ 个单词，最后一行输入一个字符串，表示文章。

输出格式

对于每组数据，输出一个占一行的整数，表示有多少个单词在文章中出现。

数据范围

$1≤n≤10^4,$

$1≤m≤10^6$

输入样例：

1
5
she
he
say
shr
her
yasherhs

输出样例：

代码

可以类比 KMP 其实也是用递推的思想，即使用上面几层的节点求下面的 $fail$ 指针，由于按层求，所以用bfs遍历，具体看代码吧，解释起来有点麻烦，~~代码详解先鸽着，有空的话再补充。~~

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e4 * 55 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL; 
int tr[maxn][26],idx; //字典树
int cnt[maxn];//记录该单词出现次数
int ne[maxn];//失败时的回溯指针
char s[maxn * 10];

void insert() {//建立Trie树
    int p = 0;
    for (int i = 0; s[i]; i++) {
        int t = s[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++idx;
        p = tr[p][t];
    }
    cnt[p]++;//当前节点单词数+1
}

void get_next() {
    queue<int> q;
    for (int i = 0; i < 26; i++) {//将第二层所有出现了的字母扔进队列
        if (tr[0][i]) q.push(tr[0][i]);
    }
    //ne[now]    ->当前节点now的失败指针指向的地方
    //tr[now][i] -> 下一个字母为i+'a'的节点的下标为tire[now][i]
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {//查询26个字母
            int v = tr[u][i];
            if (!v) continue;
            //如果有这个子节点为字母i+'a',则让这个节点的失败指针
            //指向他父亲节点的失败指针所指向的那个节点的下一个节点
            int j = ne[u];
            while (j && !tr[j][i]) j = ne[j];
            if (tr[j][i]) j = tr[j][i];
            ne[v] = j;
            q.push(v);
        }
    }
}

int main(int argc, char const *argv[]) {
    int t;
    cin >> t;
    while (t--) {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;
        int n;
        cin >> n;
        for (int i = 0; i < n; i++) {
            scanf("%s", s);
            insert();
        }
        get_next();
        scanf("%s", s);
        int res = 0;
        for (int i = 0, j = 0; s[i]; i++) {//遍历文本串
            int t = s[i] - 'a';
            while (j && !tr[j][t]) j = ne[j];
            j = tr[j][t];
            int p = j;
            while (p) {
                res += cnt[p];
                cnt[p] = 0;
                p = ne[p];
            }
        }
        printf("%dn", res);
    }
    return 0;
}

AC自动机优化

和 $KMP$ 一样，$fail$ 指针也有相应的优化，在计算 $fail$ 指针时这样进行：

void get_ne() {
    for (int i = 0; i < 26; i++) {
        if (tr[0][i]) q.push({tr[0][i]});
    }
    while (q.size()) {
        int now = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {
            int p = tr[now][i];
            if (!p)
                tr[now][i] = tr[ne[now]][i];
            else {
                ne[p] = tr[ne[now]][i];
                q.push(p);
            }
        }
    }
}

~~继续鸽，有空再解释~~

四、参考文献

从头到尾彻底理解KMP（2014年8月22日版）（v_JULY_v大佬的超详细博客，第一次接触kmp就啃的他的博客）

Acwing KMP代码（y老师的模板，十分简短）

AC自动机百度百科

AC自动机算法详解(图解)及模板