莫队学习总结
|
2,940
|
2
|
ACM生涯,算法学习总结

6355 字
|
47 分钟

一、基础莫队

例题

Acwing 2492.HH的项链

HH 有一串由各种漂亮的贝壳组成的项链。

HH 相信不同的贝壳会带来好运，所以每次散步完后，他都会随意取出一段贝壳，思考它们所表达的含义。

HH 不断地收集新的贝壳，因此他的项链变得越来越长。

有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同的贝壳？

这个问题很难回答，因为项链实在是太长了。

于是，他只好求助睿智的你，来解决这个问题。

输入格式

第一行：一个整数 $N$，表示项链的长度。

第二行：$N$ 个整数，表示依次表示项链中贝壳的编号（编号为 $0$ 到 $1000000$ 之间的整数）。

第三行：一个整数 $M$，表示 $H$ 询问的个数。

接下来 $M$ 行：每行两个整数，$L$ 和 $R$，表示询问的区间。

输出格式

$M$ 行，每行一个整数，依次表示询问对应的答案。

数据范围

$1≤N≤50000$
$1≤M≤2×10^5$
$1≤L≤R≤N$

输入样例：

6
1 2 3 4 3 5
3
1 2
3 5
2 6

输出样例：

2
2
4

1.1 暴力做法

我们先来思考最暴力的方法：对于每次询问，遍历一遍区间内的所有数字，用一个桶记录数字出现的次数，出现次数 $\ge 1$ 的个数就是答案，维护一个 $ans$ 变量记录答案，每当有新的数字从0个变成1个时，将 $ans+1$ ，这样就不用遍历整个桶统计有几个数字 $\ge 1$ ，由于单次遍历是 $O(n)$ 的，所以总复杂度为 $O(nm)$。

1.2 莫队思想

介绍莫队之前，先介绍本题的另外一种做法：

类似双指针的方式，设当前要统计的区间为 $L$ 到 $R$ ,设置两个指针记录上一次统计的区间为 $X$ 到 $Y$ ,那么只要控制指针，将 $X$ 向 $L$ ，$Y$ 向 $R$ 靠齐即可，在移动的过程中可能会在区间中加数或减数，同时更新桶中对应数字的个数，当某个数字个数从0变为1则$ans+1$,从1变为0则 $ans-1$ ，由于相邻的两次查询最坏可能使得指针移动 $n$ 次，所以这种做法的时间复杂度也是 $O(nm)$的。

莫队的基本做法也是利用双指针，但是利用了分块的思想对查询的次序进行了优化，使得整体复杂度在 $O(n\sqrt n)$ 级别。

我们先来思考，如何优化可以使得上面的双指针变快，只要减少指针的回走就能降低时间。所以最理想的情况就是使得所有查询的左右区间分别是单调递增的，那么双指针就不会回退，整体复杂度变成了 $O(n)$ ，但是这是不可能的，比如下面的这个例子：左区间单调递增，但是右区间不满足。

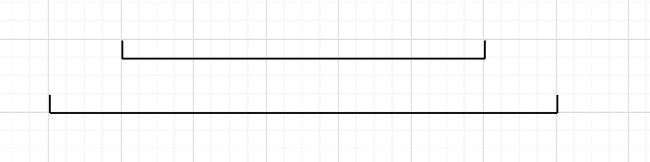
image-20210803085635517

再引入分块的思想，就是莫队的完整思想了：先将所有查询区间按照左端点分成 $\sqrt n$ 块，每块的长度也是 $\sqrt n$ ，然后在每块内按照右端点递增排序，这样就能保证每块的右端点是单调递增的了。

分析复杂度：

  • 对于右端点，由于每块内右端点是单调递增的，所以每块最坏移动 $n$ 次，一共 $\sqrt n$ 个块，整体 $n\sqrt n$ 的复杂度。

  • 对于左端点，分为块内移动和块间移动：

    • 块内：最坏块内每次询问都要移动 $\sqrt n$ 次（区间长度次），最坏可能一个块内就有 $m$ 次询问，整体复杂度为 $m\sqrt n$
    • 块间：最坏每次块间移动距离为 $2\sqrt n$ ，一共 $\sqrt n$ 个块，最多跨越 $\sqrt n -1$ 次，整体复杂度为 $2n$

综上，取最大值，复杂度为 $m\sqrt n$。

1.3 基础莫队代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int a[maxn];
int len;
int get(int i) { return i / len; }//得到左区间对应的块的编号
struct node {
    int l, r, i;
    bool operator<(const node &t) const {//双关键字排序
        int a = get(l), b = get(t.l);
        if (a != b) return a < b;
        return r < t.r;
    }
} q[maxn << 1];
int tong[maxn * 10];
int ans[maxn << 1];
void add(int x, int &cnt) {//加数操作
    if (tong[x] == 0) cnt++;
    tong[x]++;
}
void del(int x, int &cnt) {//删数操作
    tong[x]--;
    if (!tong[x]) cnt--;
}
int main(int argc, char const *argv[]) {
    int n;
    cin >> n;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) scanf("%d", a + i);
    int m;
    cin >> m;
    for (int i = 1; i <= m; i++) {//记录区间
        scanf("%d %d", &q[i].l, &q[i].r);
        q[i].i = i;
    }
    sort(q + 1, q + 1 + m);
    int l = 1, r = 0, cnt = 0;//左右指针和答案变量
    for (int i = 1; i <= m; i++) {
        while (l < q[i].l) del(a[l++], cnt);
        while (l > q[i].l) add(a[--l], cnt);
        while (r < q[i].r) add(a[++r], cnt);
        while (r > q[i].r) del(a[r--], cnt);
        ans[q[i].i] = cnt;//将答案记录到对应顺序的询问中
    }
    for (int i = 1; i <= m; i++) printf("%d\n", ans[i]);
    return 0;
}

二、带修改的莫队

例题

AcWing 2521. 数颜色

墨购买了一套 $N$ 支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。

墨墨会像你发布如下指令：

  1. Q L R 代表询问你从第 LL 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。
  2. R P Col 把第 $P$ 支画笔替换为颜色 $Col$。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入格式

第 1 行两个整数 $N,M$，​分别代表初始画笔的数量以及墨墨会做的事情的个数。

第 2 行 $N$ 个整数，分别代表初始画笔排中第 $i$ 支画笔的颜色。

第 3 行到第 $2+M$ 行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式

对于每一个 Query 的询问，你需要在对应的行中给出一个数字，代表第 $L$ 支画笔到第 $R$ 支画笔中共有几种不同颜色的画笔。

数据范围

$1≤N,M≤1000$
修改操作不多于 $1000$ 次，
所有的输入数据中出现的所有整数均大于等于 $1$ 且不超过 $10^6$。

输入样例：

6 5
1 2 3 4 5 5
Q 1 4
Q 2 6
R 1 2
Q 1 4
Q 2 6

输出样例：

4
4
3
4

2.1 思想

在基础莫队的基础上由于有修改操作，所以需要再增加一维代表时间，先按照左边界分块然后按照右边界分块然后按照时间升序排序。这里的时间的意识是当前查询位于哪次修改之后。初始没修改过的几次查询时间为0，第一次查询后的时间设为1，以此类推。对于修改操作可以看成一次删除和一次加数的操作，将需要被替换的数删去，然后将新的数加上。在指针移动的过程中，我们先将指针和待查询区间的左右边界匹配，然后再将当前时间和查询区间所在的区间匹配。在代码实现时有个小技巧：假设第 $t$ 次更新操作，将 $a[pos]$ 更新为 $col$ ，那么我们可以在更新完后 swap(a[pos],c[t].col)，即将第 $t$ 次修改的值与原数组中对应位置的值交换，这样下次如果需要撤销修改，可以直接再执行一次修改就行了（同样再进行一次swap），具体看代码。

2.2 带修改的莫队代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e4 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int len, n, m, mq, mc;
int get(int x) { return x / len; }
struct node {
    int id, l, r, ti;
    bool operator<(const node &tt) const {
        int a = get(l), b = get(tt.l);
        if (a != b) return a < b;
        a = get(r), b = get(tt.r);
        if (a != b) return a < b;
        return ti < tt.ti;
    }
} q[maxn];
PII c[maxn];
int a[maxn], tong[maxn * 100], ans[maxn];
void add(int x, int &res) {
    if (!tong[x]) res++;
    tong[x]++;
}
void del(int x, int &res) {
    tong[x]--;
    if (!tong[x]) res--;
}
int main(int argc, char const *argv[]) {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) scanf("%d", a + i);
    for (int i = 0; i < m; i++) {
        char op[2];
        int x, y;
        scanf("%s %d %d", op, &x, &y);
        if (op[0] == 'Q') {
            q[++mq] = {mq, x, y, mc};
        } else {
            c[++mc] = {x, y};
        }
    }
    len = sqrt(n) + 1;
    sort(q + 1, q + 1 + mq);
    int L = 1, R = 0, res = 0, now = 0;
    for (int i = 1; i <= m; i++) {
        int l = q[i].l, r = q[i].r, id = q[i].id, t = q[i].ti;
        while (L < l) del(a[L++], res);//将 L R 和 l r 对齐
        while (L > l) add(a[--L], res);
        while (R < r) add(a[++R], res);
        while (R > r) del(a[R--], res);
        //将 now 与 t 对齐
        while (now < t) {
            now++;
            int pos = c[now].first, col = c[now].second;
            if (pos >= l && pos <= r) {
                del(a[pos], res);
                add(c[now].second, res);
            }
            swap(a[pos], c[now].second);//交换，一定要交换两个数组中的值！
        }
        while (now > t) {
            int pos = c[now].first;
            if (pos >= l && pos <= r) {
                del(a[pos], res);
                add(c[now].second, res);
            }
            swap(a[pos], c[now].second);//交换
            now--;
        }
        ans[id] = res;
    }
    for (int i = 1; i <= mq; i++) printf("%d\n", ans[i]);
    return 0;
}

三、带回滚的莫队

例题

ACwing 2523. 历史研究

IOI 国历史研究的第一人——JOI 教授，最近获得了一份被认为是古代 IOI 国的住民写下的日记。

JOI 教授为了通过这份日记来研究古代 IOI 国的生活，开始着手调查日记中记载的事件。

日记中记录了连续 $N$ 天发生的时间，大约每天发生一件。

事件有种类之分。第 $i$ 天 $(1≤i≤N)$ 发生的事件的种类用一个整数 $X_i$ 表示，$X_i$ 越大，事件的规模就越大。

JOI 教授决定用如下的方法分析这些日记：

  1. 选择日记中连续的一些天作为分析的时间段
  2. 事件种类 $t$ 的重要度为 $t×$ (这段时间内重要度为 $t$ 的事件数)
  3. 计算出所有事件种类的重要度，输出其中的最大值

现在你被要求制作一个帮助教授分析的程序，每次给出分析的区间，你需要输出重要度的最大值。

输入格式

第一行两个空格分隔的整数 $N$ 和 $Q$，表示日记一共记录了 $N$ 天，询问有 $Q$ 次。

接下来一行 $N$ 个空格分隔的整数 $X_1…X_N$，$X_i$ 表示第 $i$ 天发生的事件的种类。

接下来 $Q$ 行，第 $i$ 行 $(1≤i≤Q)$ 有两个空格分隔整数 $A_i$ 和 $B_i$，表示第 ii 次询问的区间为 $[A_i,B_i]$。

输出格式

输出 $Q$ 行，第 $i$ 行 $(1≤i≤Q)$ 一个整数，表示第 $i$ 次询问的最大重要度。

数据范围

$1≤N≤10^5$,
$1≤Q≤10^5$,
$1≤X_i≤10^9$

输入样例：

5 5
9 8 7 8 9
1 2
3 4
4 4
1 4
2 4

输出样例：

9
8
8
16
16

2.1 题目分析

此题询问的不是一段区间内数字的个数，而是一段区间内所有数字和其个数乘积的最大值。对于最值，如果是向区间内增加一个数很好处理，只要将新加的数与当前最大值比较取较大值即可，那么如果区间内减去一个数，很难在 $O(1)$ 的时间内维护最值（虽然可以用一个堆维护，但是我们这里不讲堆的做法）。那么就要在基本莫队的基础上进行优化。另外，此题的数字取值很大但是个数在 $10^5$ 以内，所以需要进行一下离散化，具体在代码中体现。下面讲解带回滚的莫队的核心思想：

2.2 带回滚的莫队思想

由于分块后，每一块是相对独立的，所以我们只考虑查询的左端点都在某一个块时，此时有两种情况：右端点在块内，右端点在块外。

  • 对于右端点在块内的点，我们直接暴力处理，即遍历查询的整个区间维护最大值，这里的时间复杂度为 $m\sqrt n$。
  • 对于右端点在块外的点，我们将区间分成两部分：在块内的一部分和在块外的一部分，我们设 $L\ R$ 分别为两个指针，$l\ r$ 分别为询问的左右区间：
    • 对于在块内的一部分我们每次暴力遍历处理，初始 $L$ 指向当前块的右边界，然后将指针向右移动将所有的数加入直到碰到 $l$。在本次查询结束后，将指针 $L$ 重新移动回当前块的右边界。
    • 对于块外的一部分，由于分块中所有查询的右端点是递增的，所以每次查询只有加数的操作，不存在删数的操作，所以每次查询无需回滚，保持全过程即可。

具体结合代码就很好理解了！

2.3 代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
LL ans[maxn];

int a[maxn], cnt[maxn], n, m, len;
vector<int> num;
void add(int x, LL &res) {
    cnt[x]++;
    res = max(res, (LL)cnt[x] * num[x]);
}
int get(int x) { return x / len; }
struct node {
    int l, r, id;
    bool operator<(const node &t) const {
        int a = get(l), b = get(t.l);
        if (a != b)
            return a < b;
        else
            return r < t.r;
    }
} q[maxn];
int main(int argc, char const *argv[]) {
    cin >> n >> m;
    len = sqrt(n);
    for (int i = 1; i <= n; i++) scanf("%d", a + i), num.push_back(a[i]);
    sort(num.begin(), num.end());
    num.erase(unique(num.begin(), num.end()), num.end());//离散化
    for (int i = 1; i <= n; i++)
        a[i] = lower_bound(num.begin(), num.end(), a[i]) - num.begin();//a中记录离散化后的下标
    for (int i = 1; i <= m; i++) {
        scanf("%d %d", &q[i].l, &q[i].r);
        q[i].id = i;
    }
    sort(q+1,q+1+m);
    for (int i = 1; i <= m;) {
        int limit = get(q[i].l) * len + len - 1;//找到当前块的最右边界
        int j = i;
        while (j <= m && get(q[i].l) == get(q[j].l)) j++;//找到所有右边界在块内的询问
        //对于左右边界均处于块内的询问直接暴力处理
        while (i < j && q[i].r <= limit) {
            LL res = 0;
            int l = q[i].l, r = q[i].r, id = q[i].id;
            for (int k = l; k <= r; k++) add(a[k], res);
            ans[id] = res;
            for (int k = l; k <= r; k++) cnt[a[k]]--;
            i++;
        }
        //右端点在块外的需要双指针处理
        int L = limit + 1, R = limit;
        LL res = 0;
        while (i < j) {
            int l = q[i].l, r = q[i].r, id = q[i].id;
            while (R < r) add(a[++R], res);
            LL backup = res;//备份答案
            while (L > l) add(a[--L], res);
            ans[id] = res;
            //回滚到左指针指向当前块的右边界时的状态
            while (L < limit + 1) cnt[a[L++]]--;
            res = backup;
            i++;
        }
        memset(cnt, 0, sizeof cnt);//处理下一个块需要暴力，所有要清空cnt，最多根号n次
    }
    for (int i = 1; i <= m; i++) printf("%lld\n", ans[i]);
    return 0;
}

四、树上莫队

例题

AcWing 2534. 树上计数2

给定一棵 $N$ 个节点的树，节点编号从 $1$ 到 $N$，每个节点都有一个整数权值。

现在，我们要进行 $M$ 次询问，格式为 u v，对于每个询问你需要回答从 $u$ 到 $v$ 的路径上（包括两端点）共有多少种不同的点权值。

输入格式

第一行包含两个整数 $N,M$。

第二行包含 $N$ 个整数，其中第 $i$ 个整数表示点 $i$ 的权值。

接下来 $N−1$ 行，每行包含两个整数 $x,y$，表示点 $x$ 和点 $y$ 之间存在一条边。

最后 $M$ 行，每行包含两个整数 $u,v$，表示一个询问。

输出格式

共 $M$ 行，每行输出一个询问的答案。

数据范围

$1≤N≤40000,$
$1≤M≤10^5$
$1≤x,y,u,v≤N$
各点权值均在 $int$ 范围内。

输入样例：

8 2
105 2 9 3 8 5 7 7
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5
3 8

输出样例：

4
4

4.1 树变序列思想

这道题其实就是将基本莫队那道例题搬到了树上，求树中任意两个点之间最短路径的数字个数。对于在树上维护某些路径的信息，普遍的做法是将数转换成一个序列，此题用的是欧拉序列。

欧拉序列：

从根节点向下dfs，记录所有遇到的点，最终返回到根节点，故每个点都会在序列中出现两次。

举例：

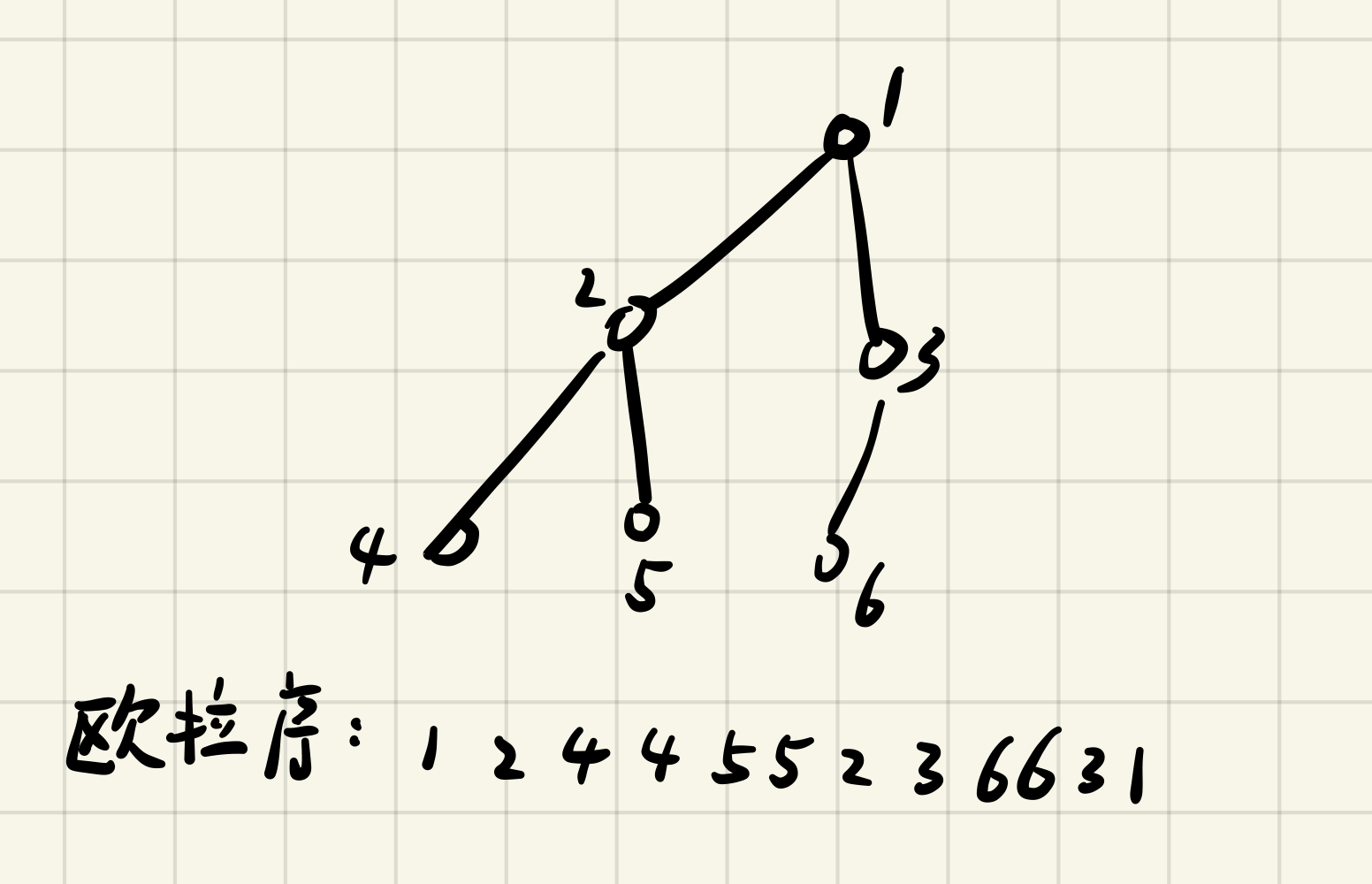
image-20210804111337834

观察上面的欧拉序列，我们可以发现这样几个性质，假设 $X$ 在欧拉序中出现地比 $Y$ 早：

  • 如果 $X$ 是 $Y$ 的祖先，那么从 $X$ 到 $Y$ 的路径上经过的节点为：欧拉序中 $X$ 第一次出现的位置到 $Y$ 第一次出现的位置的区间内只出现过一次的节点（如1到4）。
  • 如果$X$ 和 $Y$ 有一个公共祖先 $P(P\ne X ,P \ne Y)$ ，那么从 $X$ 到 $Y$ 的路径上经过的节点为：欧拉序列中 $X$ 第二次出现的位置到 $Y$ 第一次出现的位置的区间内所有只出现过一次的节点，另外再加上 $P$ ，如（4到6经过的数字在欧拉序中为4236再加上祖先1）。

如此，我们就可以将树转换成一个序列，对于每次询问，先判断 $X$ 是否为 $Y$ 的祖先，然后将询问的两个节点转变为欧拉序列中对应的下标，然后用莫队维护欧拉序列即可。当然，如果 $X$ 和 $Y$ 有一个不同于他们的公共祖先，那么还得在维护完区间后再加上他们的公共祖先。

4.2 莫队的加数操作

需要注意的是，此题莫队需要维护的是区间内只出现过一次的节点对应的数字的种数，我们用 $cnt$ 记录某个数字在区间内出现过几次，用$sta$ 标记某个节点是否在询问的路径上（如果在欧拉序中对应的区间内只出现过一次则在路径上，记为1）。我们考虑在当前序列中加入一个节点，如果这个节点当前状态 $sta = 1$ ，说明此节点之前出现过一次，现在又出现了一次，则不存在于路径上，则更新 $sta = 0$，我们可以发现加入一个节点其实就是将该节点的 $sta$ 异或上1。更新完 $sta$ 后，如果 $sta$ 变为1了，说明有新节点加入路径，则将该节点对应的数字维护到 $cnt$ 中，同时更新 $res$；如果 $sta$ 变为 0， 则删去该节点对应的数字，更新 $res$ ，代码如下：

void add(int x, int &res) {
    sta[x] ^= 1;
    if (sta[x]) {
        if (!cnt[w[x]]) res++;
        cnt[w[x]]++;
    } else {
        cnt[w[x]]--;
        if (!cnt[w[x]]) res--;
    }
}

4.3 代码

梳理一遍代码流程：

  1. 由于数字取值在 $int$ 范围，所以首先进行离散化操作。
  2. 求出树的欧拉序列。
  3. 求出每个节点的深度，同时将倍增计算lca的预处理完成。
  4. 将每次询问的两个节点转换成欧拉序的左右端点。
  5. 莫队维护计算所有询问。
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int dep[maxn], f[maxn][16], seq[maxn * 2], top, first[maxn], second[maxn];
int h[maxn], to[maxn], ne[maxn], idx;
int ans[maxn], len, n, m, w[maxn], cnt[maxn], sta[maxn];
int que[maxn], hh, tt;
vector<int> num;

void add_e(int x, int y) {
    to[idx] = y;
    ne[idx] = h[x];
    h[x] = idx++;
}
int get(int x) { return x / len; }
struct node {
    int id, l, r, p;
    bool operator<(const node &t) const {
        int a = get(l), b = get(t.l);
        if (a != b) return a < b;
        return r < t.r;
    }
} q[maxn];

void dfs(int x, int fa) {
    seq[++top] = x;
    first[x] = top;
    for (int i = h[x]; ~i; i = ne[i]) {
        int y = to[i];
        if (y == fa) continue;
        dfs(y, x);
    }
    seq[++top] = x;
    second[x] = top;
    return;
}

void bfs() {
    queue<int> q;
    q.push(1);
    dep[1] = 1;
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = to[i];
            if (dep[v]) continue;
            dep[v] = dep[u] + 1;
            f[v][0] = u;
            for (int j = 1; j <= 15; j++) f[v][j] = f[f[v][j - 1]][j - 1];
            q.push(v);
        }
    }
}

int lca(int x, int y) {
    if (dep[x] > dep[y]) swap(x, y);
    for (int i = 15; i >= 0; i--) {
        if (dep[f[y][i]] >= dep[x]) y = f[y][i];
    }
    if (x == y) return x;
    for (int i = 15; i >= 0; i--)
        if (f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}
void add(int x, int &res) {
    sta[x] ^= 1;
    if (sta[x]) {
        if (!cnt[w[x]]) res++;
        cnt[w[x]]++;
    } else {
        cnt[w[x]]--;
        if (!cnt[w[x]]) res--;
    }
}
int main(int argc, char const *argv[]) {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        scanf("%d", w + i);
        num.push_back(w[i]);
    }
    sort(num.begin(), num.end());
    num.erase(unique(num.begin(), num.end()), num.end());
    for (int i = 1; i <= n; i++)
        w[i] = lower_bound(num.begin(), num.end(), w[i]) - num.begin();
    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        add_e(a, b);
        add_e(b, a);
    }
    dfs(1, -1);
    bfs();
    for (int i = 1; i <= m; i++) {
        int a, b;
        scanf("%d %d", &a, &b);
        if (first[a] > first[b]) swap(a, b);
        int p = lca(a, b);
        if (a == p)
            q[i] = {i, first[a], first[b]};
        else
            q[i] = {i, second[a], first[b], p};
    }
    len = sqrt(top);
    sort(q + 1, q + m + 1);
    int l = 1, r = 0, res = 0;
    for (int i = 1; i <= m; i++) {
        int L = q[i].l, R = q[i].r, id = q[i].id, p = q[i].p;
        while (l < L) add(seq[l++], res);
        while (l > L) add(seq[--l], res);
        while (r < R) add(seq[++r], res);
        while (r > R) add(seq[r--], res);
        if (p) add(p, res);
        ans[id] = res;
        if (p) add(p, res);
    }
    for (int i = 1; i <= m; i++) printf("%d\n", ans[i]);
    return 0;
}

二次离线莫队

例题

Acwing 2535. 二次离线莫队

给定一个长度为 nn 的序列 $a_1,a_2,…,a_n$ 以及一个整数 $k$。

现在要进行 $m$ 次询问，每次询问给定一个区间 $[l,r]$，请你求出共有多少个数对 $(i,j)$( 满足 $l≤i<j≤r$ 且 $a_i⊕a_j$ 的结果在二进制表示下恰好有 $k$ 个 $1$。

注：$⊕$ 表示按位异或操作。

输入格式

第一行包含三个整数 $n,m,k$。

第二行包含 $n$ 个整数表示 $a_1,a_2,…,a_n$。

接下来 $m$ 行，每行包含两个整数 $l,r$，表示一次询问。

输出格式

共 $m$ 行，每行输出一个查询的结果。

数据范围

$1≤n,m≤10^5$,
$0≤k≤14$,
$0≤a_i<2^{14}$,
$1≤l<r≤n$

输入样例：

5 3 2
1 1 4 7 7
1 5
1 3
3 5

输出样例：

8
2
2

核心思想

莫队的本质其实就是调整查询的顺序使得局部查询具有单调性，从而可以用类似双指针的方式计算，但是这样可行的前提是每次指针移动后新的答案可以很快地算出来。但是遇到一些计算较为复杂的问题时，莫队就不够快了。比如例题，每移动一次指针，需要将加入（或删除）的数在整个区间内查找一次才能得到答案，是不能在 $O(1)$ 内算出的。那么我们考虑将某次询问拆分成两部分：可以通过指针移动快速算出的部分直接算出；另外一部分转移比较困难，我们可以尝试将这些修改当做某种新的询问，也都离线存下来，然后再参考莫队的思想，将这些新询问按照某种顺序快速求出，从而可以使得整体的时间不会太慢。下面以例题为例，分析一下如何处理二次离线莫队。

题目分析

我们设 $l$ 为当前的左指针， $r$ 为当前右指针，$L$ 为查询的左区间， $R$ 为查询的右区间，在某次询问的调整过程中，可能出现下面这种情形：

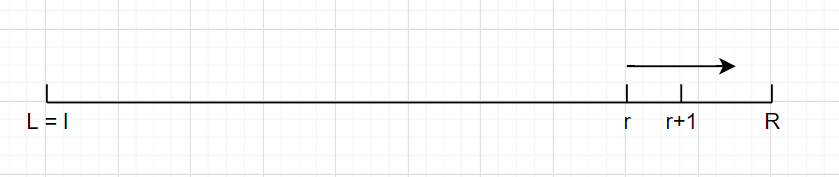
image-20210804184410420

即左指针已经对齐，右指针小于右区间，需要将右指针向右移动，我们考虑当右指针向右移动一次（到r+1时），则 $a_{r+1}$ 被加入到区间中，答案应该加上区间 $[L,R]$ 内的数字与 $a_{r+1}$ 匹配的个数。我们利用前缀和的思想：

  • 设 $S_i$ 表示从 $1$ 到 $i$ 中一共有 $S_i$ 个数与新加入（或删除）的数匹配的数。

那么新增的答案就是 $S_r – S_{l-1}$ ，我们发现 $S_r$ 算的是区间 $[1,r]$ 内与 $a_{r+1}$ 匹配的个数， $S_r$ 与新增的数之间有联系（+1的关系)，于是我们设：

  • $f[i]$ 表示：区间 $[1,i]$ 中与 $a_{i+1}$ 匹配的数，那么对于上述的情况来说，$S_r = f[r]$。

考虑如何计算 $f[r]$，根据定义我们发现，$f[i]$ 对于的区间左端点是固定的，那么我们可以从左往右预处理一遍。首先我们定义：

  • $g[x]$ 表示：当前已经统计完区间 $[1,i]$ ，数字 $x$ 有 $g[x]$ 个匹配，那么$f[i] = g[a_{i+1}]$。

由于 $0≤k≤14$, 所以我们可以先找到所有满足二进制有 $k$ 个 1 的 $y$ ，存在一个数组里。由于新加入的数只会与之前的区间产生新的匹配，假设我们已经统计完了 $[1,i-1]$ 的每个数字，现在统计$[1,i]$ 中每个数有几个匹配，只要在原来的基础上寻找 $a[i]$ 在区间内有几个匹配。假设某个数字 $x_i$ 与 $a[i]$ 匹配，那么有 $x_i \ xor\ a[i] = y_i$ ，得 $x_i = y_i \ xor \ a[i]$ ，所以只要将 $a[i]$ 与所有的 $y_i$ 异或起来，然后将 $g[y_i\ xor\ a[i]]+1$即可，再根据$S_r = f[r]$，我们就能算出所有的 $f$ 值。

下面考虑怎么算 $S_{l-1}$ ，由于它与任何东西都无关，所以不太好计算，我们根据含义：即 $[1,l-1]$ 中有几个与 $a_{r+1}$ 匹配。纵观指针 $r$ 移动到右区间 $R$ 的全过程，需要计算的 $S_{l-1}$ 有 $R-l$ 个。

  • 我们定义一个新的查询：查询某个区间 $[x,y]$ 中每个数与一个固定的区间 $[1,i]$ 匹配的数的和。

那么将题目要求的查询按照莫队的要求排好序后，对于每次查询都会有指针的左右移动，每次移动也都伴随着一次上述的新查询。于是我们将这些查询都先记录下来，然后在处理完全部查询后统一离线计算。考虑如何计算这些区间的匹配个数和：

对于这些查询，我们可以发现他们用来统计的区间 $[1,i]$ 左端点都是确定的 $1$，于是我们按照右端点递增处理，到这里我们可以发现，其实就是再计算一次 $g[x]$ 然后将此次查询涉及的数对应的 $g$ 值累加即可。这样我们 $S_{l-1}$ 的计算也完成了。

上述分析是针对右指针向右靠近右区间的情形，实际一共有四种可能的情形，下面再分析另外一种情形：

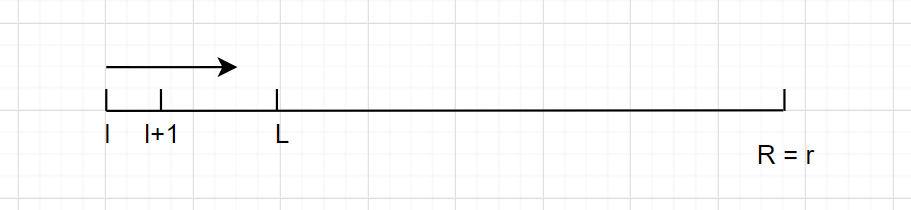
image-20210804193740149

这种情况，左指针向左移动靠近左区间，删去多余的数，那么区间的答案 $res – (S_r – S_{l})$ ,注意这里 $S_r$ 表示区间 $[1,r]$ 内有几个数与$a_l$ 匹配，注意不要把定义弄错，$S_l$ 同理。我们可以发现：$S_l$ 计算的是 $[1,l]$ 与 $a_l$ 有几个匹配，那么其实就等于 $f[l-1]$ （表示$[1,l-1]$ 内有几个与 $a_l$ 匹配）,但是区间还少一个没统计，我们额外统计一下即可，即判断 $a_l$ 是否与 $a_l$ 匹配，只有 $k = 0$ 时才匹配（二进制表示有0个1时两个相等的数才匹配）。

其他两个情况都与上述类似，不在赘述，可以参考代码！

代码模板

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int w[maxn], len, n, m, k;
LL ans[maxn];
int f[maxn], g[maxn];
int get(int x) { return x / len; }
struct Query {
    int id, l, r;
    LL res;
    bool operator<(const Query &t) const {
        int a = get(l), b = get(t.l);
        if (a != b) return a < b;
        return r < t.r;
    }
} q[maxn];
struct Range {
    int id, l, r, op;
};
vector<Range> range[maxn];
vector<int> num;

int count_num(int x) {
    int res = 0;
    while (x) res += x & 1, x >>= 1;
    return res;
}

int main(int argc, char const *argv[]) {
    cin >> n >> m >> k;
    for (int i = 0; i < (1 << 14); i++) {
        if (count_num(i) == k) num.push_back(i);
    }
    for (int i = 1; i <= n; i++) scanf("%d", w + i);
    for (int i = 1; i <= n; i++) {
        for (auto y : num) g[w[i] ^ y]++;//g[x] 表示1-i中有几个数与x匹配
        f[i] = g[w[i + 1]];//f[i] 表示1-i中有几个数与w[i+1]匹配
    }
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &q[i].l, &q[i].r);
        q[i].id = i;
    }
    len = sqrt(n);
    sort(q, q + m);
    int l = 1, r = 0;
    for (int i = 0; i < m; i++) {
        int L = q[i].l, R = q[i].r;
        if (r < R) range[l - 1].push_back({i, r + 1, R, -1});//记录需要二次离线的区间
        while (r < R) q[i].res += f[r++];//可以直接维护的区间直接计算
        if (r > R) range[l - 1].push_back({i, R + 1, r, 1});
        while (r > R) q[i].res -= f[--r];
        if (l < L) range[R].push_back({i, l, L - 1, -1});
        while (l < L) q[i].res += f[l - 1] + !k, l++;
        if (l > L) range[R].push_back({i, L, l - 1, 1});
        while (l > L) q[i].res -= f[l - 2] + !k, l--;
    }
    memset(g, 0, sizeof g);
    for (int i = 1; i <= n; i++) {//枚举区间长度为1到i的每个区间
        for (auto y : num) g[w[i] ^ y]++;//g[x]表示和上述相同
        for (auto rg : range[i]) {//找到所有区间为1-i的询问
            int id = rg.id, l = rg.l, r = rg.r;//此询问查找的区间
            for (int x = l; x <= r; x++) q[id].res += g[w[x]] * rg.op;//将对应的值加入
        }
    }
    for (int i = 1; i < m; i++) q[i].res += q[i - 1].res;//前缀和思想将变化量算成真的答案
    for (int i = 0; i < m; i++) ans[q[i].id] = q[i].res;
    for (int i = 0; i < m; i++) printf("%lld\n", ans[i]);
    return 0;
}
莫队

评论

  1. fj
    Windows Chrome
    2 年前
    2022-3-24 19:26:58

    tql

  4. fj
    Windows Chrome
    已编辑
    2 年前
    2022-3-24 19:30:40

    2.2 带回滚的莫队思想 里面第七行“然后将指针向右移动将所有”应该是“向左移动”吧~~|´・ω・)ノ

发送评论 编辑评论 

































































































|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
 




颜文字
Emoji
小恐龙
花!
 


 














上一篇
下一篇 




推荐文章





Codeforces Round #754 (Div. 2) C-E





Edu Codeforces Round 115 (Div. 2)





SDUT 2021 Autumn Individual Contest – D





KMP与AC自动机详细讲解（带图）





2021牛客暑期多校训练营5 J Jewels