| # | Name | ||
|---|---|---|---|
| A | A.M. Deviation | ||
| B | Reverse Sort | ||
| C | Dominant Character | ||
| D | Treelabeling | ||
| E | Array Equalizer | ||
| F | PalindORme |
C. Dominant Character(暴力+剪枝、思维)
题意
给你一个只含有’a’, b’, ‘c’ 的字符串,长度1e5内,让你寻找最短的子串满足:
- 长度大于等于2
- ‘a’ 的个数严格大于 ‘b’ 的个数
- ‘a’ 的个属于严格大于 ‘c’ 的个数。
思路
暴力做法,从每个位置开始往后找,寻找到第一个满足条件的子串,所有位置的最短子串为答案,复杂度为 $O(n^2)$ ,考虑剪枝,从每个位置开始寻找,当 ‘b’ 和 ‘c’ 的个数大于 ‘a’ 的个数时,就break掉,因为肯定不是最优的解或者解不存在。
代码
#include <bits/stdc++.h>
const int maxn = 1e6 + 10;
const int inf = 0x3f3f3f3f;
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
char s[maxn];
struct node {
int b, c, pos;
};
vector<node> cnt;
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
int n;
cnt.clear();
cin >> n;
cin >> s;
int st;
int i = 0;
while (i < n && s[i] != 'a') i++;
cnt.push_back({0,0,i});
i++;
int tot[4] = {0, 0, 0};
while (i < n) {
if (s[i] == 'a') {
cnt.push_back({tot[1], tot[2], i});
tot[1] = tot[2] = 0;
} else {
tot[s[i] - 'a']++;
}
i++;
}
int ans = inf;
for(int j = 0; j < cnt.size(); j++) {
int a = 1;
tot[1] = tot[2] = 0;
st = cnt[j].pos;
for (int i = j+1; i < cnt.size(); i++) {
if (a + 1 < tot[1] + cnt[i].b || a + 1 < tot[2] + cnt[i].c) {
break;
} else if (a + 1 > tot[1] + cnt[i].b &&
a + 1 > tot[2] + cnt[i].c &&
cnt[i].pos - st + 1 >= 2) {
ans = min(ans, cnt[i].pos - st + 1);
break;
} else {
tot[1] += cnt[i].b;
tot[2] += cnt[i].c;
a++;
}
}
}
if (ans == inf)
puts("-1");
else
printf("%d\n", ans);
}
return 0;
}
D. Treelabeling(构造+博弈)
题意
Eikooc 和 Sushi 玩游戏,有一棵编号从 $1$ 到 $n$ 的树,两个人轮流操作,Eikooc先手。除了第一次可以任意选择外,假设上一轮对手选择的点为 $v$ ,则次轮可以选择的点 $v$ 需要满足:
- $u$ 与 $v$ 相邻。
- $u$ 没被访问过
u ^ v <= min(u,v),其中^表示异或。
Eikooc可以将树上的点重新排列,需要输出一个 1 到 $n$ 的排列 $p$ ,$p_i$ 表示第 $i$ 个节点重新排列后的标号,要求重新排列后Eikooc 在游戏开始时可以选择的必胜点最多,必胜点表示若Eikooc第一次选择该点,则无论Sushi如何操作,Eikooc都必胜,若有多种解,输出任意一种即可。
思路
考虑什么情况下不能满足 u ^ v <= min(u,v) 。根据异或的特性可以知道,只要两个数字的最高位不同,则异或出来的数字一定比两者的最小值大。考虑是否可以构造一种方案使得每个点和相邻点的最高位都不同。我们可以按照每个点所在层数的奇偶将点分成两类,只要奇数层的点和偶数层的点之间没有两个点的最高位相同即可。先求出1-n每个数的最高位,然后每次将最高位相同的数字分配给奇数层中的节点或者偶数层的节点。分配时,若当前偶数层中的节点多则将相同最高位的数字都分配给偶数层,否则分配给奇数层。根据二进制的性质可以知道,一定可以完成分配。
代码
#include <bits/stdc++.h>
const int maxn = 1e6 + 10;
const int inf = 0x3f3f3f3f;
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
vector<int> mp[maxn], be[2];
int ans[maxn], top[maxn];
void dfs(int now, int fa, int x) {
be[x].push_back(now);
for (int i = 0; i < mp[now].size(); i++) {
if (mp[now][i] == fa) continue;
dfs(mp[now][i], now, x ^ 1);
}
}
void init() {
int cnt = 1, ne = 1, mi = 1;
for (int i = 1; i < maxn; i++) {
top[i] = mi;
cnt--;
if (cnt == 0) {
ne *= 2;
cnt = ne;
mi++;
}
}
}
vector<int> v[20];
int main(int argc, char const *argv[]) {
int t;
init();
cin >> t;
while (t--) {
int n;
cin >> n;
int li = 2, mi = 0, i = 1;
for (int i = 0; i <= n; i++) mp[i].clear();
for(int i = 0; i < 20; i++) v[i].clear();
be[1].clear();
be[0].clear();
for (int i = 0; i < n - 1; i++) {
int u, v;
scanf("%d %d", &u, &v);
mp[u].push_back(v);
mp[v].push_back(u);
}
dfs(1, 0, 0);
for (int i = 1; i <= n; i++) v[top[i]].push_back(i);
int now = 0;
for (int i = 20; i >= 0; i--) {
if (be[now].size() < be[now ^ 1].size()) now ^= 1;
for (auto it : v[i]) {
ans[be[now].back()] = it;
be[now].pop_back();
}
}
for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
puts("");
}
return 0;
}
E. Array Equalizer
题意
有两个长度为 $n$ 的数组 $a$ 和 $b $ ,有以下两种操作:
- 选择 $1-n$ 中的任意一个数字 $i$ ,然后将数组中下标为 $i$ 以及 $i$ 的倍数的数字都 +1。
- 选择 $1-n$ 中的任意一个数字 $i$ ,然后将数组中下标为 $i$ 以及 $i$ 的倍数的数字都 -1。
有 $q$ 次查询,每次将 $b_1$ 变为 $x$ ,问最少的操作次数使得 $a$ 变为 $b$ 。
思路
由于每次操作都是将某些数字一起进行加或减,且都是将某个数以及它后面的数一起加减,所以如果要改变一个数的值只能对这个数进行操作,即操作顺序不会影响操作次数,只要从第一个数字开始,每次使得 $a_i$ 变为 $b_i$ 同时更新后面受影响的值,这样计算就是某次情况的最优解。另外,从 $a$ 变为 $b$ 可以转变成将一个全为0的数组 $A$ 变为数组 $B$ ,其中 $B_i = b_i – a_i$,下面全用 $A$ 和 $B $ 来代替,模拟操作如下:

其中 add 表示对于每个数字需要加减的数值,即add的绝对值表示操作次数(负数表示减add次,正数表示加add次)。一开始将 $A_1$ 变为 $B_1$ ,需要加 $B_1$ 次(这里的加不一定是加,如果$B_1$ 为负数则为减,下同),相应的,所有 $1$ 的倍数都加了 $B_1$ ,如上图第二段所示。然后将 $A_2$ 变为 $B_2$ ,需要加 $B_2 – B_1$ 次,同时下标为 $2$ 的倍数的数字也都加上 $B_2 – B_1$ ,故 $A_4$ 和 $A_6$ 的值变为 $B_2$,依次操作。
由于每次询问改变了 $b_1$ 的值,可以将 $B_1 = b_1 – a_1$ 设为 $x$ ,则最后的add分别为:
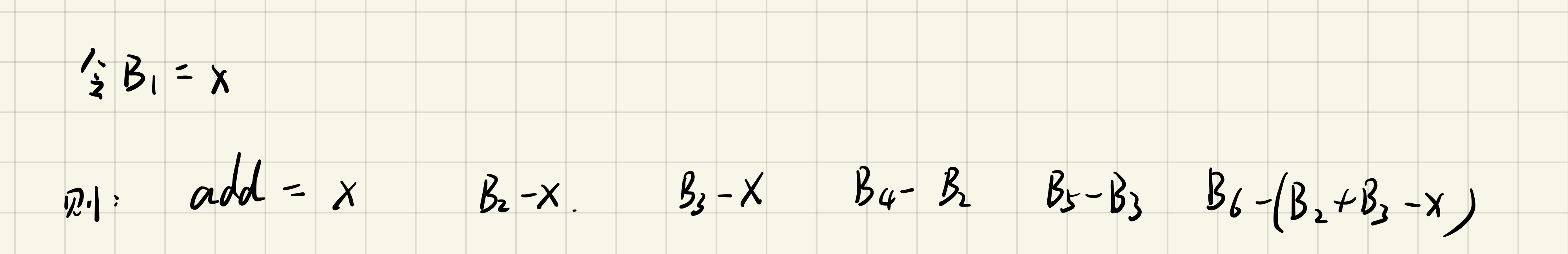
可以发现 add 其实就是一个 $cx + d$ 的一次方程,其次 $x$ 为未知数,$c$ 和 $d$ 为可以计算得到的常数。最终需要我们计算的就是 $|cx+d|$ ,假设 $c$ 为正数(如果不为正数则将整体取相反数即可,答案计算的是绝对值,所以不会有影响),易知 $x < -\frac d c$ 时$|cx+d| = -(cx+d)$。所以我们可以求出每个add的 $-\frac dc$ ,放入一个桶中,然后计算前缀和,每次询问 $O(1)$ 得出。还有一些细节,比如 $c$ 为 0时的处理,以及 $-\frac cd$ 为负数时的处理,具体看代码。
代码
#include <bits/stdc++.h>
const int maxn = 2e5 + 10;
const int base = 2e6 + 10;
const int inf = 0x3f3f3f3f;
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int a[maxn];
PLL add[maxn];
PLL sum[2 * base + 10];
int main(int argc, char const *argv[]) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) scanf("%d", a + i);
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
if (i > 1) a[i] = x - a[i];
}
add[1] = {1, 0};
for (int i = 1; i <= n; i++) {
if (i > 1) add[i].second += a[i];
for (int j = 2 * i; j <= n; j += i) {
add[j].first -= add[i].first;
add[j].second -= add[i].second;
}
if (add[i].first < 0) {
add[i].first = -add[i].first;
add[i].second = -add[i].second;
}
}
LL ans = 0;
for (int i = 1; i <= n; i++) {
if (add[i].first == 0) { // 斜率为0,则不受x的影响,直接加到答案上即可
ans += abs(add[i].second);
continue;
}
int pos = ceil(-add[i].second * 1.0 / add[i].first);
//由于x的取值为1e6内,所以超出1e6的可以直接放到两端即可
pos = max(-base, pos);
pos = min(pos, base);
pos += base; // pos 可能为负数加上偏移量
sum[pos].first += add[i].first;
sum[pos].second += add[i].second;
}
for (int i = 1; i <= 2 * base; i++) {
sum[i].first += sum[i - 1].first;
sum[i].second += sum[i - 1].second;
}
int q;
cin >> q;
while (q--) {
int x;
cin >> x;
x -= a[1];
printf("%lld\n", ans + sum[x + base].first * x + sum[x + base].second -
((sum[2 * base].first - sum[x + base].first) * x +
sum[2 * base].second - sum[x + base].second));
}
return 0;
}
