零、程序语言的定义

一个程序语言是一个记号系统，其定义包含两部分：语法和语义

0.1 语法

语法：形成和产生合适程序的规则集，描述了该语言的程序的正确形式。

词法规则：形成单词符号的规则
语法规则：形成语法单位的规则（语法树表示）

常用的语法描述方法（文法）：

用正规文法描述词法规则。
用上下文无关文法描述语法规则。

0.2 语义

语义：用以定义程序意义的规则集，即解释程序在运行时做什么

静态语义：标识符未声明、重复声明、类型不符、种类不符

动态语义：除零错误、下标越界、无效指针、死循环

在不同语言中完全相同的语法单位，含义却可能完全不同，例如：x=y 在C语言中表示赋值表达式，在Pascal语言中为关系表达式。

一、文法的直观概念

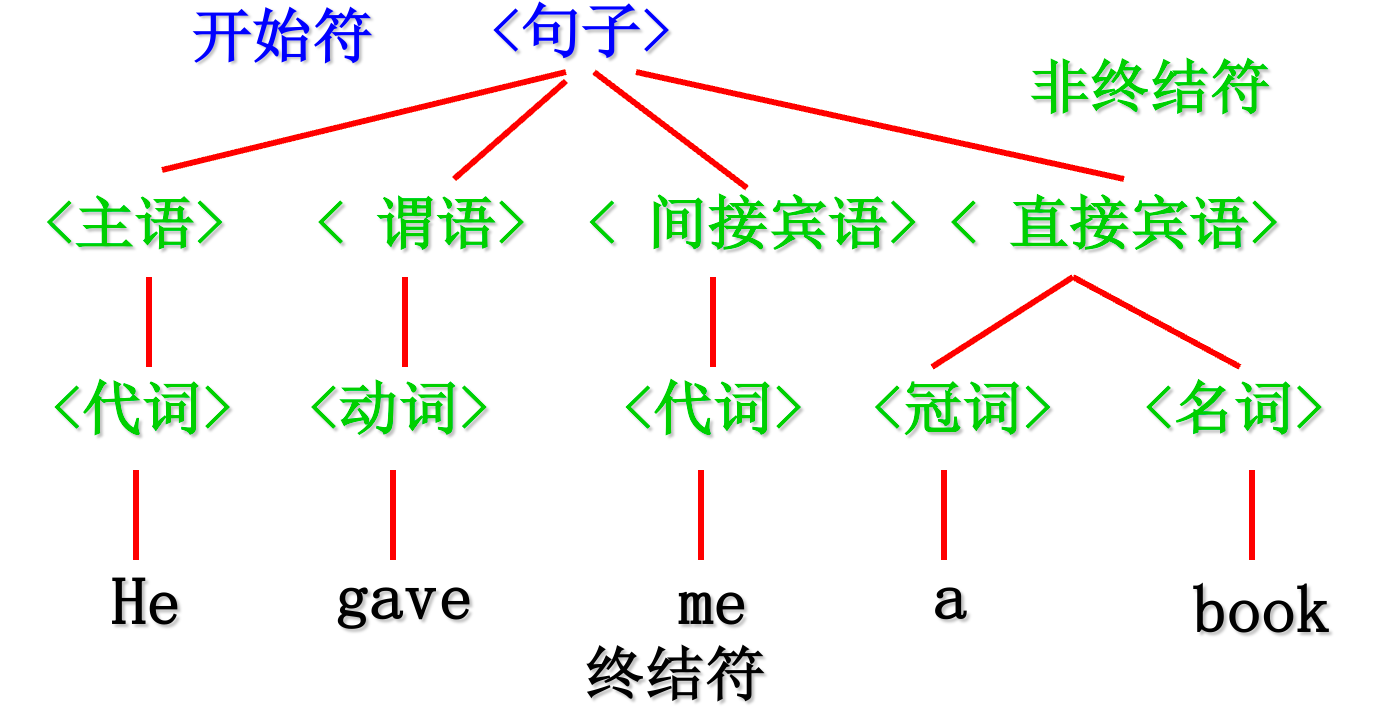
以定义描述英语句子的文法为例：He gave me a book

文法的规则如下：

(1)<句子>→<主语><谓语><间接宾语><直接宾语>
(2)<主语>→<代词>
(3)<谓语>→<动词>
(4)<间接宾语>→<代词>
(5)<直接宾语>→<冠词> <名词>
(6)<代词>→He|me
(7)<冠词>→a
(8)<动词>→gave
(9)<名词>→book|peach

< > 表示该对象还需要进一步定义， -> 表示将左边的定义为右边。

应用上述语法规则进行推导：

句子
=>主语 谓语 间接宾语 直接宾语
=>代词 谓语 间接宾语 直接宾语
=>He 谓语 间接宾语 直接宾语
=>He 动词 间接宾语 直接宾语
=>He gave 间接宾语 直接宾语
=>He gave 代词 直接宾语
=>He gave me 直接宾语
=> He gave me 冠词 名词
=> He gave me a 名词
=> He gave me a book

=> 表示应用某个规则进行推导（即将相应规则的右部进行替换），上述例子中，终结符号为He,me,book,gave等，非终结符号为句子,主语,谓语,动词等，开始符号为 句子，产生式依靠语法规则。

画出语法树：

二、符号和符号串

2.1 符号和字母表

符号(元素)： 可以相互区别的记号，例如 a b 0 1。

字母表： 符号的非空有穷集合，如 {0,1} 表示二进制数语言的字母表，程序设计语言的字母表是该语言的基本字符集。

C语言是C程序的集合，C程序是在C基本字符集上定义的，按一定规则构成的符号串。

2.2 符号串

定义：由字母表中的符号所组成的任何有穷序列称为该字母表上的符号串。

空串： (ε—空字) 长度为0的符号串，|ε|=0。

2.2.1 符号串的操作

运算：

连接（并置）：x = 123, y = 45, xy = 12345
方幂：$x^0 = ε,x^1 = x, x ^ 2 = xx…$

子字符串： 非空，原串从头和尾去掉 $\ge0$ 个字符得到。

头，尾： x是xy的头，y是xy的尾。

2.2.2 字符串集合

定义：若集合A中的一切元素都是某字母表上的符号串，则称A为该字母表上的符号串的集合。

例： $∑={0，1}$ 是字母表,其中 0,1 为符号，则$D={0,1}$ 其中 0,1 为符号串，$E= {ε, 0,1,00,01,10,11,000, …}$是 $∑$ 上的符号串集合。特别：空集记为$ф ={\ }$ 注意与 $ε$ 区别。

操作：

乘积： $UV = {αβ|α∈U且β∈V}$
方幂：V的n次方幂就是将n个V相乘
符号串集V的闭包 $V^* =V^0∪ V^1 ∪ V^2 ∪ V^3 ∪… $，，即 V 上的所有符号串(包括空字ε)的集合。
符号串集V的闭包 $V^+ =V^1 ∪ V^2 ∪ V^3 ∪… $，，即 V 上的所有非空符号串(包括空字ε)的集合。

2.2.3 语言的概念

某个字母表 $∑$ 上的符号串集合，是 $∑^*$ 的一个子集。

三、文法和语言的形式定义（重点）

3.1 规则或产生式

形式: $α→β$或$α::=β$，α 称为产生式的左部，β称为产生式的右部，读作“α定义为β”。

举例：

A→a 这是关于A的一条规则
<标识符> →<字母>
<字母> →a|b|……|z

3.2 文法的定义

定义：$Ｇ = (Ｖ_T，Ｖ_N，S，P)$，以四元式的形式表示。

$Ｖ_T$ 非空有穷终结符集

$Ｖ_N$ 非空有穷非终结符集 $Ｖ_T ∩Ｖ_N = ф $

$S∈Ｖ_N$ 开始符号，S至少在产生式左部出现一次

$P$ 非空有穷产生式集合 $α→β$

$α∈(Ｖ_T ∪Ｖ_N)^*$，且至少含有一个非终结符
$β∈(Ｖ_T ∪Ｖ_N)^*$，

令$Ｖ=Ｖ_T ∪Ｖ_N$ ，称Ｖ为文法符号，是文法G的字母表

3.3 文法描述的约定

用大写字母A、B、C…或汉语词组<标识符>代表非终结符号

用小写字母a、b、c…代表终结符号

用希腊字母α、β、γ…代表终结符号和非终结符号组成的符号串

若干个左部相同的产生式可以合并为一个 $P→α_1| α_2 |…| α_n$，每个αi 称为P的一个候选式

3.4 推导

直接推导：

产生式右部代替左部，当$Ａ→γ$ 是文法Ｇ的一个产生式，且$α、β∈(Ｖ_T∪Ｖ_N)^*$，则有$α\ Ａ\ β => α\ γ\ β$，称 $α\ γ\ β$ 是 $α\ Ａ\ β$的直接推导或称 α γ β 直接归约到 αＡβ ，$G[E]:E→E + E|E * E|( E )|i，i + E => i + E * E$

特点：只能用一次产生式替换。

归约：

如果$α_0=>α_1=>α_2=>…=>α_n$，则称这个序列是从$α_0$至$α_n$的一个推导

用$α_0=^+>α_n$表示从 $α_0$ 出发，经一步或多步推导，可推出 $α_n$

用 $α_0=^*>α_n$ 表示从 $α_0$ 出发，经零步或多步推导，可推出 $α_n$ ，即 $α_0=α_n或α_0=^+>α_n$

3.5 句型

定义：设 G 是一个文法，S 是开始符号，若有 $S =^*>α$，则称 α 是文法 G 的一个句型。$G(E):E→E + E|E * E|( E )|i$。

例如 $E=+>iE$,则 $E$ 是文法 $G(E)$ 的一个句型。

$E=^+>ii$,则 $ii$ 是文法 $G(E)$ 的一个句型。

句子：完全由终结符组成的句型。例如 $E=^+>ii$,则 $ii$ 是文法 $G(E)$ 的一个句子。

合法句子的生成：u从Ｓ出发反复推导，每次得到一个句型，最终得到句子。

3.6 文法G描述的语言

由文法Ｇ产生的所有句子的集合为：$Ｌ(Ｇ)＝{α｜Ｓ＝^+＞α \ 且\ α∈Ｖ_T^*}$

文法G的作用：以有限的规则描述无限的语言现象。

有限：产生式集合、终结符集合、非终结符集合。
无限：由开始符号导出的句子。

例：$G[E]:E→E + E|E * E|( E )|i$，文法G所描述的语言：含有+、*和括号的算术表达式

3.7 文法等价性

若L(G1)=L(G2)，则称文法G1和G2是等价的（它们产生的句子集合相同）

例子：

文法 $G_1[E]:E→E+E | E*E |(E)| i $$

文法 $G_2[E]:E→E+T | T$，$T→T*F | F$，$F→(E)| i$

因为$L(G_1)=L(G_2)$,所以文法$G_1$和$G_2$是等价的。

四、文法的类型

4.1 0型文法（短语文法）

对任一产生式$α→β$，都有$α∈(Ｖ_N∪Ｖ_T)^*$且α至少含有一个非终结符，$β∈(Ｖ_N∪Ｖ_T)^*$，此类文法的限制最少，描述能力最强。

4.2 1型文法（上下文有关文法）

对任一产生式$α→β$，都有$|α|≤|β|$ 仅仅$Ｓ→ε$ 除外，并且Ｓ不出现在其他产生式的右部。

例如： S→aSBA，AA’→AB 。

这里的上下文有关指的是，对于某个推导还限制了一定的条件，比如 $AA’→AB$ ，直观来看就是 $A’→B$，但是替换有个“上下文限制”，即必须前面有一个 $A$ 才能替换。

4.3 2型文法（上下文无关文法）

对任一产生式α→β，都有$α∈Ｖ_N，β∈(Ｖ_N∪Ｖ_T)^*$

例如 $E→E+T|T$，足以描述大多数程序设计语言语法特征

4.4 3型文法（正规文法）

右线性文法：对任一产生式的形式都为Ａ→ａＢ或Ａ→ａ，其中$Ａ，Ｂ∈Ｖ_N ，ａ∈Ｖ_T^* （ａ可为ε）$
左线性文法：对任一产生式的形式都为Ａ→Ｂａ或Ａ→ａ，其中$Ａ，Ｂ∈Ｖ_N ，ａ∈Ｖ_T^* （ａ可为ε）$

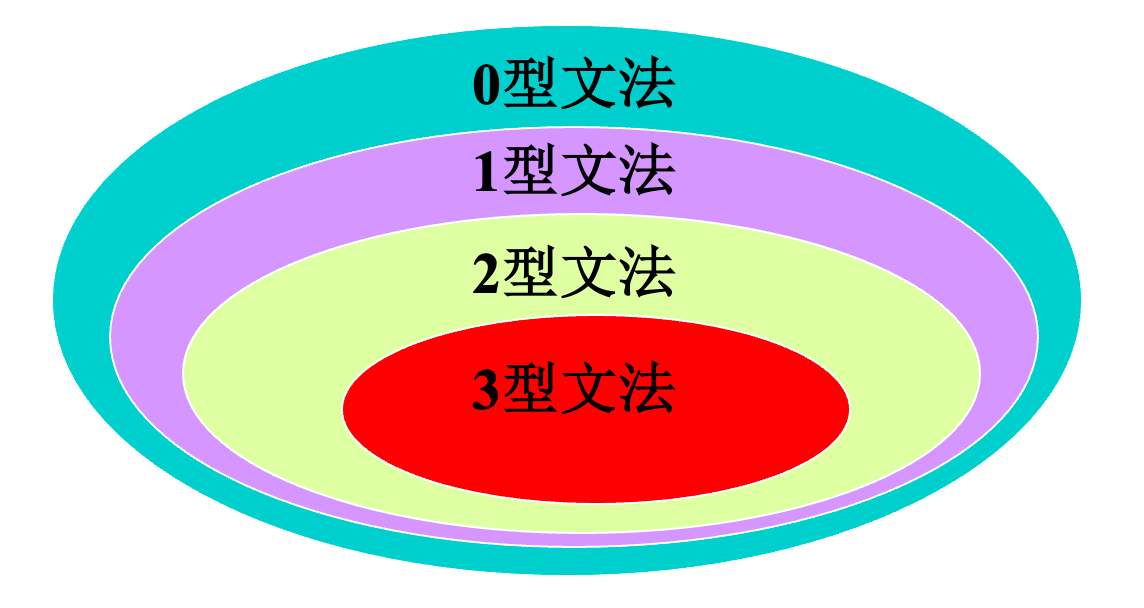
4.5 四类文法的关系

由于四种文法是按照将产生式做进一步限制而定义的，所以它们之间是逐级“包含”的关系，由四种文法产生的语言也是逐级“包含”关系。

五、上下文无关文法及其语法树（重点）

5.1 上下文无关文法组成

终结符号：组成语言的基本符号，在程序语言中是单词符号。

非终结符号：用来代表语法范畴(语法概念)，每个非终结符号表示一定符号串的集合。

开始符号：一个特殊的非终结符号。

产生式：是定义语法范畴的一种书写规则。形式 A→α，A是一个非终结符，称为产生式的左部符号，α是一个符号串，称为产生式的右部

5.2 语法树（推导树）

构造特点：

每个结点都有一个V中的符号作标记
根结点——开始符S
中间结点——非终结符 $A∈Ｖ_N$
叶结点——非终结符或终结符(关于句型)，终结符$a∈Ｖ_T $(关于句子)
如果结点n标记为A，其直接子孙从左到右的标记为$A_1,A_2,…,A_k, 则 A→ A_1A_2…A_k ∈P$

构造步骤：

步骤1 根结点为开始符号
步骤2 对于每一次推导使用的产生式A→α，找出A对应的结点(此时应该是末端结点)，从该结点向下画分支，子结点从左到右分别是α中从左到右的符号
重复步骤2直到推导的最后一步

语法树特点：

从语法树的构造过程可以看出，句型的推导过程不同，语法树的生长过程也不同，但最终生成的语法树结构是完全相同的。可以说，一棵语法树包括了一个句型所有可能的推导过程。整体上看不出推导的次序(即产生式使用的次序)，只能看出使用了哪些产生式。

5.3 最左（最右）推导

定义：在一个推导的过程中，如果每一步直接推导所被替换的总是最左(右)的非终结符号。最右推导常被称为规范推导。由规范推导所得到的句型称为规范句型，也称为右句型。

5.4 二义性文法

5.4.1 二义性定义

若一个文法存在某个句型对应两棵不同的语法树，则称这个文法是二义性文法。或者，若一个文法存在某个句型有两个不同的最左(最右)推导，则称这个文法是二义性文法。二义性一般是有害的，如果一个句子具有二义性，那么对这个句子的结构可能有多种“正确”的解释。通常情况下，我们希望对每个语句的分析是唯一的。但是,只要我们能够控制和驾驭文法的二义性,文法二义性的存在并不一定是坏事。

例如：文法$G：E→E+E | EE | (E) | i$，文法的句子: $i+ii$，其语法树如下：

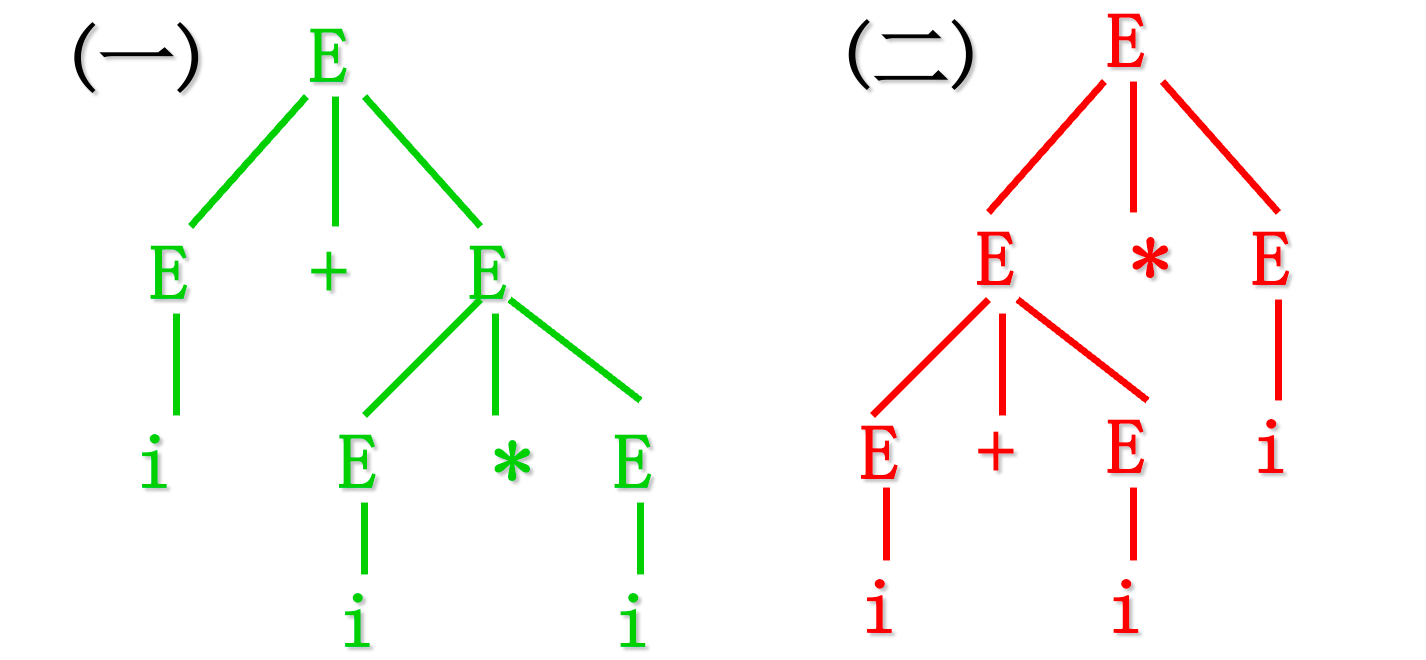
5.4.2 二义性的判定

这个问题是不可判定的。对某文法，若能找出一个句子对应两棵不同的语法树，则该文法必是二义性文法。

二义性文法可以改造为无二义性文法。

$G1[E]: E → E + E | E * E|( E )|i $，G1是二义性文法

$G2[E]: E → E+T|T，T → T*F|F，F →(E)|i$，G2(E)是无二义性文法，两者等价。

六、句型的分析（重点）

6.1 基本概念

句型分析问题：如何知道所给定的字符串是文法的句型。

句型的分析：就是识别一个符号串是否为某文法的句型，是某个推导的构造过程。或者说，是否能为一个符号串构造一颗语法树。

语法分析树（或分析树）：就是语法树。

分析程序（或识别程序）：完成句型分析的程序。分析算法又称为识别算法。

6.2 自上而下的分析方法

从开始符号出发，构造最左推导的过程。即从树根出发，利用推导生成语法树的过程。

例如：

文法$G[S]: (1) S→cAd \ \ (2)A→ab \ \ (3)A→a$，输入串$w=cabd$

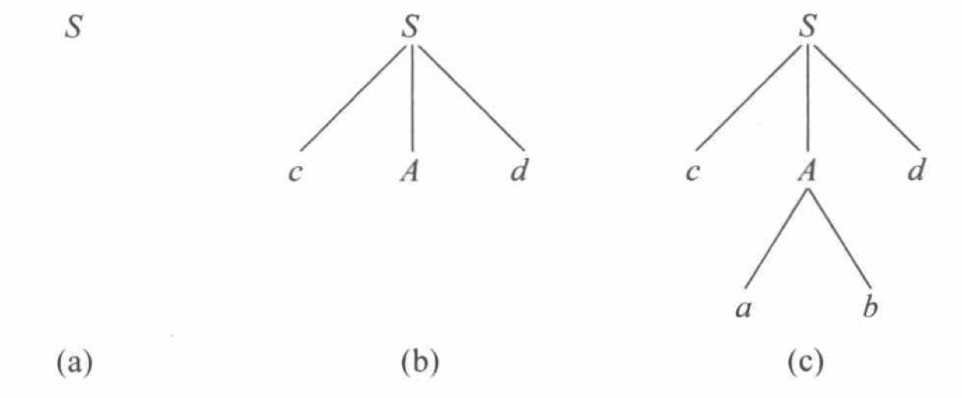
6.3 自下而上的分析方法

从输入串出发，进行最左归约，直到开始符号。从叶子结点出发，修剪语法树直至只剩开始符。

还是以上面的文法为例：

首先选择$ab$，然后用A替换，即把 $ab$ 归约到 $A$。

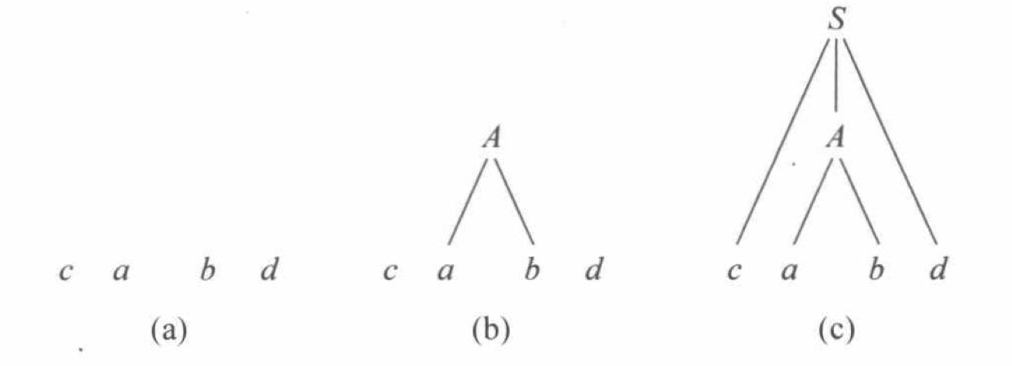
6.4 句型分析的有关问题

6.4.1 自上而下的句型分析

文法$G[S]: (1) S→cAd \ \ (2)A→ab \ \ (3)A→a$，输入串$w=cabd$，根据自上而下的推导，我们构造出第一个直接推导$S\Rightarrow cAd$，接着拓展非终结符$A$ ，这时有多种选择，如果我们用产生式（3）推导，我们可以发现构造不出$w = cabd$ ，所以是个错误推导。面对这种情况，需要退回去，试试另外一种选择，这种方式称为回溯，但是这种方法效率极低。

6.4.2 自下而上的句型分析

在归约的时候，同样也会遇到多种选择的情况，如果用（3）将 a 归约成 A，则会出错，必须用（2）进行归约。在一种叫做规范归约的分析方法中，我们将这些能够正确归约的子串称为可归约串，也称为句柄。

下面介绍三个重要的概念：

$\overset*\Rightarrow$ 指左部可以经过0步或多步推导得到右部，$\overset+\Rightarrow$ 指左部可以经过1步或多步推导得到右部

短语： 若$Ｓ\overset*\Rightarrow αＡδ，且A\overset+\Rightarrowβ$，则称 $β$ 是句型 $αβδ$ 相对于非终结符号 A 的短语。
直接短语：若$Ｓ\overset*\Rightarrow αＡδ 且 A\Rightarrowβ$，则称β是句型 αβδ 相对于非终结符号A的直接短语。
句柄： 一个句型的最左直接短语称为该句型的句柄。（此概念只适用于右句型）

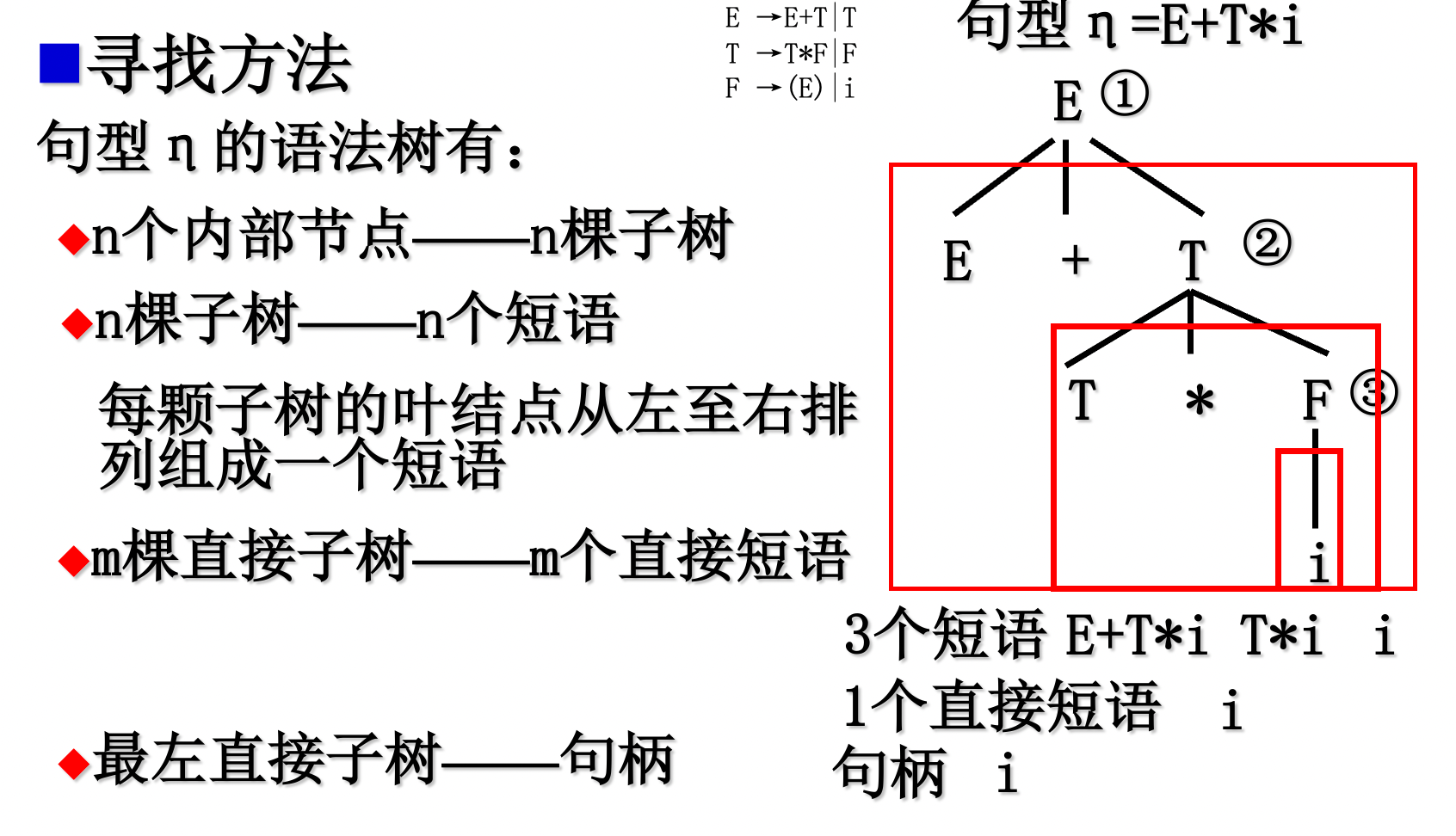
6.4.3 利用语法树寻找短语、句柄等方法

句型η的语法树有若干个内部节点（包括根节点）每个内部节点对应一棵以该内部节点为根的子树。

如果一棵子树只有父子两代（两层节点），则称该子树为直接子树。

如果一棵子树的根标记为A，且将此子树的叶节点标记自左至右排列所形成的符号串为β，则β是句型 η 相对于A的一个短语。

如果子树是一棵直接子树，则β是句型 η 相对于A的一个直接短语，最左直接子树对应该句型的句柄。

零、 程序语言的定义