一、机器学习分类

1.1 监督学习

给出一组数据及正确的答案，使用数据训练出一个模型，当有新数据时可以得到正确结果。

• 回归问题：预测连续值的属性(如房价预测等)；
• 分类问题： 将无穷多的特征进行分类，即预测离散型输出（如根据一些信息判断肿瘤是否为恶性）。

1.2 无监督学习

给出大量数据，不给出正确的答案 ，让机器自己寻找数据中可能的类型结构。

• 聚类：将一组数据进行分类，不预先说明有哪些类别。
• 鸡尾酒会算法：混合音频的分离。

二、单变量线性回归

2.1 模型描述

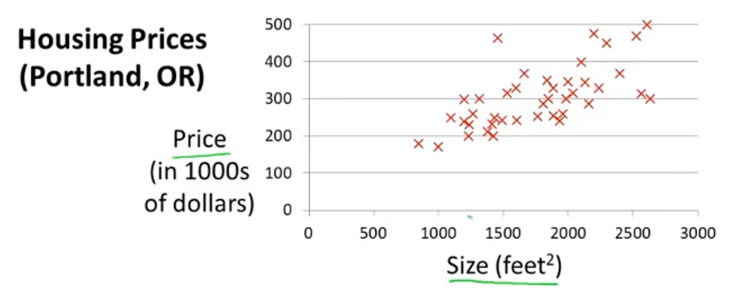
如图表示一个房价预测的数据集，x轴表示房子的面积，y轴表示对应的房价，现在需要做的就是用一条直线拟合这些数据，使得给出一个新的房子面积，可以预测出它的房价。当然，可以用曲线来拟合数据使得预测更加准确，但是目前只先讨论单变量的线性回归，即用直线来拟合数据。

定义一个数据集：

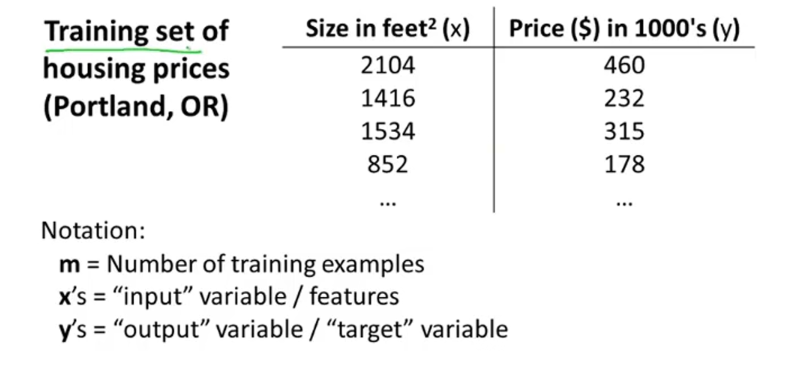
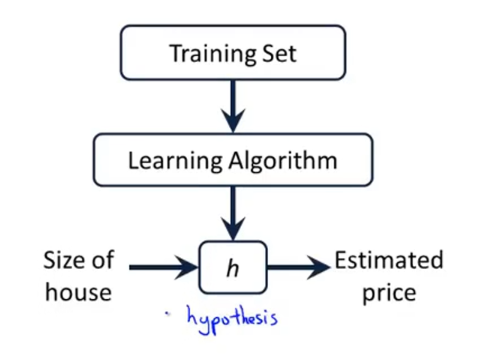
假设有如图所示的数据，称为一个训练集，其中用 $m$ 表示 数据集的大小，用 $X^{(i)}$ 表示第 i 行的输入（即房子面积），用 $Y^{(i)}$ 表示第 i 行的输出（房价）。用训练集进行训练，可以得到一个假设函数 $h$ ，通过 $h$ 可以建立一个从 $X$ 到 $Y$ 的映射。对于单变量的线性回归，我们这样表示假设函数 ：$h_{\theta}(x) = \theta_0 + \theta_1x$​

2.2 代价函数

假设函数 ：$h_{\theta}(x) = \theta_0 + \theta_1x$

我们称 $\theta_0$​​ 和 $\theta_1$​​ 为模型参数，目的是找到合适的 $\theta_0 \theta_1$​​最小化$\frac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)}) - y^{(i)})^2$​​，m指训练集的样本容量，（即预测值和实际值的差的平方再求和），这就是代价函数，记作$J(\theta_0,\theta_1)=\frac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)}) - y^{(i)})^2$​​​,也被称为误差平方函数，是解决线性回归问题最常用的代价函数，到此为止，我们一共定义了假设函数，模型参数，代价函数，并且知道了线性回归的目的是 $\underset {\theta_0,\theta_1} {minimize} \ J(\theta_0,\theta_1)$​​​。

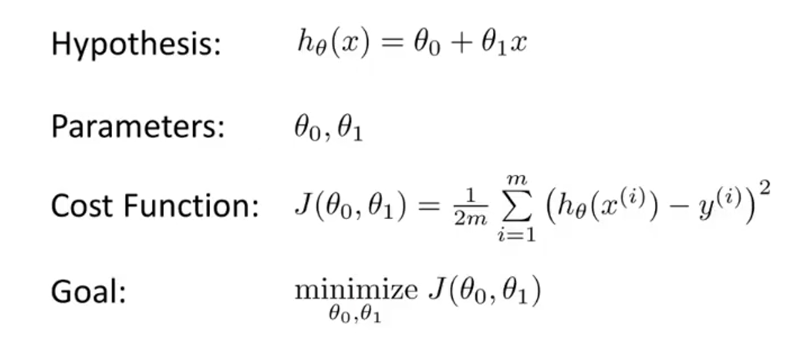
如果将函数简化成 $J(\theta_1)$ ，即 $\theta_0 = 0$ ，那么$h_{\theta}(x)$ 就是一条经过原点的直线（如下图左），假设我们有三个样本（左图红×处），不断改变 $\theta_1$ 的取值，计算代价函数，可以得到下图右边这样的一个函数，可知，$\theta_1 = 1$ 时，代价函数值最小。

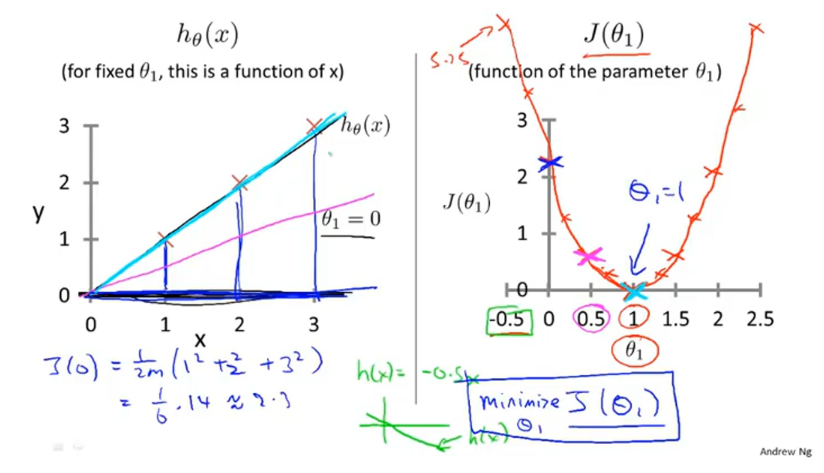
如果再加入 $\theta_0$​ 的影响，由于有两个参数的影响，所以所以 $J(\theta_0,\theta_1)$​ 为一个三维图形，如下图左，将三维图形画成等高线图，可得到右边的两张图，可以直观看出，当取值为椭圆的中心点时，代价函数取值最低：

 

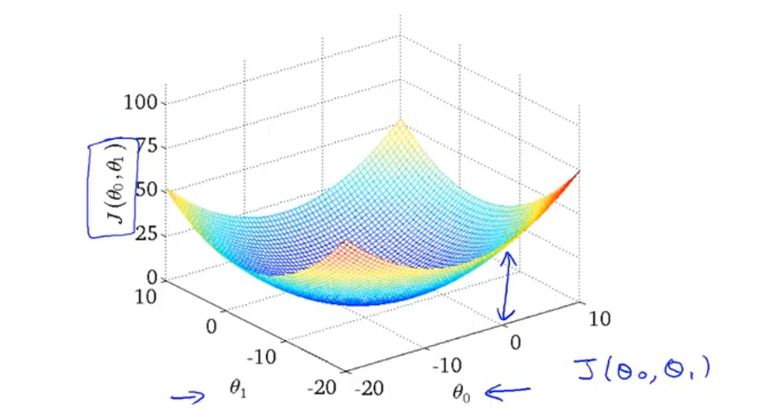
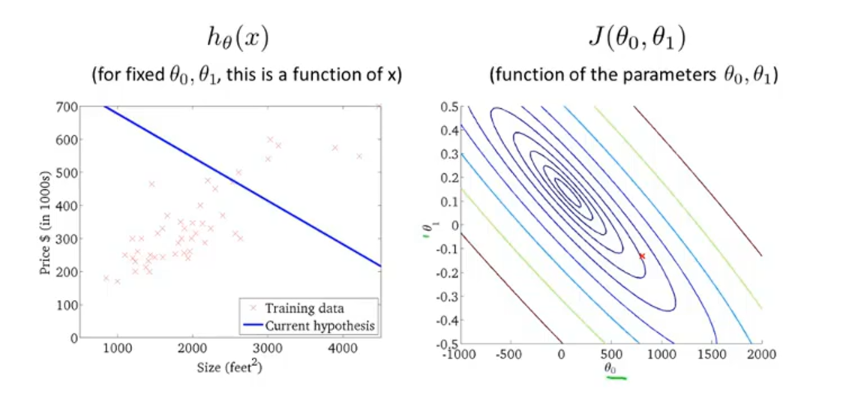
2.3 梯度下降

我们可以通过图像快速观察出代价函数 $J$​ 的最小取值的大致位置，但是我们还是不能很方便地得到代价函数取值最小时 $\theta_0 \theta_1$ 的取值，梯度下降法就是用来将代价函数最小化的常用算法。

2.3.1 算法简单步骤

1. 初始某个起点 $(\theta_0,\theta_1)$
2. 不断一点点改变 $\theta_0,\theta_1$ 去减少 $J$ ，直到达到我们所期望的最小值。

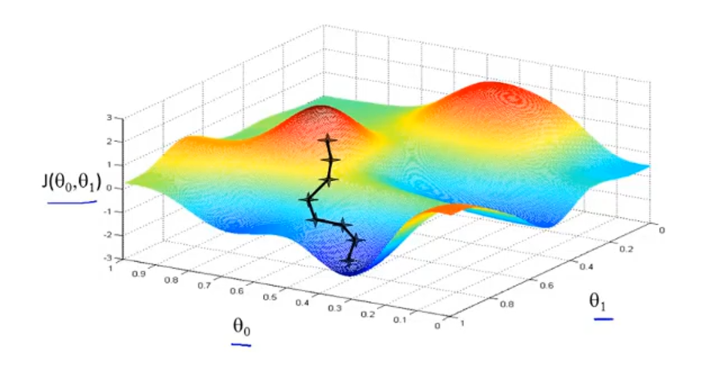
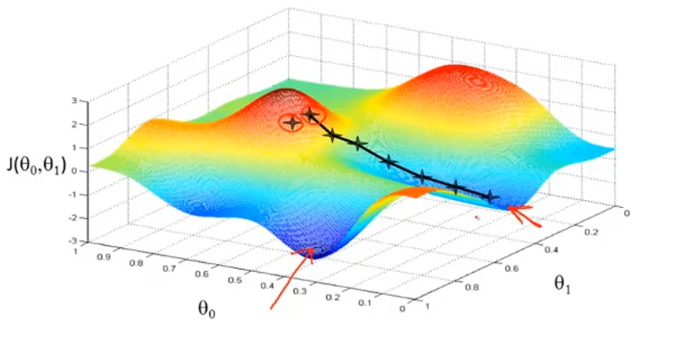
如图所示是某个代价函数的图，将其想象成实际生活中的地形，梯度下降算法的思想是这样的：随机指定一个初始点，假如你要走出很小的一步，并以最快的速度下山，首先环顾四周，然后寻找到坡度最陡的一个方向走，一直重复直到走到最低谷。如果，初始点在右侧一点，你可能会走到另外一个局部最低点，这也是梯度下降的一个特点。

2.3.2 数学表达

不断重复步骤直到收敛：$\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) j \in \{0,1\}$​，其中 $:=$​ 表示赋值操作，$\alpha$​ 称为 学习率，表示每次下山时步子的大小，即梯度下降的速度，需要注意的是，每次更新 $\theta_0\theta_1$​​ 是同时进行的，不能先更新 $\theta_0$​ 然后用更新后的值去更新 $\theta_1$​​。

对于偏导项，可以通过下图理解：同样将三维简化成二维（$\theta_0 = 0$），那么偏导项就是该点的斜率。

• 如果斜率为正数，那么 $\theta_j$ 会变小，即向左移动。
• 如果斜率为正数，那么 $\theta_j$ 会变大，即向右移动。

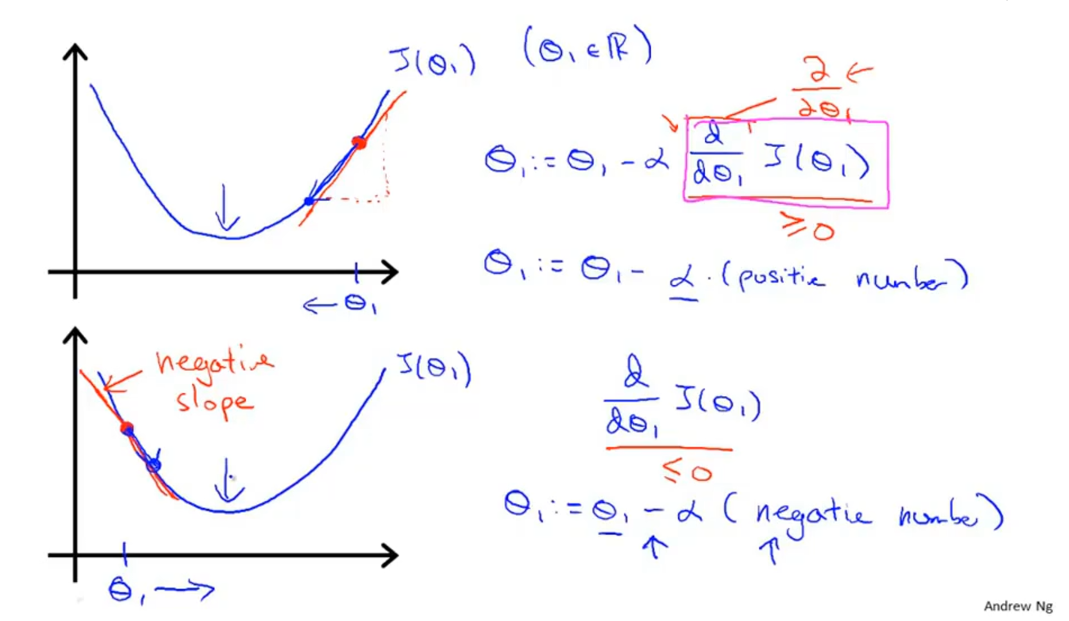
对于 $\alpha$​ 的取值，如果太小会导致效率过低，如果太大会导致收敛失败甚至发散：

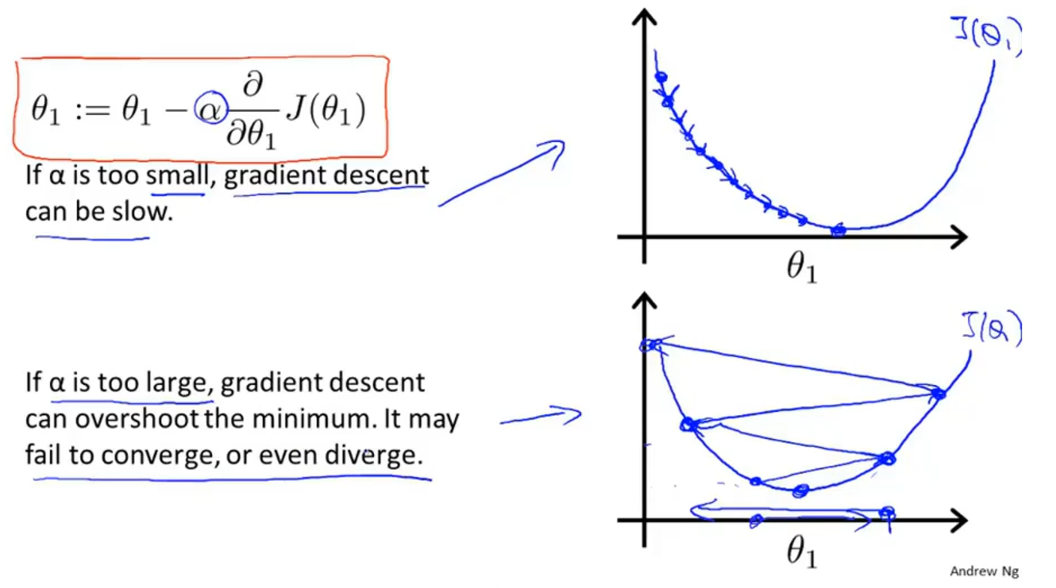
即时 $\alpha$ 为一个常数，在梯度下降的过程中，由于斜率会越来越小最终到达某个局部最优解（斜率为0），所以$\alpha \frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$ 也会越来越小，即每次下降的幅度也会越来越小直到为0。

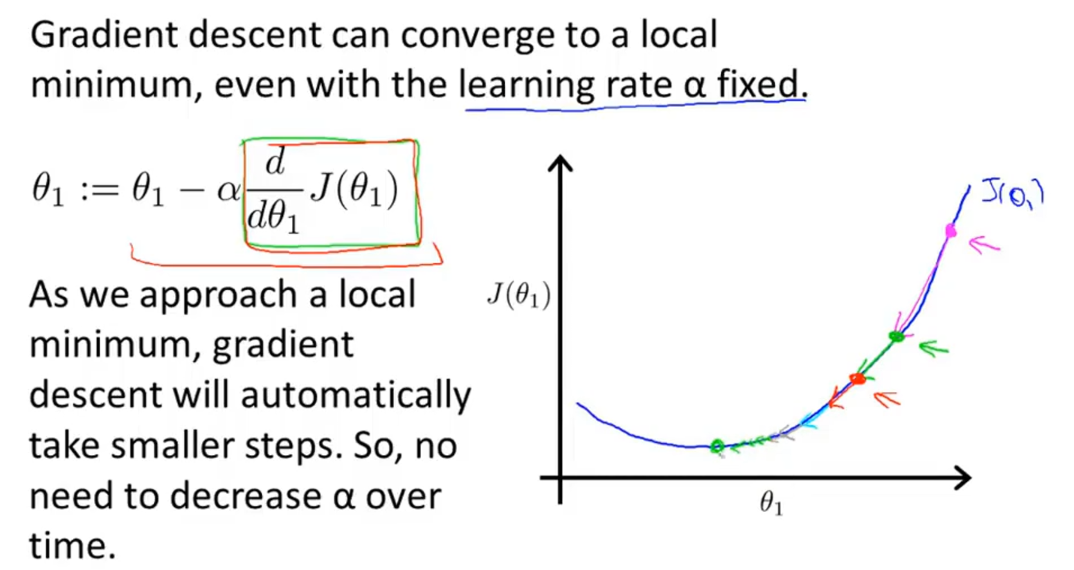
2.3 线性回归算法

线性回归模型：

$h_{\theta}(x) = \theta_0 + \theta_1x$

$J(\theta_0,\theta_1)=\frac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)}) - y^{(i)})^2$

梯度下降算法：

不断重复 $\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) j \in \{0,1\}$​​ 步骤直到收敛。

首先计算一下偏导数部分：

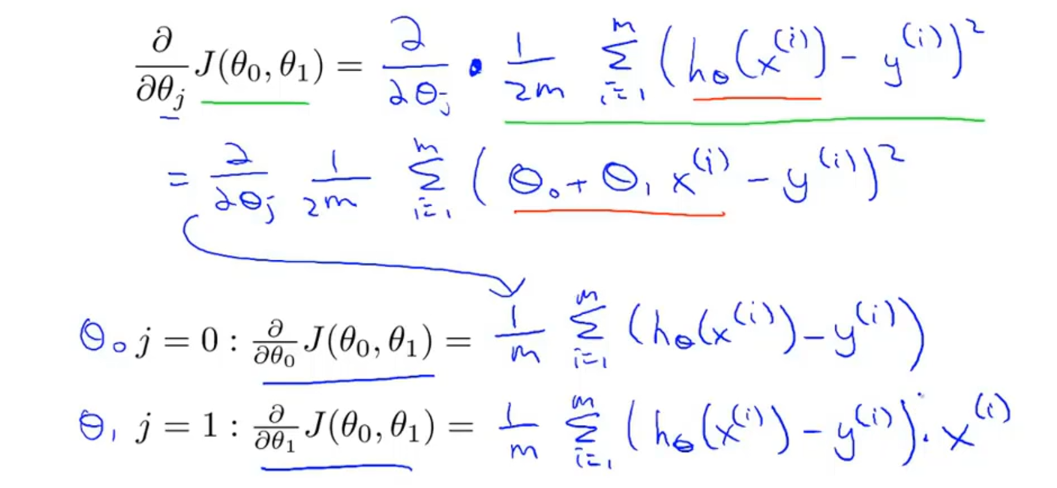
将计算结果代回到梯度下降算法，得到线性回归算法：

不断重复，直到收敛：$\{$

$\theta_0 := \theta_0 - \alpha\frac{1}{m}\displaystyle\sum_{i = 1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})$

$\theta_1 := \theta_1 - \alpha\frac{1}{m}\displaystyle\sum_{i = 1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})x^{(i)}$

$\}$

注意这里的 $x^{(i)}$ 是在累加函数内的

虽然梯度下降算法可能会进入局部最优解，但是线性回归的代价函数是一个凸函数，即只有一个全局最优解，没有局部最优解，所以使用梯度下降法时一定能找到最优的解。

上述算法又称为 batch梯度下降法，因为每次下降都会遍历整个训练集的所有数据。

三、多变量线性回归

3.1 符号定义及向量化

$n$ ：表示一条数据的属性的个数。

$m$ ：表示训练集内数据的条数。

$x^{(i)}$ ：表示训练集内第 i 个数据。

$x^{(i)}_j$ ：表示训练集内第 i 个数据的第 j 个属性的值。

由于代价函数中要对训练集中的每一个数据都进行运算后求和，如果用循环的方式代码会很复杂并且效率低下，所以可以考虑将其转换成矩阵运算，及将数据进行向量化。具体如下：

我们假设： $\theta=\left[\begin{array}{c} \theta_{0} \\ \theta_{1} \\ \cdot \\ \cdot \\ \dot{\theta}_{n} \end{array}\right]$，$X=\left[\begin{array}{ccccc} 1 & x_{1}^{(1)} & x_{2}^{(1)} & \ldots & x_{n}^{(1)} \\ 1 & x_{1}^{(2)} & x_{2}^{(2)} & \ldots & x_{n}^{(2)} \\ \cdot & \cdot & \cdot & \ldots & \cdot \\ \cdot & \cdot & \cdot & \ldots & \cdot \\ \cdot & . & . & \ldots & \cdot \\ 1 & x_{1}^{(m)} & x_{2}^{(m)} & \ldots & x_{n}^{(m)} \end{array}\right]$，$y=\left[\begin{array}{c} y^{(1)} \\ y^{(2)} \\ \cdot \\ y^{(m)} \end{array}\right]$，则：

假设函数：$h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_1x_1 + ... + \theta_nx_n$，等价于矩阵运算：$h_{\theta}(x) = X\theta$ ，其中向量 $\theta$ 也是多变量线性回归的模型参数。同理，代价函数$J(\theta) = \frac{1}{2m}\displaystyle\sum_{i=1}^m(h_{\theta}(x^{(i)}) - y^{(i)})^2$ 就可以表示为 $J(\theta) = \frac{1}{2m}\sum(X\theta-y)^2$。

3.2 多元梯度下降法

类比可以得到，多元梯度下降法的算法表达为：重复进行 $\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta)$ ,直到收敛，即对每个 $\theta_j$ 求偏导，我们可以得到每一步，每个$\theta_j$ 的更新方式，注意要同时更新，求偏导的公式可以推到得到：$\theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$，这里的 $x^{(i)}_j$ 是在累加函数内的。

同样，这里我们也可以进行向量化的操作：

我们设$\delta=\left[\begin{array}{c} \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)} \\ \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{1}^{(i)} \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{n}^{(i)} \end{array}\right]=\frac{1}{m}\left[\begin{array}{cccccc} 1 & 1 & \cdot & \cdot & \cdot & 1 \\ x_{1}^{(1)} & x_{1}^{(2)} & \cdot & \cdot & \cdot & x_{1}^{(m)} \\ x_{2}^{(1)} & x_{2}^{(2)} & \cdot & \cdot & \cdot & x_{2}^{(m)} \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot& \cdot & \cdot & \cdot & \cdot & \cdot \\ x_{n}^{(1)} & x_{n}^{(2)} & \cdot & \cdot & \cdot & x_{n}^{(m)} \end{array}\right] \cdot(X \cdot \theta-y)=\frac{1}{m} X^{T} \cdot(X \cdot \theta-y)$，$\theta=\left[\begin{array}{c} \theta_{0} \\ \theta_{1} \\ \cdot \\ \cdot \\ \dot{\theta}_{n} \end{array}\right]$ ，那么

$\theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$ 就可以写成 $\theta = \theta - \alpha\delta$， 所以 $\theta=\theta-\alpha \frac{1}{m} X^{T}(X \theta-y)$

一点解释：

刚开始接触的时候很难理解这是怎么推得的（可能是我线代太差了），想了好久，在原理上大概理解了，首先提取出 $\frac{1}{m}$ 没什么好说的。然后先看$X\theta - y$ 这里得到的是一个 m * 1 的列向量，每一行表示的是第 $i$ 个数据计算得到的 $h_{\theta}(x^{(i)}) - y^{(i)}$ ，然后左边的一大坨矩阵是一个 n * m 的矩阵，进行矩阵相乘，发现就是相等的，虽然不知道是怎么想到这样的变换过程的，可能有什么定理，但是还算是理解了，留个坑，以后如果懂了再填原理的坑吧！

3.3 特征缩放

3.3.1 主要思路

思路：设法将特征的取值维持在一个相近的范围。

比如有两个属性，房屋大小（取值为0-2000），卧室个数（取值1-5），那么如果画出等高线图，会是一个又高又瘦的形状，如果用梯度下降算法，会收缩地非常缓慢（如下图左）。我们可以将房屋大小除以2000，将卧室个数除以5，再画出等高线图就比较合适了（如下图右）。

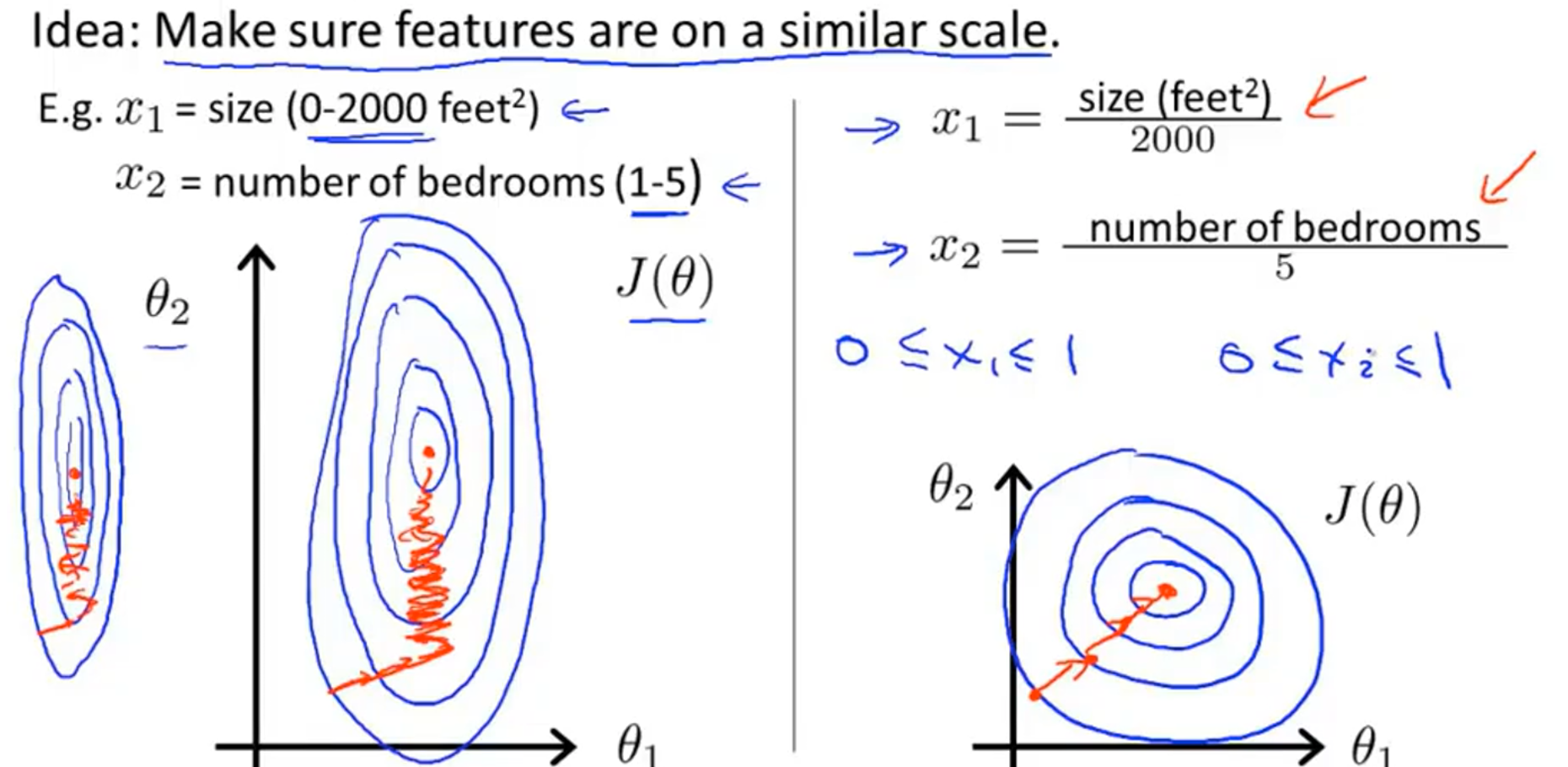
更一般地来说：就是要讲每个属性的取值范围都缩放到接近 $[-1,1]$ 之间。注意： 如果取值范围过大或过小都是不能接受的，但是如果取值范围接近就可以结束，比如$[-2,3]$ 可以接受，但是 $[-300,400]$ 和 $[-0.0001,0.0001]$ 这种取值范围是不能接受的。

3.3.2 均值归一化

对于一个属性，求出该属性所有样本的平均值，再将每个样本的该属性值减去平均值，使得这个属性所有样本的平均值变为0，然后再除以这个属性原始的取值范围（最大值-最小值）。如：若房屋面积的取值范围为 $[0,2000]$，有一个训练集，房屋面积的平均值为1000，则将每条数据的房屋面积属性组-1000，然后再除2000。

数学表达：$x_i := \frac{x_i-\mu_i}{s_i}$,其中 $\mu_i$ 表示数据集中 $x_i$ 的平均值，$s_i$ 指的是取值范围，即最大值-最小值。

3.4 学习率的选取

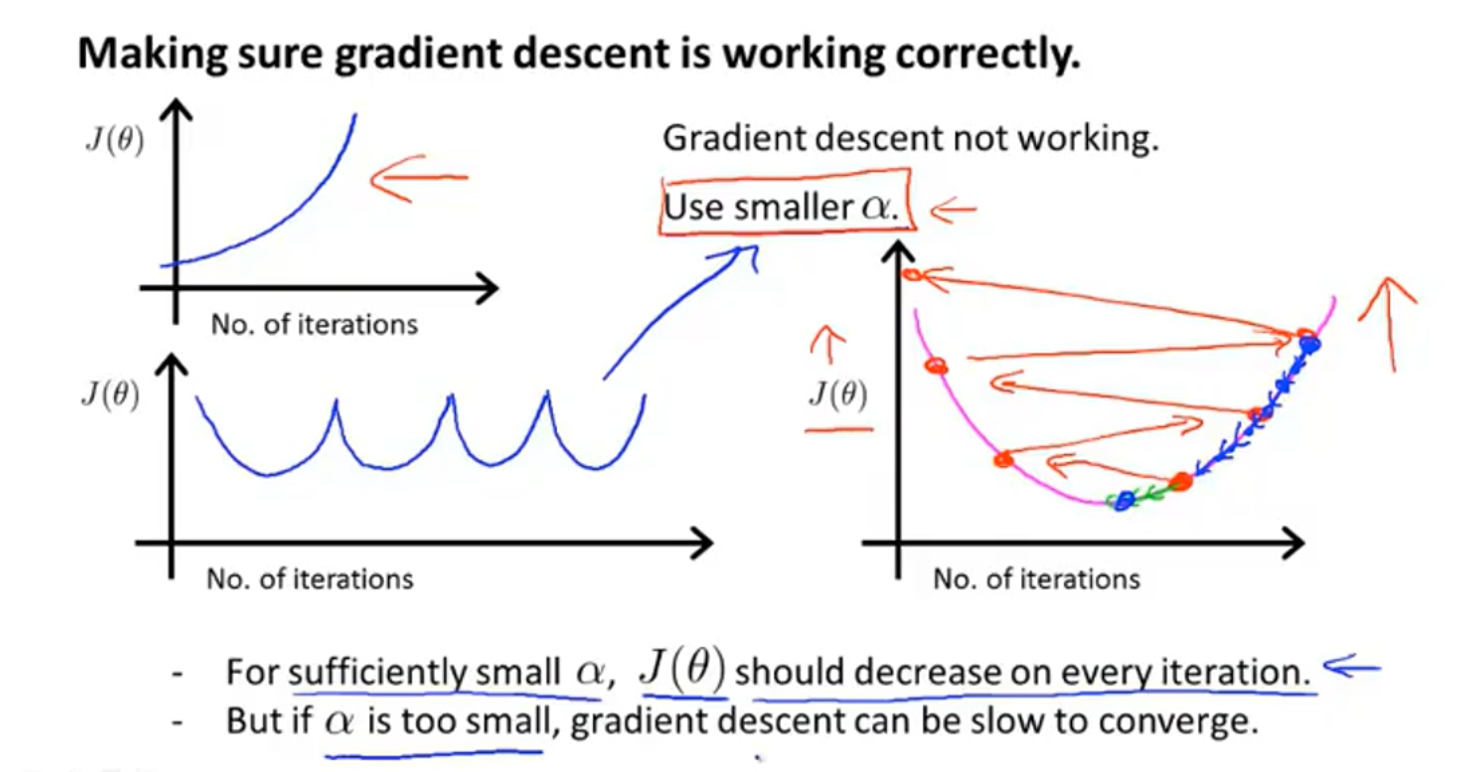
如果代价函数关于迭代次数的图形形如左上角这两张一样，说明学习率 $\alpha$ 取值过大，在线性回归模型中，数学证明得到，只要$\alpha$ 足够小，每次迭代代价函数都是一定会下降的，当然需要注意的是，如果$\alpha$ 过小，会导致梯度下降非常缓慢。

3.5 特征选择和多项式回归

以房价预测为例，如果有两个属性分别表示房屋的长和宽，可以将两个属性相乘得到一个新的属性：面积，用面积属性来预测房价显然更加合适。选择好特征后，考虑用什么多项式模型进行拟合。

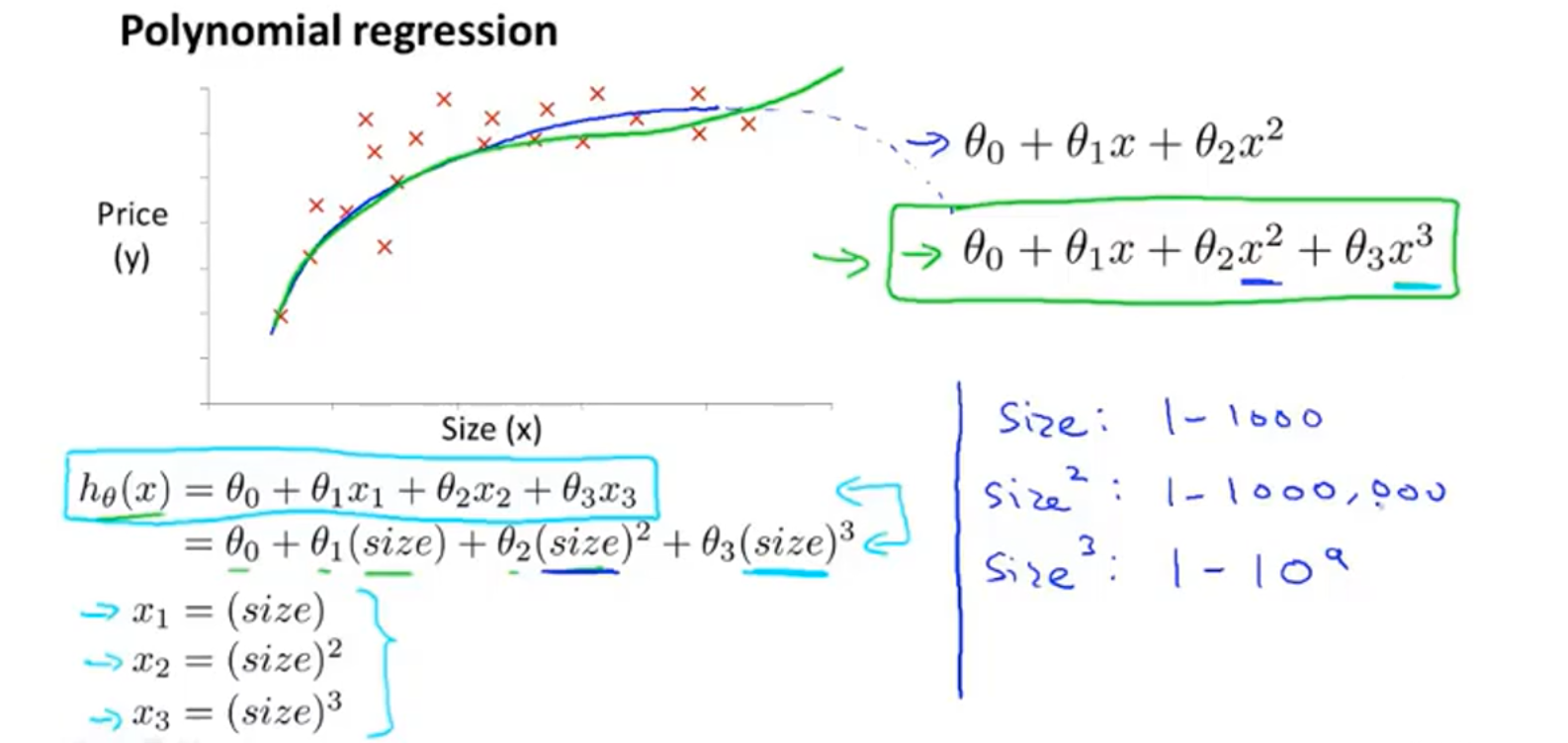
如果使用一个二次函数来拟合，函数图形会先上升后下降，显然不太符合实际，考虑用三次函数进行拟合，那么三个属性分别就是面积、面积的平方、面积的三次方。由于三个属性的取值范围相差很大，所以需要用到特征缩放的思想。当然，还有许多其他模型可以选取，选择合适的函数进行拟合，很重要，后面会学习算法来决定选择哪些特征，用什么模型进行拟合。

3.6 正规方程

3.6.1 工作方式

不同于梯度下降法不断迭代的方法，正规方程提供了一种直接计算模型参数 $\theta$ 的方法。

先给出求法：$\theta = (X^TX)^{-1}X^Ty$。

• 构建 $X$ 矩阵和 $y$ 矩阵：

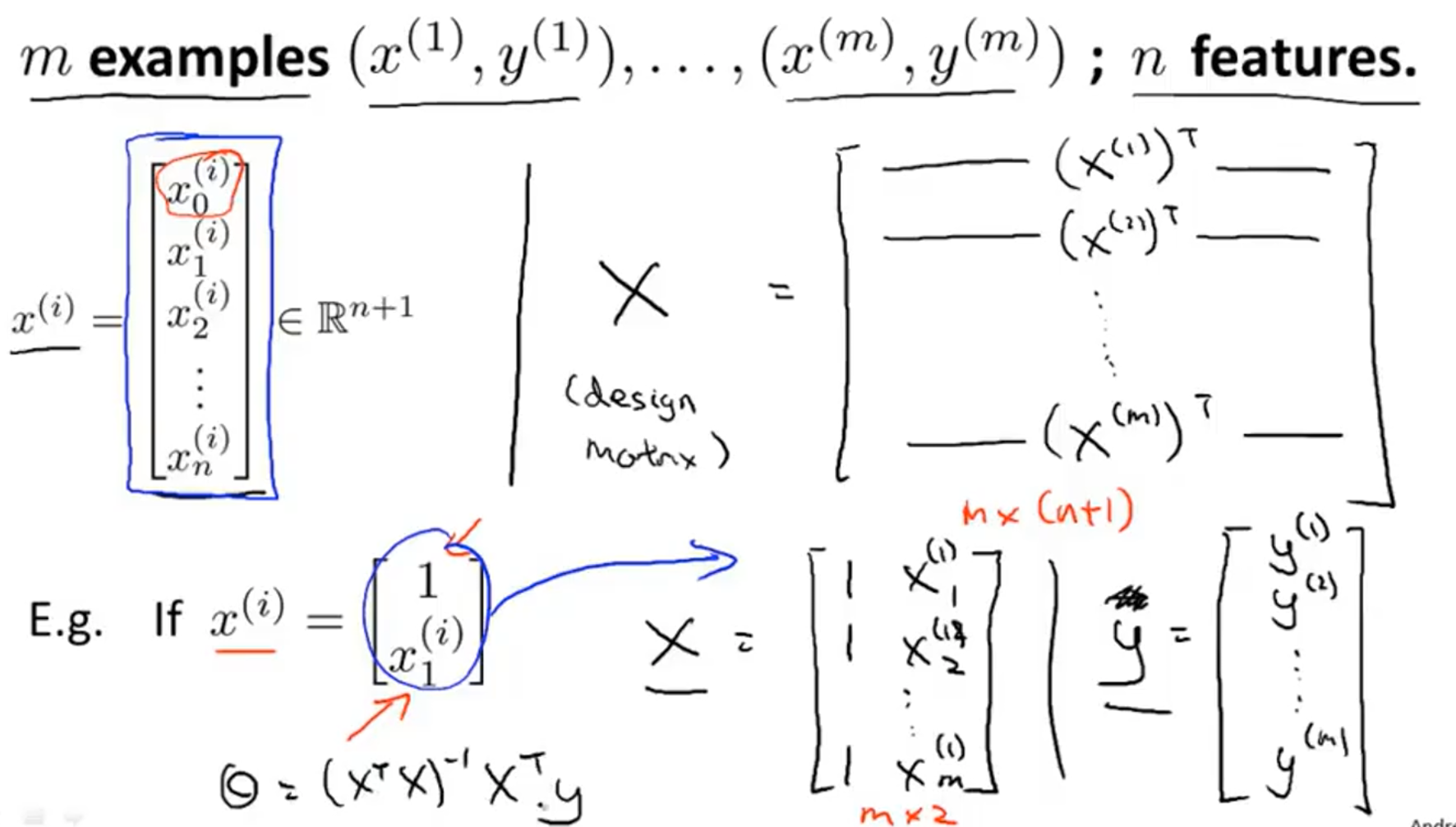
假设有m个样例，n个属性，$X$矩阵就行将每个样例横着依次放置， $y$ 矩阵就是将答案竖着依次放置。

• $\theta = (X^TX)^{-1}X^Ty$

$X^T$ 表示倒置，$(X^TX)^{-1}$ 表示求其逆，数学上可以证明，这就是最优解，且用这种方法计算时无需用到特征缩放。

在matlab中，可以用代码 pinv(x'*x)*x'*y 来计算上述方程。

3.6.2 与梯度下降的区别

简单来说，小数据用正规方程，大数据用梯度下降。

3.7 正规方程在矩阵不可逆情况下的解决方法

虽然可能会出现矩阵不可逆的情况，但是pinv(x'*x)*x'*y 在MATLAB 中保证可以求得正解，这是函数实现上的一些问题。

如果矩阵不可以一般有两种可能原因：

• 学习时，包含多余特征，如：

  同时有两个特征：一个是以平方英尺为单位的房屋面积，一个是以平方米为单位的房屋面积，由于两者可以相互线性表示，所以会导致矩阵不可逆的情况。

• 学习时，包含过多的特征（具体来说就是 $m\le n$）,此时可以选择删去一些特征，或者使用正则化（后面会提到）。