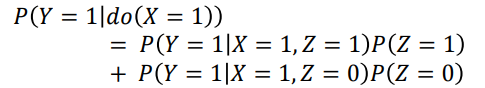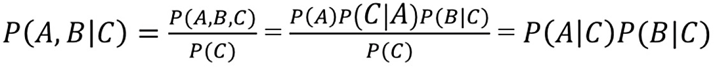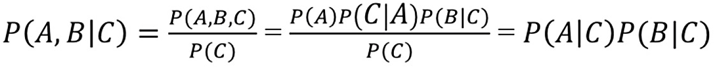一、命题逻辑

1.1 命题逻辑的定义

• 命题逻辑(proposition logic)是应用一套形式化规则对以符号表示的描述性陈述进行推理的系统。

• 在命题逻辑中，一个或真或假的描述性陈述被称为原子命题，对原子命题的内部结构不做任何解析。

• 若干原子命题可通过逻辑运算符来构成复合命题。

如：

p: 北京是中国的首都

r : x<8

p为真命题，q为假命题，r不是命题，因为无法判断真假。

1.2 命题联结词

五个联结词：

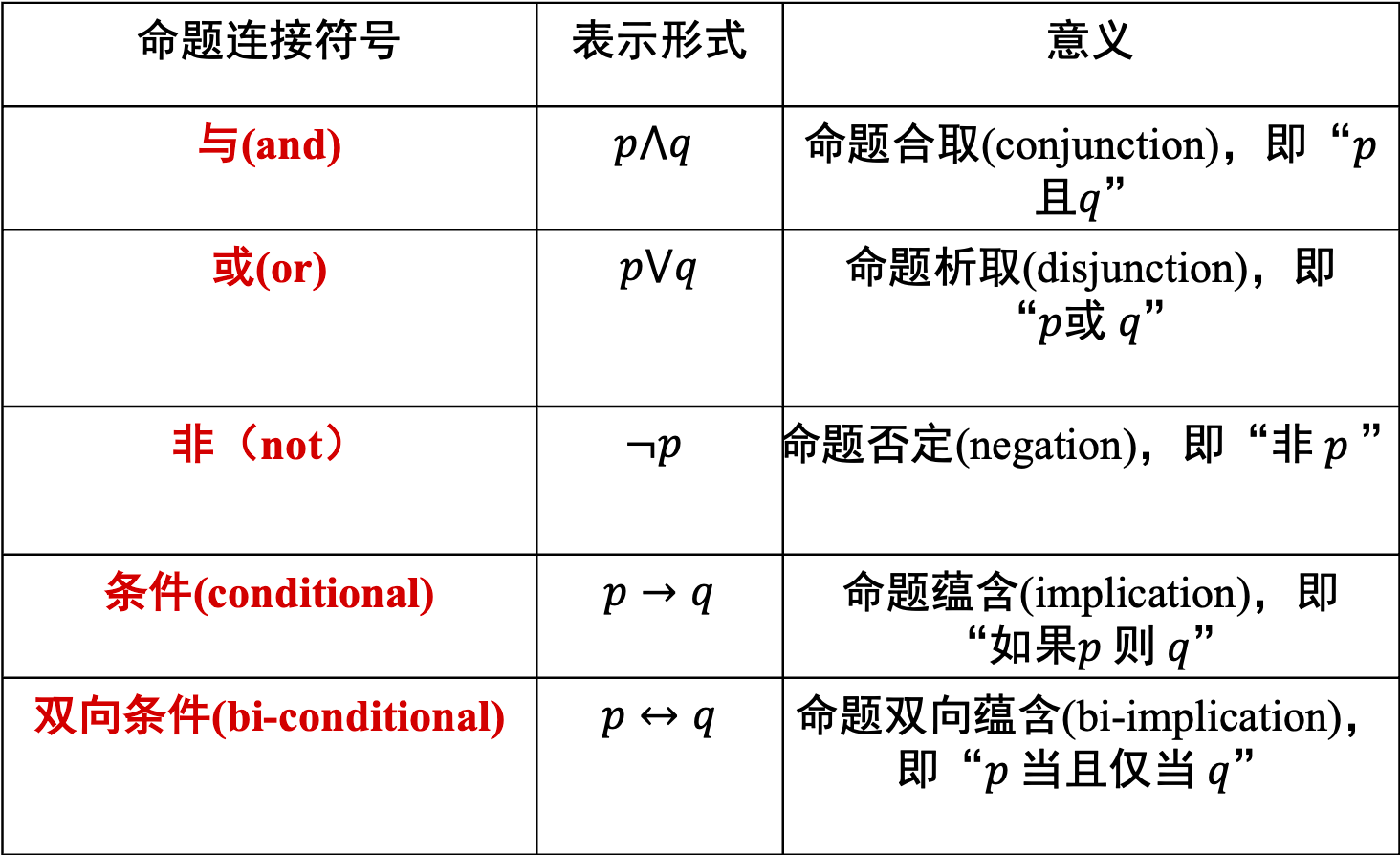
联结词的真值表：

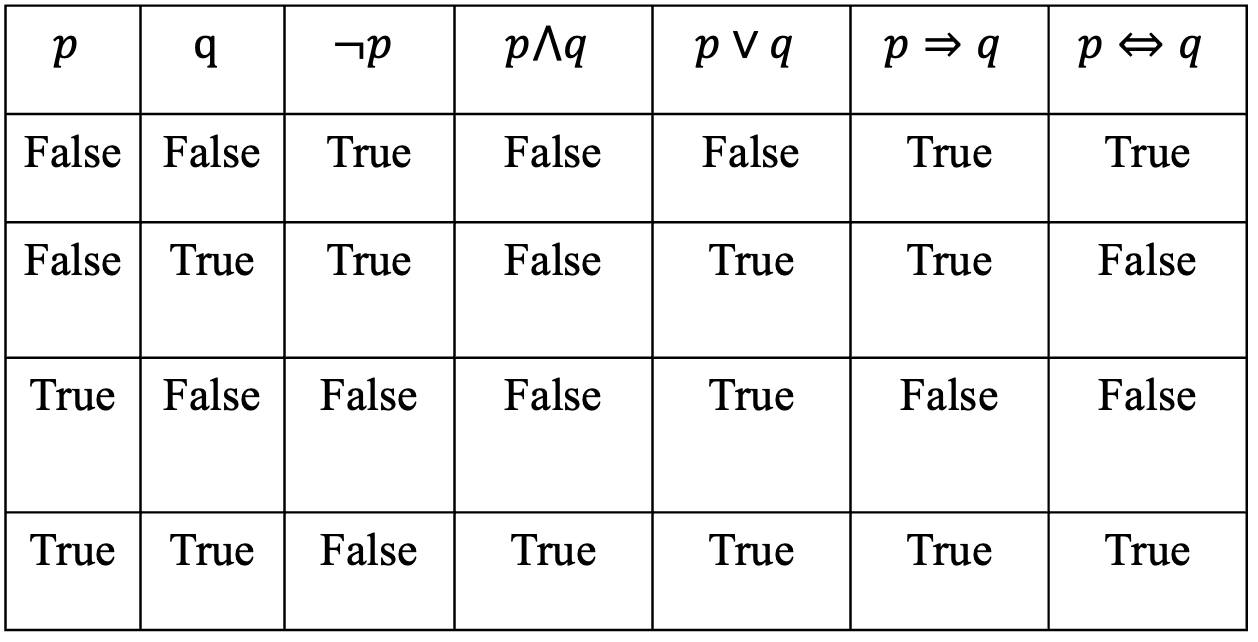
对于条件和双向条件两个联结词：

“如果p那么q(p⟶q)”定义的是一种蕴涵关系（即充分条件），也就是命题q 包含着命题p （ p是q的子集）。p不成立相当于p是一个空集，空集可被其他所有集合所包含，因此当p不成立时，“如果p那么q”永远为真，真值表对于为 True。

1.3 逻辑等价

定义：给定命题p和命题q，如果p和q在所有情况下都具有同样真假结果，那么p和q在逻辑上等价，一般用≡来表示，即p≡q。

1.4 推理规则

1.5 命题范式

• 有限个简单合取式构成的析取式称为析取范式

• 有限个简单析取式构成的合取式称为合取范式

• 析取范式和合取范式统称为范式（normal form）

性质：

• 一个析取范式是不成立的，当且仅当它的每个简单合取式都不成立。

• 一个合取范式是成立的，当且仅当它的每个简单析取式都是成立的。

• 任一命题公式都存在着与之等值的析取范式与合取范式（注意：命题公式的析取范式与合取范式不是唯一的）

二、谓词逻辑

2.1 定义

命题逻辑的局限性：在命题逻辑中，每个陈述句是最基本的单位(即原子命题)，无法对原子命题进行分解。因此在命题逻辑中，不能表达局部与整体、一般与个别的关系。

在谓词逻辑中，将原子命题进一步细化，分解出个体、谓词和量词，来表达个体与总体的内在联系和数量关系，这就是谓词逻辑研究内容。其中，个体、谓词（predicate）和量词（quantifier）为三个核心概念。

• 个体：所研究领域中可以独立存在的具体或抽象的概念。
• 谓词：用来刻画个体属性，或者个体间关系的存在性的元素，值为真或假，有几个参数就是几元谓词。
• 全称量词：全称量词用符号∀表示，表示一切的、凡是的、所有的、每一个等。 ∀x表示定义域中的所有个体， (∀x)P(x)表示定义域中的所有个体具有性质P
• 存在量词：存在量词用符号∃表示，表示存在、有一个、某些等。 ∃x表示定义域中存在一个或若干个个体，(∃x)P(x)表示定义域中存在一个个体或若干个体具有性质P

2.2 全称量词与存在量词之间的组合

• $(∀x)¬P(x)≡(¬∃x)P(x) $

• $(¬∀x)P(x)≡(∃x)¬P(x)$

• $(∀x)P(x)≡(¬∃x)¬P(x)$

• $(∃x)P(x)≡ (¬∀x)¬P(x)$

2.3 合式公式：

• 命题常项、命题变项、原子谓词（不存在任何量词与联结词）是合式公式。

• 如果A和B是合式公式，那么¬A、 A∧B、 A∨B、 A→B 、 A⟷B 都是合式公式

• 如果A是合式公式， x是个体变元，则∃xA(x) 和∀xA(x)也是合式公式

• 有限次地使用上述规则求得公式是合式公式

2.4 推理规则：

全称量词消去(Universal Instantiation, UI): $(∀x)A(x)→A(y)$

全称量词引入(Universal Generalization, UG): $A(y)→(∀x)A(x)$

存在量词消去(Existential Instantiation, EI): $(∃x)A(x)→A(c)$

存在量词引入(Existential Generalization, EG): $A(c)→(∃x)A(x)$

2.5 自然语言的形式化：

前提：1) 每驾飞机或者停在地面或者飞在天空；2) 并非每驾飞机都飞在天空

结论：有些飞机停在地面

形式化：plane(x): x是飞机；in_ground(x): x停在地面；on_fly(x): x飞在天空

已知：$$(∀x)(plane(x)→in_ground(x)∨on_fly(x)), (¬∀x)(plane(x)→on_fly(x))$$

请证明：$$(∃x)(plane(x)∧in_ground(x))$$

三、知识图谱推理

3.1概念

3.1.1 知识图谱的定义

知识图谱可视为包含多种关系的图。在图中，每个节点是一个实体（如人名、地名、事件和活动等），任意两个节点之间的边表示这两个节点之间存在的关系。一般而言，可将知识图谱中任意两个相连节点及其连接边表示成一个三元组（triplet）, 即 (left_node, relation, right_node) ，例：(水利工程, is an, 工程)。下图所示的知识图谱中，已知三峡大坝和葛洲坝为水利工程且位于同一流域，两者之间具有反调节的关系，于是知识图谱通过推理规则可以得知，同属于哥伦比亚河的达拉斯水坝和大古力水坝也具有反调节的关系。这种通过机器学习等方式对知识图谱所蕴含的关系进行挖掘的方法称为知识图谱推理。

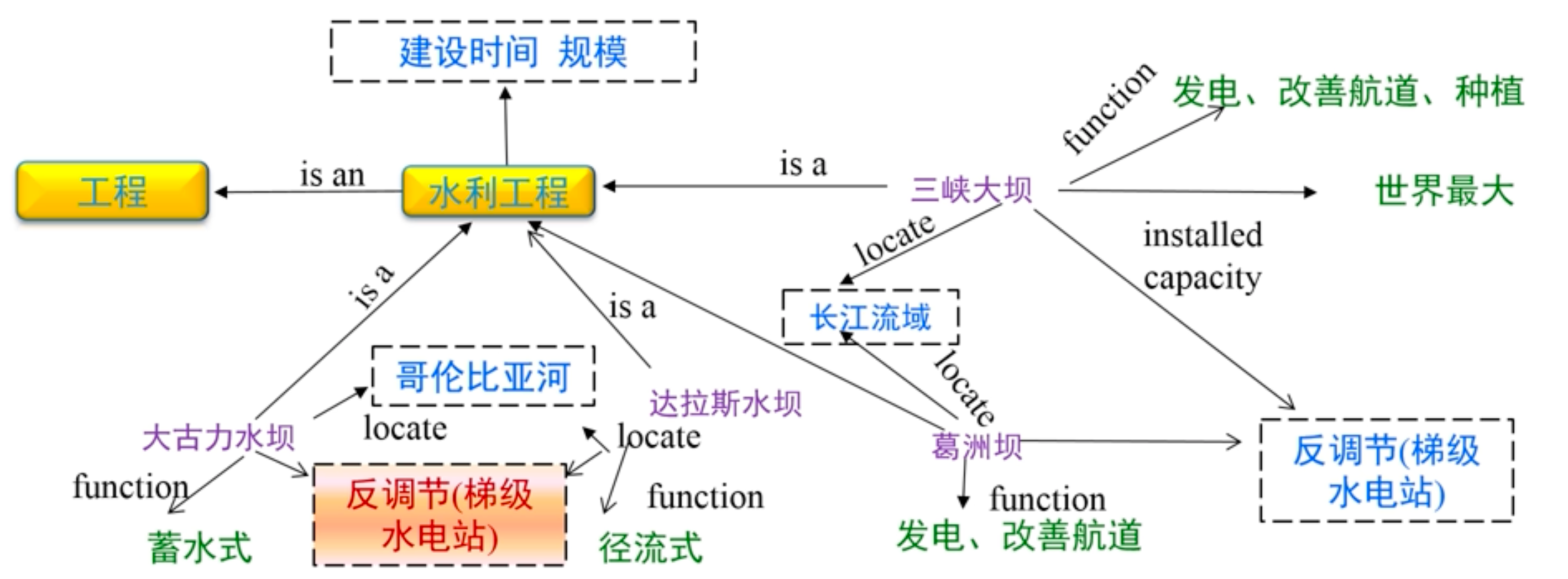
3.1.2 构成

概念：层次化组织

实体：概念的示例化描述

属性：对概念或实体的描述信息

关系：概念或实体之间的关联

推理规则：可产生语义网络中上述新的元素

在实际中，知识图谱一般可以通过标注多关系图（labeled multi-relational graph）来表示，如下图就是一个知识图谱。

3.2 归纳学习

归纳逻辑程序设计 (inductive logic programming，ILP)算法，是机器学习和逻辑程序设计交叉领域的研究内容。ILP使用一阶谓词逻辑进行知识表示，通过修改和扩充逻辑表达式对现有知识归纳，完成推理任务。作为ILP的代表性方法，FOIL（First Order Inductive Learner）通过序贯覆盖实现规则推理。

可利用一阶谓词来表达刻画知识图谱中节点之间存在的关系，如图中形如<James,Couple,David>的关系可用一阶逻辑的形式来描述，即Couple(James, David)。

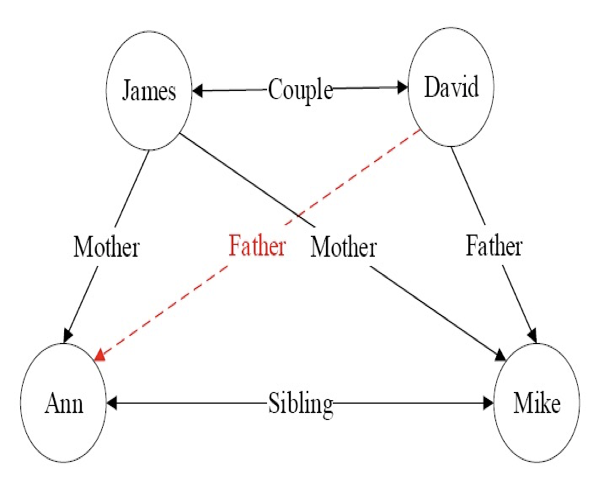
Couple(x, y)是一阶谓词，Couple是图中实体之间具有的关系，x和y是谓词变量

从图中已有关系可推知David和Ann具有父女关系，但这一关系在图中初始图(无红线)中并不存在，是需要推理的目标。用数学语言描述父女的关系就是：$(∀x)(∀y)(∀z)(Mother(z, y)∧ Couple(x,z)→Father(x, y))$，那么如何通过归纳学习推理得到这条规则呢？

下面用FOIL来进行推理：

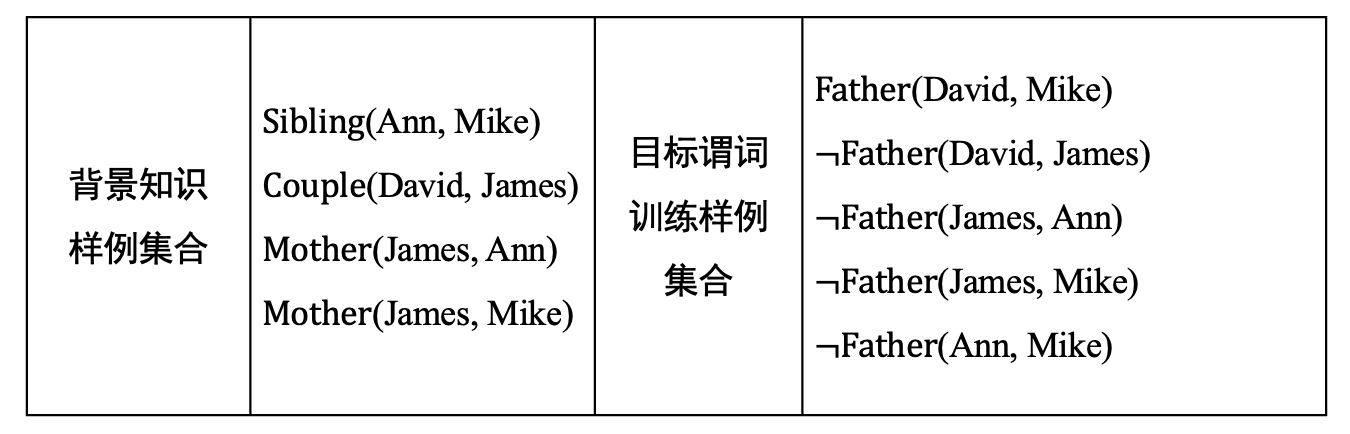
FOIL算法推理手段：正例+反例+背景知识=>目标谓词

3.2.1 一些概念

目标谓词：Father(x, y)，此例中目标谓词只有一个正例Father(David, Mike)。

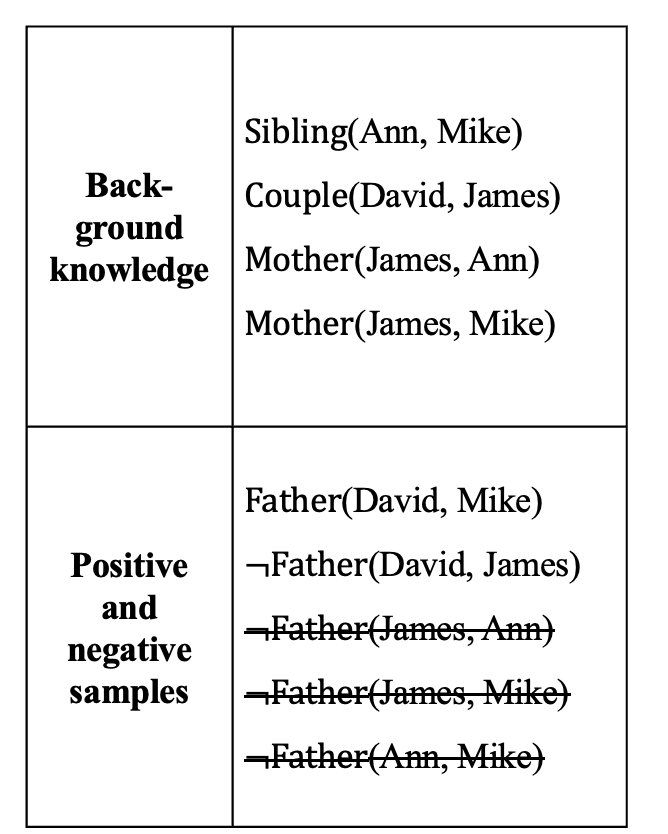
反例在知识图谱中一般不会显式给出，但可从知识图谱中构造出来。如从知识图谱中已经知道Couple(David, James)成立，则Father(David, James)可作为目标谓词P的一个反例，记为¬Father (David, James)。只能在已知两个实体的关系且确定其关系与目标谓词相悖时，才能将这两个实体用于构建目标谓词的反例，而不能在不知两个实体是否满足目标谓词前提下将它们来构造目标谓词的反例。

背景知识：知识图谱中目标谓词以外的其他谓词实例化结果，如Sibling(Ann, Mike)。

推理思路：从一般到特殊，逐步给目标谓词添加前提约束谓词，直到所构成的推理规则不覆盖任何反例。

从一般到特殊：对目标谓词或前提约束谓词中的变量赋予具体值，如将$(∀x)(∀y)(∀z)(Mother(z, y)∧ Couple(x,z)→Father(x, y))$这一推理规则所包含的目标谓词Father(x, y)中x和y分别赋值为David和Ann，进而进行推理。

FOIL中信息增益值(information gain)：评判一个前提约束谓词引入的价值，计算公式为：

3.2.2 具体流程

• 首先找出待加入的前提约束谓词和目标样例集合。
  

• 然后依次将谓词加入到推理规则中作为前提约束谓词，并计算所得到新推理规则的FOIL增益值。基于计算所得FOIL增益值来选择最佳前提约束谓词。可以得到下面的计算结果，找到最优的（FOIL增益最大的）加入。

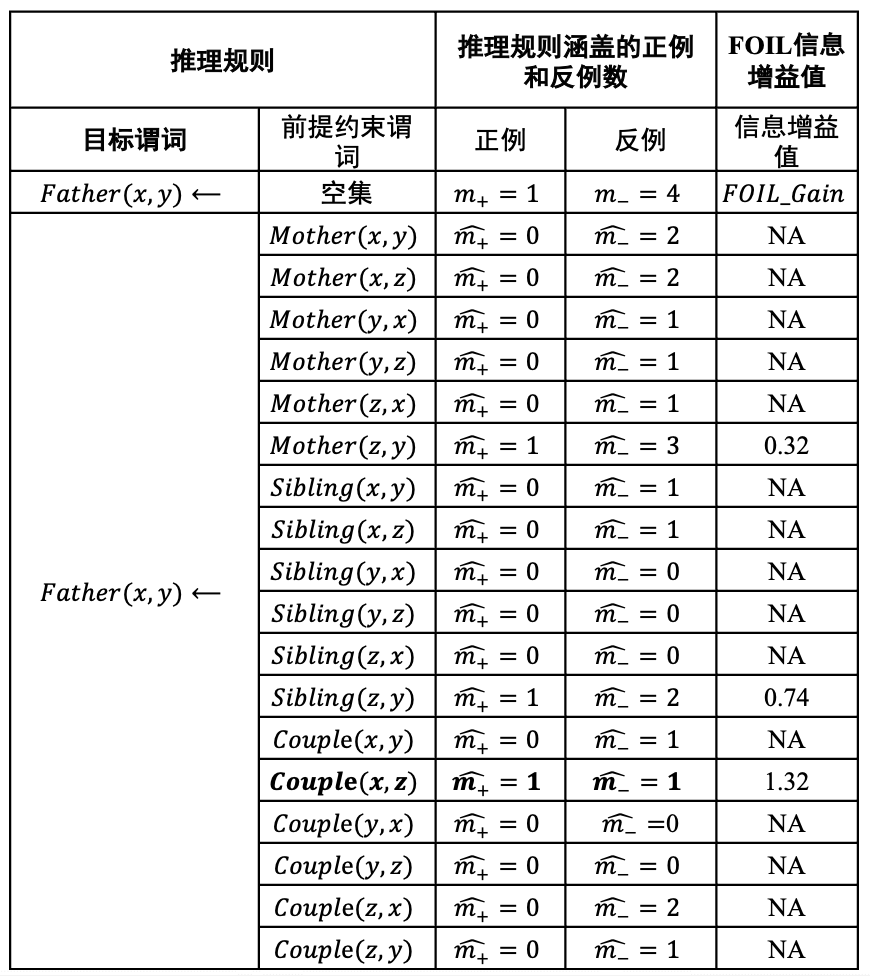
例如将Mother(x, y)作为前提约束谓词加入，可得到推理规则Mother(x, y)→Father(x, y)，在背景知识中，Mother(x, y)有两个实例Mother(James, Ann)和Mother(James, Mike)。对于Mother(James, Mike)这一实例， x= James，y = Mike，将x和y代入Father(x, y)得到Father(James, Mike)，可知在训练样本中Father(James, Mike)是一个反例。覆盖正例和反例数量分别为0和2，算出收益以为负无穷，记为NA，依次计算，发现是最优的前提约束谓词。

• 将Couple(x,z)加入到推理规则，得到Couple(x,z)→Father(x, y)新推理规则将训练样例中与该推理规则不符的样例去掉。这里不符指当Couple(x,z)中x取值为David时，与Father(David, )或¬Father(David, )无法匹配的实例。训练样本集中只有正例Father(David, Mike)和负例¬Father(David, James)两个实例。

• 继续计算信息增益量，发现mother(z,y) 最大，将Mother(z, y)加入，得到新推理规则$Mother(z, y)∧ Couple(x,z)→Father(x, y)$

  当x=David、y=Mike、z=James时，该推理规则覆盖训练样本集合中正例Father(David, Mike)且不覆盖任意反例，因此算法学习结束。

• 总结：给定目标谓词，FOIL算法从实例（正例、反例、背景样例）出发，不断测试所得到推理规则是否还包含反例，一旦不包含负例，则学习结束，展示了 “归纳学习”能力。

3.3 路径排序

与FOIL算法不同，路径排序推理算法（PRA）的基本思想是将实体之间的关联路径作为特征，来学习目标关系的分类器。

路径排序算法的工作流程主要分为三步：

(1) 特征抽取：生成并选择路径特征集合。生成路径的方式有随机游走（random walk）、广度优先搜索、深度优先搜索等。

(2) 特征计算：计算每个训练样例的特征值$P(s \rightarrow t;\pi_j)$​。该特征值可以表示从实体节点s出发，通过关系路径$\pi_j$​到达实体节点t的概率；也可以表示为布尔值，表示实体s到实体t之间是否存在路径$π_j$；还可以是实体s和实体t之间路径出现频次、频率等。

(3) 分类器训练：根据训练样例的特征值，为目标关系训练分类器。当训练好分类器后，即可将该分类器用于推理两个实体之间是否存在目标关系。

四、因果推理

4.1 因果推理概述

4.1.1 辛普森悖论

定义：辛普森悖论表明，在某些情况下，忽略潜在的“第三个变量”，可能会改变已有的结论，而我们常常却一无所知。从观测结果中寻找引发结果的原因、考虑数据生成的过程，由果溯因，就是因果推理。

4.1.2 因果推理主要模型：

• 结构因果模型(structural causal model, SCM)：也被称为因果模型（causal model）或Neyman–Rubin因果模型。
• 因果图（causal diagram）：Judea Pearl 1995年提出。每个结构因果模型M都与一个因果图G相对应。
• 关系：每个结构因果模型M都对应一个因果图G相对应

4.1.3 因果推理的层级：

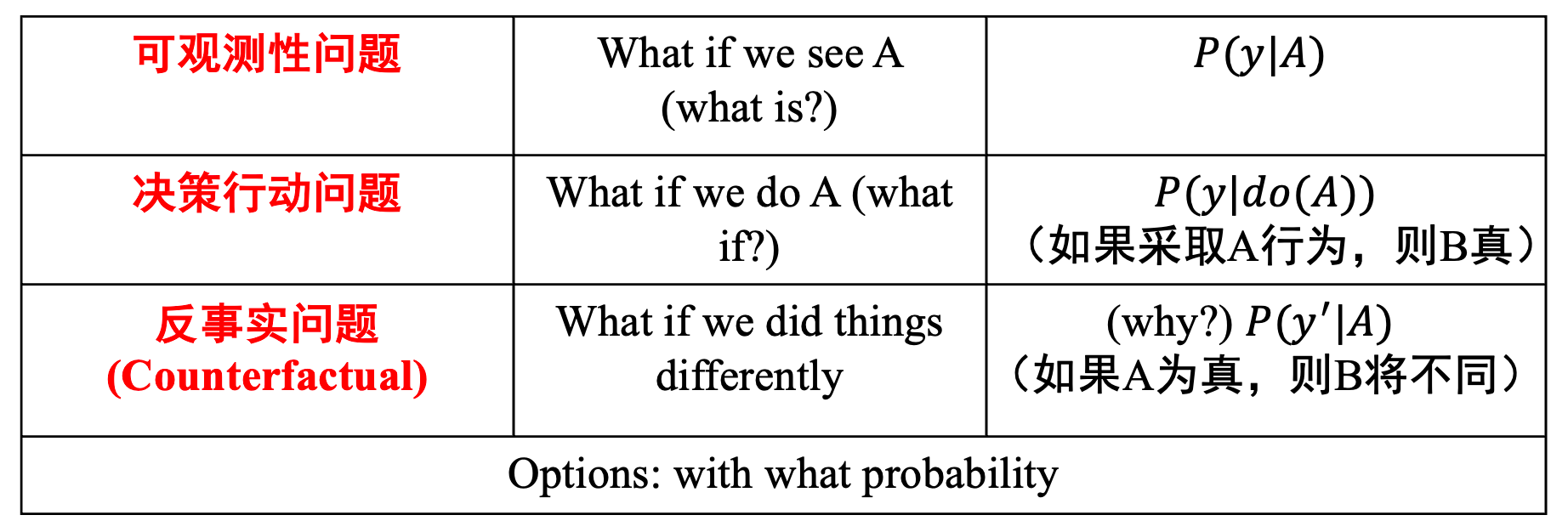
4.1.4 有向无环图

定义：

一般而言，因果图是有向无环图(directed acyclic graphs, DAG)。有向无环图刻画了图中所有节点之间的依赖关系。DAG 可用于描述数据的生成机制。这样描述变量联合分布或者数据生成机制的模型，被称为 “贝叶斯网络”（Bayesian network）。对于任意的有向无环图模型，模型中d个变量的联合概率分布由每个节点与其父节点之间的条件概率 $P(child|parents)$​的乘积给出：

$P(x_1,x_2,…,x_d) = \displaystyle\prod^d_{j = 1}P(x_j|x_{pa(j)})$​，$x_{pa(j)}$ 表示节点$x_j$的父节点集合。

DAG可被视为因果过程：父辈节点“促成”了孩子几点的取值，如下图的联合分布例子：

可知，一个有向无环图唯一地决定了一个联合分布；反过来，一个联合分布不能唯一的决定有向无环图。反过来的结论不成立。

4.1.5 D-分离

D-分离用于判断集合A中变量是否与集合B中变量相互独立（给定集合C），记为

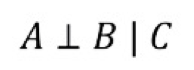
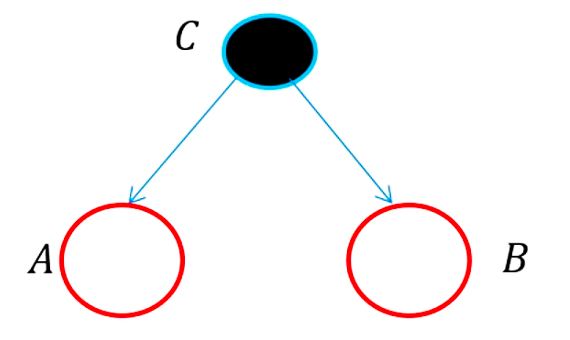
• 例1：
  

  当C取值固定（可观测，observed），有

  

  可见A和B在C取值固定情况下，是条件独立的(即A如何改变不会影响B，因为被C隔断)。

• 例2：

  

  当C取值固定（可观测，observed），有

  

  可见A和B在C取值固定情况下，是条件独立的。

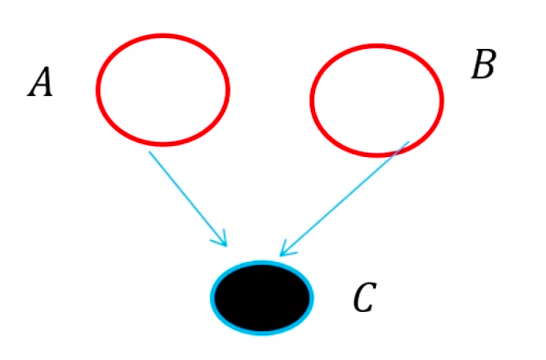
• 例3：

  
  

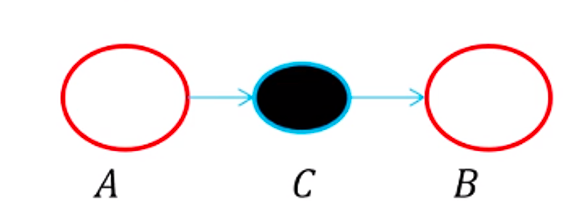
D-分离：对于一个DAG图，如果A、B、C是三个集合（可以是单独的节点或者是节点的集合），为了判断A和B是否是C条件独立的，在DAG图中考虑所有A和B之间的路径（不管方向）。对于其中的一条路径，如果满足以下两个条件中的任意一条，则称这条路径是阻塞（block）的：

D-分离(directional separation, d-separation)方法可用于判断因果图上任意变量间相关性和 独立性。

在因果图上，若两个节点间存在一条路径将这两个节点连通，则称之为是有向连接(dconnected)的；若两个节点不是有向连接的，则称之为是有向分离(d-separated)的，即不 存在这样的路径将这两个节点连通。当两个节点是有向分离时，意味着这两个节点相 互独立。

4.1.6 干预(intervention)和𝒅𝒐 算子(do-calculus)

干预(intervention)指的是固定(fix)系统中某个变量，然后改变系统，观察其他变量的变化。为了与𝑋自然取值𝑥时进行区分，在对X进行干预时，引入“𝒅𝒐算子”，记 作$𝑑𝑜(𝑋 = 𝑥)$。因此，$𝑃(𝑌 = 𝑦|𝑋 = 𝑥)$​表示当 𝑋 取值为 𝑥 时，$𝑌 = 𝑦$ 的概率； 而$𝑃(𝑌 = 𝑦|𝑑𝑜(𝑋 = 𝑥))$ 表示对𝑋取值进行了干预，固定其取值为 𝑥 时，𝑌 = 𝑦 的概率。用统计学的术语来说，$𝑃(𝑌 = 𝑦|𝑋 = 𝑥)$​反映了在取值为 𝑥 的个体 𝑋 上，𝑌的总体分布；而𝑃(𝑌 = 𝑦|𝑑𝑜(𝑋 = 𝑥))反映的是如果将 𝑋 每一个取值都固定为 𝑥 时，𝑌的总体分布。

4.1.7 因果效应和因果效应差

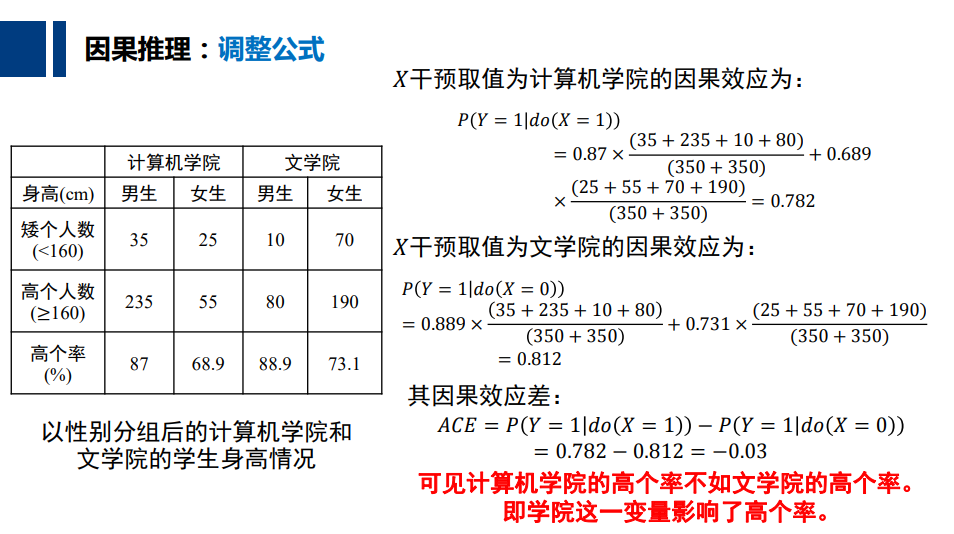
以两个学院学生身高与 学生性别所形成的因果图为例：

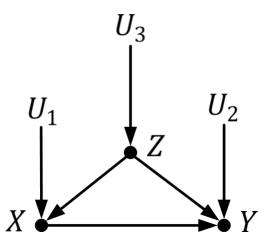
二值变量𝑋：学院(1表示计算机学院，0表示文学院)

二值变量𝑌：身高情况(1表示高个，0表示矮个)

二值变量𝑍：性别(1表示男生，0表示女生)

𝑈1,𝑈2,𝑈3：外生变量

为了分析两个学院学生高个率是否存在差别，可对学院 这一变量进行干预，即将𝑋取值固定为1或0。 设𝑑𝑜(𝑋 = 1)和𝑑𝑜(𝑋 = 0) 表示这两种干预，如下估计干预后产生的差别：$P(Y=1|do(x=1)) – P(Y=1|do(x=0))$​​，该式子被称为“因果效应差”(causal effect difference)或 “平均因果效应”(average causal effect, ACE)，$P(Y=y|do(X = x))$​​ 被称为因果效应(causal effect)。

4.1.8 操纵图模型和操纵概率

对学院变量𝑋进行干预并固定其取值为𝑥时，可将所有指向𝑋的边均移除。 因果效应$P(Y = y | do(X = x))$​ 等价于引入干预的操纵图模型(manipulated model)中条件概率$P_m(Y = y |X = x)$​​ 。

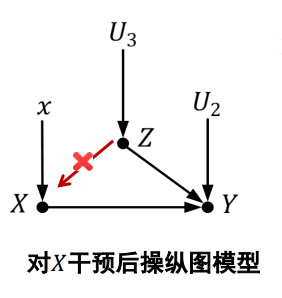
计 算 因 果 效 应 关 键 在 于 计 算 操 纵 概 率 (manipulated probability) $P_m$。$P_m$​​与正常(无干预)条件下概率𝑃在如下两个 面的取值不变：

• 边缘概率𝑃(𝑍 = 𝑧)不随干预而变化，因为𝑍的取值不会因为 去掉从 𝑍 到 𝑋 的箭头而变化 ， 即 ：$P_m(Z = z) = P(Z = z)$
• 条件概率$P(Y = y|X = x,Z = z)$不变，因为 Y 关于X和Z的函数 $f_Y = (X,Z,U_2)$未改变，即$P_m(Y=y|X=x,Z=z) = P(Y=y|X=x,Z=z)$​

4.1.8 调整公式

在干预图中， 𝑋和𝑍是𝑫-分离的，因此是彼此独立的，即：$P_m(Z = z|X = x) = P_m(Z = z) = P(Z = z)$。

因果效应

,该式子被称为调整公式（adjustment formula）。对于𝑍的每一 个取值𝑧，该式计算𝑋和𝑌的条件概率并取均值，这个过程称之为“𝑍调整”（adjusting for Z）或“𝑍控制” （controlling for Z）。该式的右端只包含正常(无干预)条件下的概率𝑃，即可用 正常(无干预)条件下的条件概率来计算干预后的条件概率。

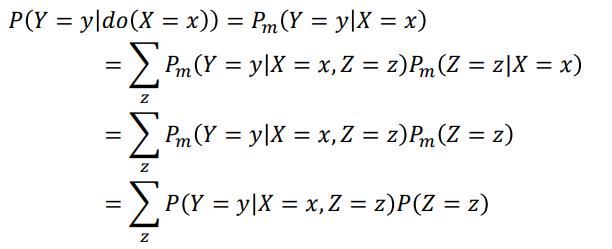
下面将调整公式用于计算对𝑋取值进行干预后计 算机学院/文学院高个子率，其中𝑋 = 1表示计算 机学院， 𝑌 = 1表示高个，𝑍 = 1表示表示男生， 则有：