一、评估模型

1.1 学会评估模型的重要性

在训练数据的时候，可能会发现模型的效果不是很好，于是就需要对模型进行调整，一般有以下几种方式：

• 使用更大的数据集（不一定有效，且代价很高）
• 尝试使用更少的特征（减少过拟合）
• 采用更多的特征，可以更好地拟合问题
• 增加多项式特征，比如 $x_1^2 \ \ x_1x_2$
• 尝试变小或变大正则化参数

然后这些方式的选取并不应该是随意的，而是应该有所依据的去选取，而在选择调整方法之前，首先要做的是对模型的性能进行评估，这也被称为“机器学习诊断法”，“诊断法”的意思是这是一种测试法 你通过执行这种测试能够深入了解某种算法到底是否有用 。 这通常也能够告诉你要想改进一种算法的效果什么样的尝试才是有意义的 。指的注意的是，学习和实现这些方法是很费时间的，但是这一切都是值得的，因为这可以帮助你在开发学习算法时节约很多的时间。

1.2 评估假设函数

划分训练集和测试集。

我们知道线性回归问题的目标是拟合训练集中的数据使得损失函数尽量地小，但是并不是说在训练集上的损失值越小就是越好的，因为可能出现了过拟合的现象，其表现为在训练集中的表现能力很好，而对于一个不在训练集中的数据的表现能力就很差，即模型的泛化能力较差。那么如何去判断是否出现了过拟合现象呢？对于下面这样一个简单的模型，我们可以画出图像，从图像中可以看出，曲线拟合了所有数据，出现了过拟合的问题，但是当参数量很多的时候，显然靠画图是无法看出模型是否发生过拟合的。

通常的做法是将数据集划分为训练集和测试集两类，比例通常为 7 ：3（训练集7，测试集3），所有我们只将数据集中的 70% 用于模型的训练，而剩下的用于测试模型，需要注意的是，如果数据集是按照某种规律或者顺序排列的，那么训练集和测试集的选取最好是打乱随机选取。在训练时，一般的做法是用训练集训练模型，最小化损失函数得到更新后的模型参数，然后用更新后的模型参数计算测试集的误差，测试集上的误差就可以用于评估模型的优劣。对于过拟合问题，其表现为在训练集上的误差小，而在测试集上的误差大。

1.3 模型选择问题

假如你要对一组数据采用线性回归模型， 你想知道最适合的多项式、最适合的特征个数以及最适合的正则化系数是多少等等，这样的问题被称为模型选择问题。假如我们要在下面这10个不同次数的模型中选取最优的，显然次数越高，模型越能拟合训练集，但这并不代表这样的模型泛化能力强，所以我们就需要交叉验证集来衡量哪种模型更好。

通常我们使用60% 的数据作为训练集，使用 20% 的数据作为交叉验证集，使用 20% 的数据作为测试集，一般训练模型的流程如下：

• 使用训练集训练不同参数的模型
• 分别将这些模型在交叉验证集上计算误差
• 选取最小误差的模型当做最终模型
• 在测试集上计算选出模型的误差，用于评估这个模型的泛化能力

这里需要明确测试集和验证集的意义，虽然两者都是用来衡量模型的性能，但是使用的时期不同。验证集是在挑选模型的时候使用的，即用于模型调优，而测试集是在所有的训练包括模型挑选都完成后进行的最终评估。形象地来说，训练集可以看成是平时的作业，验证集就是平时的小测试，而测试集就是最终的期末考试。之所以需要划分出那么多的训练集，就是为了避免模型拟合于某个数据集。具体来说，将数据集划分为测试集和训练集，就是为了衡量模型是够过拟合于训练集；在挑选模型的时候又划分出一个验证集，而不是直接用测试集来衡量，就是为了避免模型过拟合于测试集，导致选择了一个在测试集上误差很小，但是实际泛化能力很差的模型。需要注意的是，在模型训练的时候，一般测试集在整个过程中只会被使用一次。

二、偏差和方差

2.1 判别方法

当一个模型不尽人意到时候，多半可能是因为偏差太大或者方差太大，也就是说要么欠拟合要么过拟合了，如下图左就是高偏差大致欠拟合，右边是高方差导致过拟合，中间是比较合适的状态。

如下图是验证误差和训练误差关于多项式次数的函数，可以发现当次数越高时，训练误差会越小，而对于验证误差，先变小后变大。所以我们可以通过验证集和训练集的误差综合判断过拟合和欠拟合的现象，具体来说：

• 训练集和验证集误差都大（下图左边），则说明欠拟合
• 训练集误差小而验证集误差大，说明过拟合。

2.2 正则化

在我们在训练模型的过程中，一般会使用一些正则化（归一化）方法来防止过拟合。但是我们可能会归一化的程度太高或太小了，即我们在选择 $λ$ 的值时也需要思考与刚才选择多项式模型次数类似的问题。我们选择一系列的想要测试的 $λ$ 值，通常是 0 – 10 之间的呈现 2 倍关系的值（如0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10）。 我们同样把数据分为训练集 、交叉验证集和测试集。我们用上面介绍过选择模型的方法进行挑选，即：

• 使用训练集训练出 12 个不同程度归一化的模型
• 分别对交叉验证集计算的出交叉验证误差
• 选择得出交叉验证误差 最小 的模型
• 运用步骤 3 中选出模型对测试集计算得出推广误差

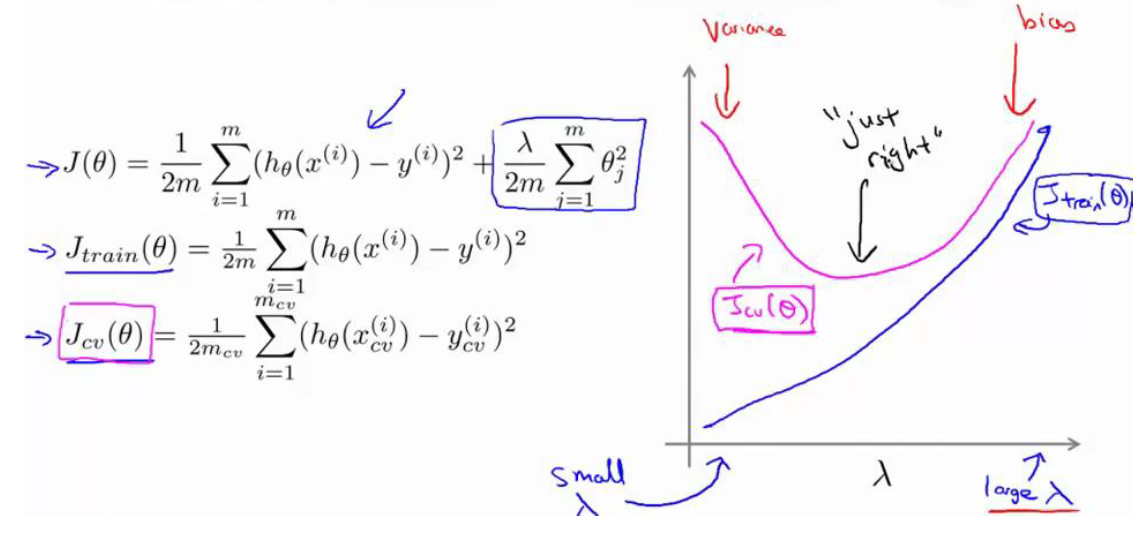
将 $\lambda$ 和误差的关系画出图像，观察可得：

• 当 λ 较小时，训练集误差较小（过拟合）而交叉验证集误差较大
• 随着 λ 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加

上述的结论也是很好理解的，正则化的目的就是减少过拟合，所以如果 $\lambda$ 太小就会导致过拟合，如果 $\lambda$ 过大，则会导致参数很小接近于0，这就会导致模型欠拟合。需要注意的是，正则化只会在模型训练时使用，而在测试和验证模型性能时，会去掉正则项。

2.3 学习曲线

学习曲线是一种很好的工具，用来判断某一个学习算法是否处于偏差、方差问题。 学习曲线是学习算法的一个很好的合理检验（sanity check ）。学习曲线是将训练集误差和交叉验证集误差作为纵坐标，横坐标为不同的训练集大小，以此来绘制曲线。
如下图是欠拟合的学习曲线，可以发现随着训练集的增加，交叉误差和训练误差逐渐靠近，并都保持在一个较高的水平，这说明，对于欠拟合问题，单纯地增加训练数据是没有用处的。

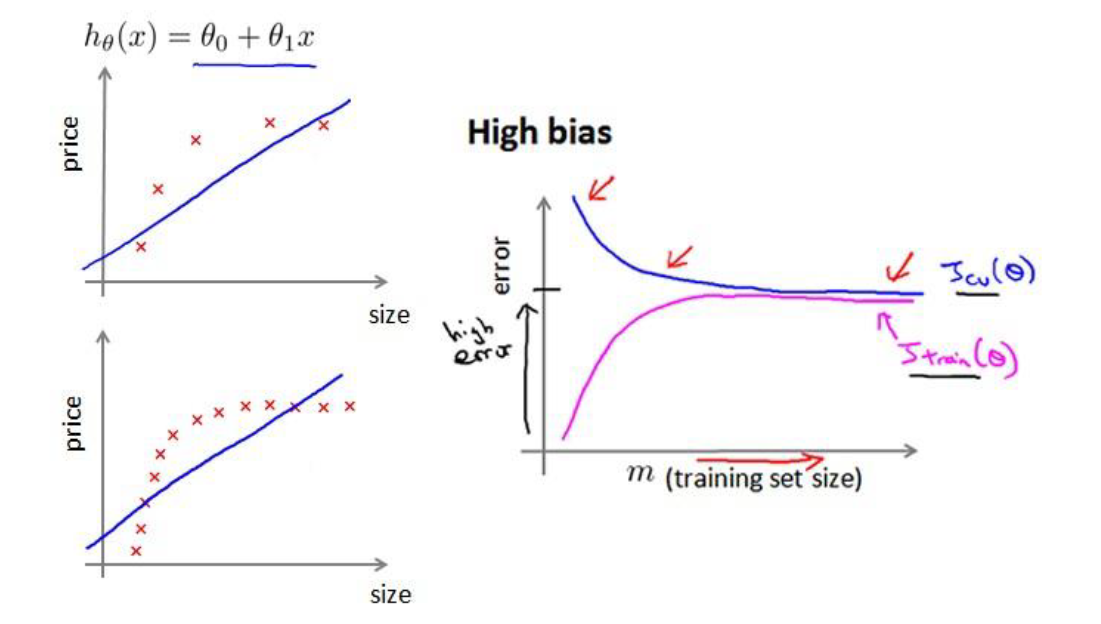
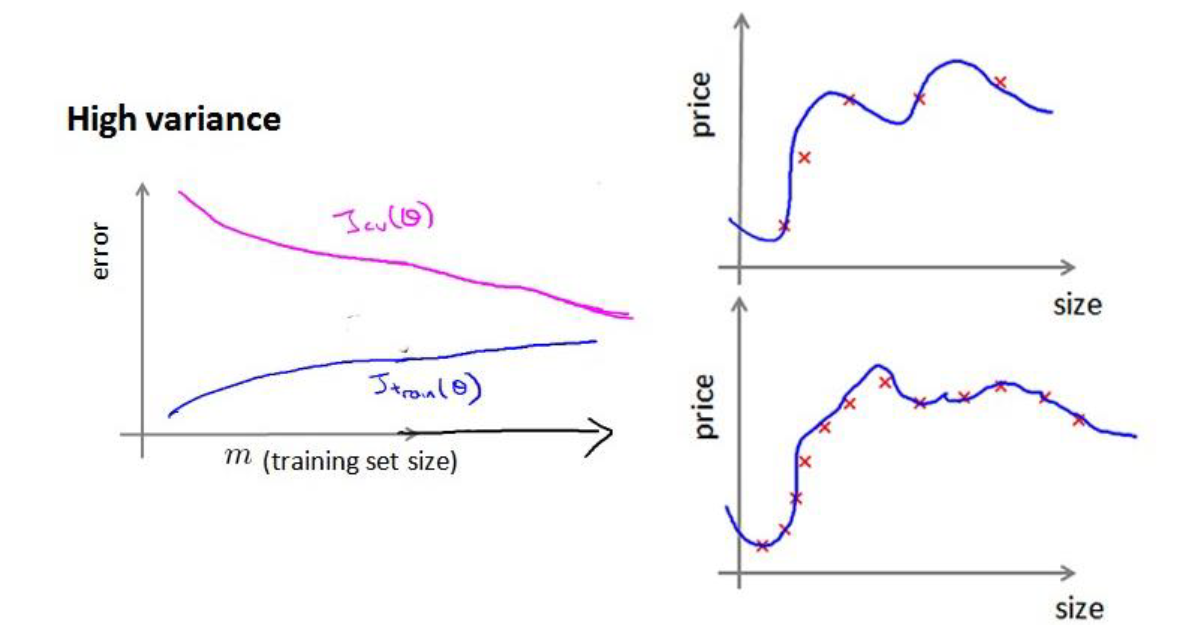
下图是过拟合的学习曲线，可以发现随着训练集的增加，交叉误差和训练误差逐渐靠近，并且交叉验证误差高于训练集，从这里可以看出，对于过拟合问题，增加训练集是可以提高模型效率的。

2.4 进行决策

对于前文提到的对模型的优化措施，现在可以得出在什么情况下选用什么措施了：

• 使用更大的数据集 —– 解决过拟合
• 尝试使用更少的特征 ——- 解决过拟合
• 采用更多的特征，可以更好地拟合问题 ——- 解决欠拟合
• 增加多项式特征，比如 $x_1^2 \ \ x_1x_2$ ——– 解决欠拟合
• 尝试变小或变大正则化参数 ——– 变小解决欠拟合，变大解决过拟合

对于神经网络出现的过拟合和欠拟合现象：

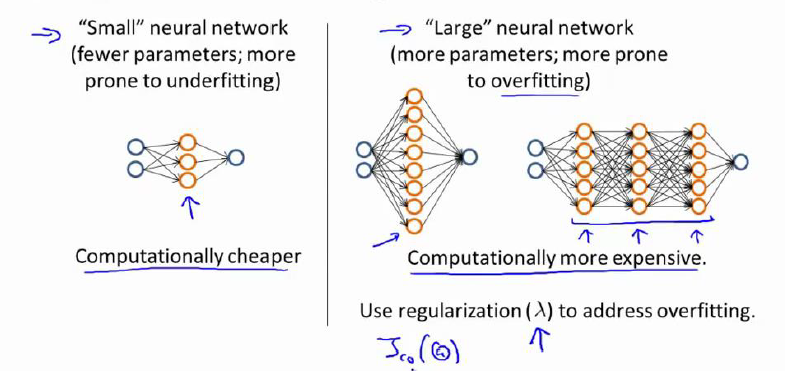
• 使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小
• 使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过归一化手段来调整而更加适应数据。

通常选择较大的神经网络并采用归一化处理会比采用较小的神经网络效果要好。通常情况下，神经网络使用一个隐藏层，如果需要使用多个隐藏层，可以分别训练含有不同隐藏层数量的神经网络，然后用验证集进行验证，选择验证误差最小的即可。

三、设计机器学习系统

3.1 首先需要考虑什么

在设计一个复杂的机器学习系统时，你会遇到很多问题，本章节将会给出一些关于如何巧妙构建一个复杂的机器学习系统的建议，以垃圾邮件分类器为例。首先要考虑的是决定如何选择并表达特征向量 $X$ ，我们可以选择一个由 100 个最常出现在垃圾邮件中的词所构成的列表，然后根据这些词是否在邮件中出现来获得特征向量（出现则为1，没出现则为0），为了构造这样一个分类器算法，我们可以进行“头脑风暴”，想出很多可能的优化方法：

• 收集更多的数据，让我们有更多的垃圾邮件和非垃圾邮件的样本
• 基于邮件的路由信息开发一系列复杂的特征
• 基于邮件的正文信息开发一系列复杂的特征，包括考虑截词的处理
• 为探测刻意的拼写错误（把 watch 写成 w4tch ）开发复杂的算法

但是这些设想，无论那一项都需要花费不少的精力和时间，能够准确地选择正确的方法就能节省大量的时间，随后的误差分析中，将会介绍一个系统性的工具来选取合适的方法。

3.2 误差分析

最推荐的解决机器学习问题的方法是：

• 快速实现一个简单的算法并训练，然后在验证集上进行测试
• 画出学习曲线，判断是过拟合还是欠拟合，决定是否需要更多数据还是更多属性等
• 进行误差分析：人工检查交叉验证集中我们算法中产生预测误差的实例，看看这些实例是否有某种系统化的趋势

误差分析并不总能帮助我们判断应该采取怎样的行动。有时我们需要尝试不同的模型，然后进行比较，在模型比较时，用数值来判断哪一个模型更好更有效，通常我们是看交叉验证集的误差。

3.3 类偏斜的误差度量

以癌症检测问题为例，假设我们有一个模型用于检测患者是否患有癌症，并且模型的错误率在1%，看起来这是一个很好的模型。但是，这里忽略了一个前提，就是训练集中，患有癌症的数据只占训练集的0.5%，也就是说，即时你的分类器对于所有的数据都预测没患癌症，你的准确率也能达到99.5%，这就说明在正样本和负样本占比极端的时候，单纯用准确率衡量模型是不可靠的。对于这种正负样本相差极端的类，我们称之为偏斜类。

对于含有偏斜类的情况，我们可以采用查准率（Precision）和查全率（Recall）来评判模型好坏。如下图，首先我们将模型预测结果分为四类：

• 正确肯定（ True Positive,TP ）：预测为真，实际为真
• 正确否定（True Negative,TN ）：预测为假，实际为假
• 错误肯定（False Positive,FP ）：预测为真，实际为假
• 错误否定（False Negative,FN ）：预测为假，实际为真

那么查准率 = $\frac{TP}{TP+FP}$ ，即预测正确的真样本占所有预测为真的比例。

查全率 = $\frac{TP}{TP+FN}$ ，表示预测正确的真样本占所有实际为真的比例。

3.4 查全率和查准率之间的权衡

还是以癌症检测模型为例，继续沿用刚才预测肿瘤性质的例子。假使，我们的算法输出的结果为 0或1，我们使用阀值 0.5 来预测真和假。但是因为癌症是一个噩耗，对一个人和家庭都会有毁灭性的大家，所有我们想要误诊率尽量低，可以通过提高输出为1的阈值来实现，比如将阈值提高到0.7，只有在输出结果大于0.7时才认为患癌症，这样查准率就会很高，查全率就会变低。相反，如果我们没有将一个潜在的患癌病人检测出来，就会耽误其治疗，所以我们也可能会向让查全率提高，那么我们就可以降低阈值，但是这样就会导致查准率变低。查全率和查准率之间的关系大致如下，图中有三根曲线，表示不同模型可能会有不同的走势，但是大致趋势相同。

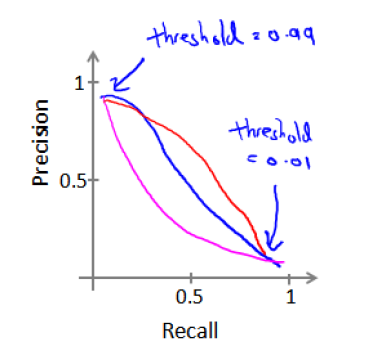
所以，改变阈值会同时对查准率和查全率造成影响，那么有没有什么办法可以帮助我们选择不同的阈值呢，我们可以使用 $F_1$ 值，其表达是为 $F_1 = 2\frac{PR}{P+R}$ ，其中 $P$ 表示查准率，$R$ 表示查全率。$F_1$ 的值越高，表示查全率和查准率都在一个较好的水平。

3.5 机器学习的数据

前面说到，单纯地去增加数据量不一定会对训练有帮助，那么在什么条件下，使用越多的数据，模型就会训练地越好呢？。 假设当前的特征值有足够的信息来预测 y 值，并且我们使用一种需要大量参数的学习算法，比如有很多特征的逻辑回归或线性回归或有很多隐藏单元的神经网络，这些算法都有很多的参数，可以拟合非常复杂的函数。很有可能，如果我们用这些数据运行这些算法，这种算法能很好地拟合训练集，因此训练误差就会很低了 。现在假设我们使用了非常非常大的训练集，在这种情况下我们尽管给模型设置了很多参数，但是如果训练集比参数的数量多很多，那么这些算法就不太可能会过度拟合 ， 也就是说训练误差有希望接近测试误差 。所以，使用大量数据的前提是，保证模型的特征值有足够的信息量，且我们有一类很好的函数。