CS231n第六节：训练神经网络（一）

传送门：Parts 1, 2, 3

本系列文章基于CS231n课程，记录自己的学习过程，所用视频资料为 2017年版CS231n，阅读材料为CS231n官网2022年春季课程相关材料

本文介绍了神经网络的构成。对于一个线性分类器，我们使用公式 $s = Wx$ 给每张图片计算一个类别得分，其中 $W$ 是一个矩阵， $x$ 表示输入向量，是由输入图片的每个像素拉直成一个向量得来的。比如使用CIFAR-10数据集， $x$ 是一个 [3072 * 1] 的列向量， $W$ 是一个 [10 * 3072] 的矩阵，所以输出是一个长度为10的向量，表示每个类别的得分。

而对于神经网络，一个简单的例子就是它会计算 $s = W_2max(0,W_1x)$ ，这里的 $W_1$ 是一个 [10 * 3072] 的矩阵，用于将输入图片转换成一个 100维的中间向量。 函数 $max(0,-)$ 是一个作用于每个元素的非线性函数，当然这里有很多种非线性函数可以选择，但是最常用和最简单的还是这个，也称为RELU。最终， $W_2$ 的大小为 [10 * 100] ，所以我们又将得到10个数字输出表示类别得分。指的注意的是，这里的非线性函数是不可或缺的，因为如果我们去掉非线性函数，那么两个矩阵可以合并成一个矩阵，那么这又变成了一个线性分类器了。$W_1,W_2$ 的值通过随机梯度下降学习得到，而梯度值通过链式法则，借助反向传播计算得到。

当然还有稍微复杂一点的网络，比如三层网络 $s = W_3max(0,W_2max(0,W_1x))$ ，这里的 $W_1,W_2,W_3$ 也是学习得到的参数，而中间隐藏层的个数是网络的超参数。现在让我们研究如何从神经/网络的角度来解释这些计算。

1. 神经元

1.1 生物学启发和关联性

神经网络最初受到生物神经系统启发得来，并逐渐脱离生物神经系统，演变成一个工程问题，并在机器学习任务中实现了很好的结果。不过，我们还是简单地介绍一下生物神经系统。大脑的最基本的计算单元是神经元。人类的神经系统中有大约860亿个神经元，并且由大约1e14-1e15个突触 （synapses）相连。如下图左是一张生物神经元的示意图，右边是一个神经元的数学建模。每个神经元会接受来自 树突（dendrites）的输入信号，然后沿着轴突（axon）产生输出信号。轴突最终会产生分支并和其他神经元的树突通过突触相连。在神经元的数学模型中，来自其他神经元轴突的信号（比如 $x_0$）与当前神经元的树突通过突触基于突触上的强度（比如 $w_0$）进行乘法形式的交互（比如 $w_0x_0$）。这一方法中，突触的强度 $w$ 是可以学习的，通过控制强度（以及方向，比如正面影响还是负面影响）来影响其他某个神经元。在这一基础模型中，树突将所有输入的信号带到细胞体中，并将它们全部相加。如果最终的总和大于某个门槛值，那么这个神经元将会被激活，将会沿着轴突发出激活信号。在计算模型中，我们假设准确的激活时间不重要，只有激活的频率表示通信的信息。基于这一频率编码的解释，我们建模出了激活频率，即激活函数 $f$ ，用于表示轴突发出激活信号的频率。在历史上，最常用的激活函数时sigmoid函数，它会将输入压缩在0-1的范围内，以实数的形式输出。后面我们将看到关于这个函数的细节。

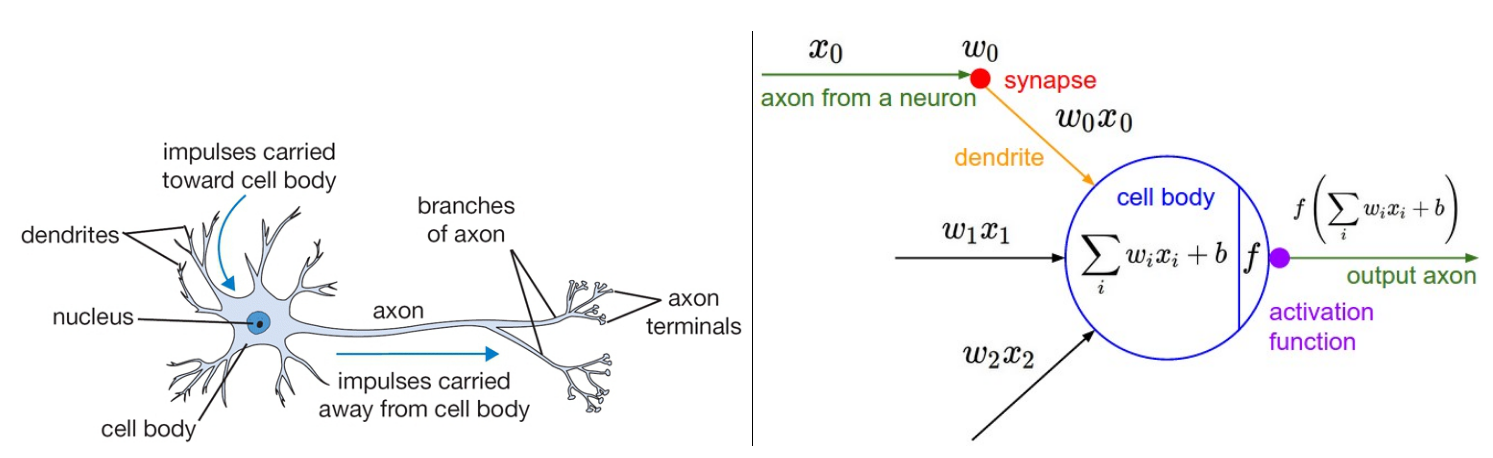
对于单个神经元的前序传播的代码示例如下：

class Neuron(object):
  # ... 
  def forward(self, inputs):
    """ assume inputs and weights are 1-D numpy arrays and bias is a number """
    cell_body_sum = np.sum(inputs * self.weights) + self.bias
    firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid activation function
    return firing_rate

也就是说，每个神经元将输入和它的权重进行点积，然后加上偏置项，经过非线性函数（激活函数）的处理，得到最终结果。

粗糙的抽象模型：

需要强调的是，上面介绍的生物神经元模型是非常粗糙的，比如说实际上有很多种不同类型的神经元，每个都有不同的特性。生物神经元中的树突使用了复杂的非线性计算，突触上也不只有一个权重，他们都是一个复杂的非线性的动态系统。由于所有这些和许多其他简化，有真正的神经科学背景的人可能会对这样一个简化的类比有很多的不满。

1.2 使用单个神经元作为线性分类器

神经元的前向传播在数学形式上看起来和线性分类器十分类似。正如我们在线性分类器中看到的那样，一个神经元有喜欢（激活）或不喜欢（不激活）某个其输入空间的线性区域的能力。因此，使用恰当损失函数作为神经元的输出，我们可以将单个神经元转变成一个线性分类器：

二元Softmax分类器：

比如，我们可以将 $\sigma\left(\sum_{i} w_{i} x_{i}+b\right)$ 解释成某一类别的概率 $P\left(y_{i}=1 \mid x_{i} ; w\right)$ ，另外一个类别的概率可以表示成 $P\left(y_{i}=0 \mid x_{i} ; w\right)=1-P\left(y_{i}=1 \mid x_{i} ; w\right)$，因为概率之和为1。在这种解释下，我们可以使用交叉熵损失函数作为线性分类器的损失函数，然后对其进行优化，使其变成一个二元softmax分类器（又称为logistic回归）。由于sigmoid函数的值域在0-1之间，所以这个分类器的预测结果取决于神经元的输出是否大于0.5。

二元SVM分类器：

同样，我们可以使用最大边界铰链函数（max-margin hinge loss）作为神经元的输出，并将其训练成一个二元的SVM分类器。

正则化解释：

无论是SVM还是softmax，他们的正则化损失在生物视角下可以解释成逐步遗忘，因为在每个参数更新后，损失函数都具有将所有突触权重驱动到零的效果。

1.3 常用的激活函数

Sigmoid函数

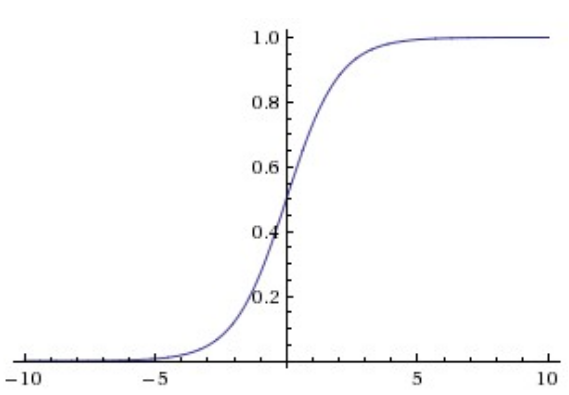
Sigmoid函数的数学表达形式为：$\sigma(x)=1 /\left(1+e^{-x}\right)$，它接受一个实数并将其压缩到0-1的范围内，其中大的负数将会变成0，而大的正数将会变成1。在历史上，sigmoid函数被经常使用到，因为它对神经元的激活有很好的解释性：从完全未激活的状态0，到完全饱和的激活状态1。实际上，sigmoid函数正在逐渐退出舞台，因为它有一下两个主要的缺点：

• 导致梯度饱和或消失： 使用了sigmod函数的神经元有一个非常不期望的性质就是当神经元的状态处于无限接近0或1的时候，它的梯度基本为0。而在反向传播的时候，这个局部梯度将会和上游传来的梯度进行相乘。因此，如果局部梯度非常小，那么它将“杀死”梯度，使得几乎没有信号从这个神经元中传出。此外，初始化的时候也需要保持谨慎，以防止一开始的时候神经元就出现梯度消失的问题。

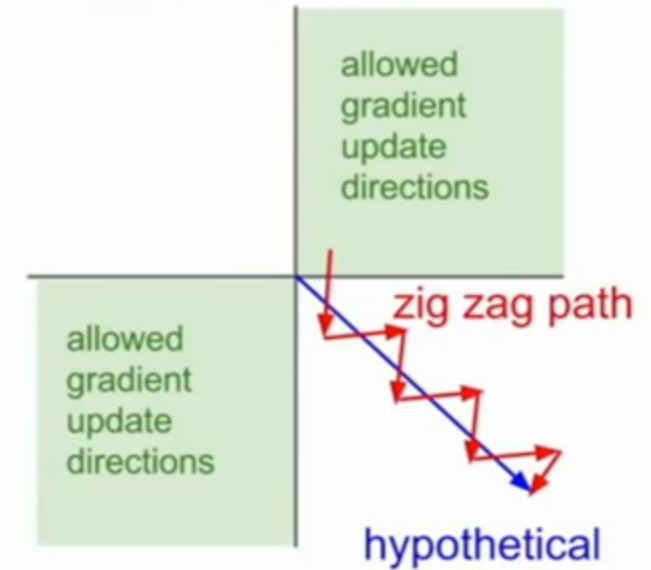
• 值域不是零均值化的（zero-centered）： 神经网络中的神经元接受来自前面层的非零均值化的输入是不愿被看到的。这对梯度下降期间的灵活性有影响，因为如果输入的数据一直保持正的，那么在反向传播时，权值 $w$ 的梯度将会全部为正或全部为负（取决于上游传来的梯度正负）。这就导致根据梯度更新参数时产生Z字抖动，如下图，即只能朝着两个特定的方向移动，不能朝着正确的方向移动。因此，这是一种低效率的现象，但与上面的问题相比，它的严重后果较小。

  

Tanh函数

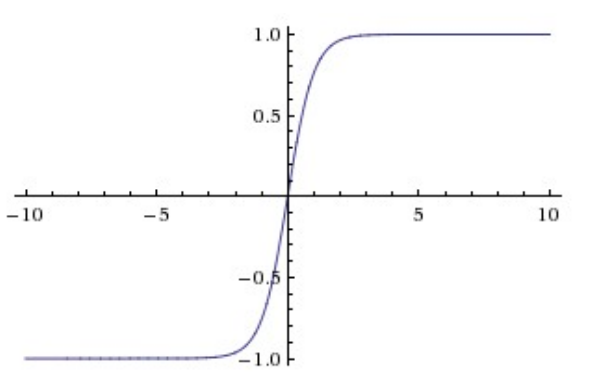
Tanh函数将输入的数压缩到 [-1,1] 内，这改善了sigmoid的第二个缺点，因为它的输出是零均值的，这就使得梯度可正可负，但任然不能解决梯度消失的问题。值得注意的是，tanh其实就是被缩放了的sigmoid，因为 $\tanh (x)=2 \sigma(2 x)-1$

ReLU函数

下图左是ReLU函数图像，右图是来自论文 Krizhevsky et al. 中将ReLU的训练效果与Tanh的比较，有6倍的提升。

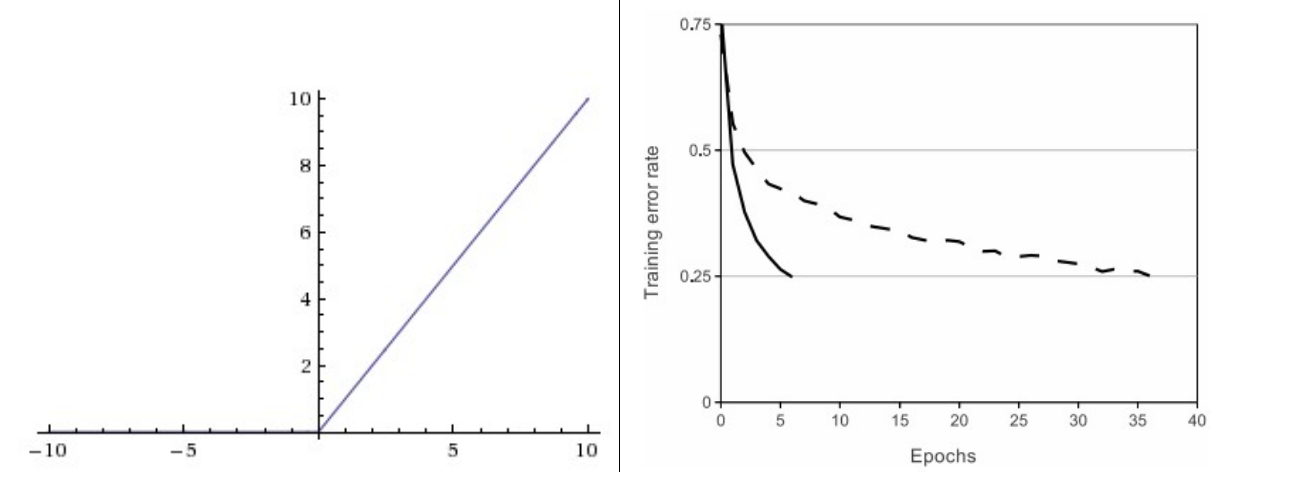
ReLU全称为Rectified Linear Unit，整流线性单元，这在最近几年非常流行。它的公式为 $f(x) = max(0,x)$ ，换句话说，激活与否的门槛被简单得设置成了0，ReLu函数有以下几个优劣：

• 大大加速收敛速度： 与Tanh和Sigmoid相比，ReLU在随机梯度下降时的收敛速度更快，有人认为这是由于其一半线性一半不饱和形式所致。
• 更高效： 与Sigmoid和Tanh相比，ReLU函数的计算速度更快。
• 较为脆弱： 不幸的是，使用ReLU的神经元在训练的时候比较脆弱，容易“死亡”。比如说，如果有一个很大的梯度通过ReLU神经元，而如果你的学习率设置的也非常大，那么这就会导致你的权重被更新过头了，变成一个很小的负数。由于权重为负，那么如果输入的值为正数（一般都为正数），那么输出也为负数，经过ReLU函数后就变成了0，此时，反向传播时会发现该神经元的梯度为0，那么这个神经元的权值永远不会被更新。这种情况发生，那么该神经元的梯度将永远变为0。也就是说，在训练过程中，某些神经元可能会不可逆转地死亡。比如说，如果学习率设置过高，你会发现有大约40%的神经元死亡，当然用恰当的学习率可以使得这一情况很少发生。

Leaky ReLU

Leaky ReLU函数是对解决ReLU神经元死亡的一种尝试。与ReLU对负数全变为0不同，leaky ReLU给负半边一个很小的正斜率，也就是说，表达式变成 $f(x) = \left\{\begin{matrix} x (x>=0) \\ \alpha x(x<0) \end{matrix}\right.$ ，其中的 $\alpha$ 是一个很小的常数。有些人报告了这种激活函数的成功，但结果并不总是一致的。此外，负半边区域中的斜率 $\alpha$ 也可以成为每个神经元的一个参数进行学习得来，这就是PReLU，可见Delving Deep into Rectifiers。

Maxout

还有一种激活函数的使用形式不是 $f(w^Tx+b)$ ，而是在参数和输入数据进行点乘的时候使用。比如说Maxout激活函数，它实际上是个一种ReLU和Leaky ReLU的一般化版本。Maxout使用 $\max \left(w_{1}^{T} x+b_{1}, w_{2}^{T} x+b_{2}\right)$ 来计算输出。可以发现，ReLU和Leaky ReLU都是这种形式的一种特殊形式（比如说ReLU就是 $w_1=0,b_1=0$ 的时候）。因此，Maxout在拥有ReLU和Leaky ReLU优点的同时没有两者的缺点。唯一不足之处在于，它需要两倍的参数。

以上就是最常见的神经元类型及其激活功能的讨论。最后，我们很少在同一个神经网络中混合使用不同的激活函数，虽然这样没有任何问题。

Tips： 如何挑选激活函数呢？使用ReLU函数，并小心选择学习率，时刻关注神经网络中死亡的神经元。如果这无法优化， 尝试Leaky ReLU或者Maxout，永远不要使用sigmoid，可以尝试Tanh，但一般不会有更好的效果。

2. 神经网络结构

2.1 层状结构

神经网络是以神经元组成的图：

神经元以无环图相连形成一个神经网络。换句话说，一些神经元的输出会作为一些神经元的输入。环状结构是不允许出现在神经网络中的，因为这回使得前向传播时出现无限的循环。神经网络中的神经元一般以几个不同的层的形式组织起来。对于一般的神经网络，最常见的层就是全连接层，两个相邻的全连接层中的每个神经元都和其他层中的所有神经元相连，但是同一层中的神经元不会相互连接。如下图是两种全连接的神经网络的示意图：

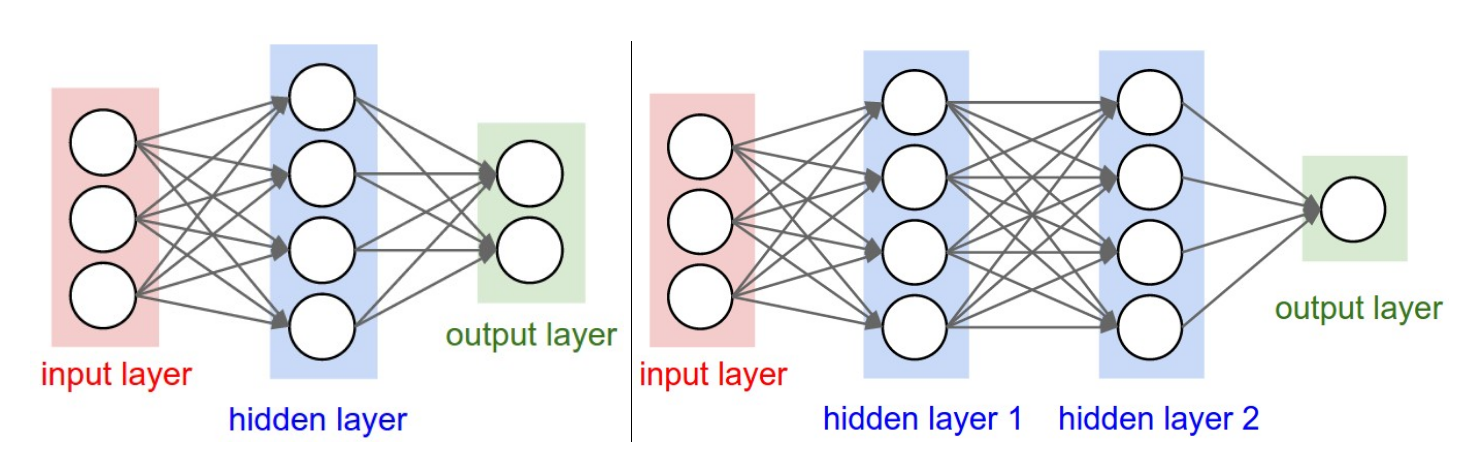
命名规范：

一般来说我们说的n层神经网络是不包括输入层的，因此，单层神经网络用来描述没有隐藏层只有输出层的神经网络。在这种意义上来说，你可以听到有时候人们会说logistic回归和SVM是一种特殊的单层神经网络。你可能还会听到这类网络被描述成：Artificial Neural Networks ANN 人造神经网络，Multi-Layer Perceptrons MLP多层感知机。许多人不喜欢神经网络和真正的大脑之间的类比，而是更喜欢将神经元称为单位。

输出层：

不同于神经网络中的其他层，输出层的神经元一般不会包含激活函数，因为最后一层的输出一般用于表示不同类别的得分，一般是任意的实数。

计算神经网络的大小：

人们一般使用两个指标来计算神经网络的大小，即神经元的个数，或者更常用的是参数个数，下面计算上图网络中的这两个指标值：

• 左图，有 $4+2=6$ 个神经元（不计算输入层的神经元），有 $3*4+4*2=20$ 个权重， $4+2 = 6$ 个偏置，一共 $26$ 个参数。
• 右图，有 $4+4+1=9$ 个神经元（不计算输入层的神经元），有 $3*4+4*4+4*1=32$ 个权重， $4+4+1 = 9$ 个偏置，一共 $41$ 个参数。

作为比较，卷积神经网络一般有1亿个参数，一般由10-20层组成，并且由于权值共享，实际有效的连接会更多。

2.2 前向传播示例

矩阵乘积与激活函数重复地交织在一起：

神经网络被组织成层状结构的其中一个主要原因是这一结构使得使用矩阵乘法来评估神经网络变得更为简单和高效。如上图中的右图3层神经网络，输入是一个 $[3*1]$ 的向量。全部的神经元之间连接的权值可以被存放在一个矩阵中。比如说，第一个隐藏层的权重 $W_1$ 将是一个 $[4*3]$ 的矩阵，并且所有偏置项可以组成一个 $[4*1]$ 的向量 $b$ 。这里，每个神经元的全部权重表示成了 $W_1$ 的一列，所以这一层的输出可以用点乘 np.dot(W1,x) 来表示。如下是使用矩阵乘法进行前向传播的过程：

# forward-pass of a 3-layer neural network:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
x = np.random.randn(3, 1) # random input vector of three numbers (3x1)
h1 = f(np.dot(W1, x) + b1) # calculate first hidden layer activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # calculate second hidden layer activations (4x1)
out = np.dot(W3, h2) + b3 # output neuron (1x1)

2.3 表达能力

有一种说法是，使用全连接层的神经网络可以看成通过权值来参数化得定义了一系列的函数。那么这一系列的函数的表达能力如何呢？换句话说，是否存在一个函数时不能由神经网络表示的？

其结论是，包含至少一个隐藏层的神经网络是一个通用的近似表达器（universal approximator）。也就是说，对于任意一个连续的函数 $f(x)$ ，以及$\epsilon>0$ ，存在一个拥有一个隐藏层的神经网络 $g(x)$ ，可以保证 $\forall x,|f(x)-g(x)|<\epsilon$ ，换句话说，神经网络可以近似表达任何连续函数。可以参考 Approximation by Superpositions of Sigmoidal Function 或者 intuitive explanation。

如果一个隐藏层足以近似任何函数，为什么要使用更多的层使得网络更深呢？答案是，两层神经网络是通用的近似值，是一个在数学上很可爱但在实际应用中较弱且无用的事实。比如 sum of indicator bumps 函数 $g(x)=\sum_{i} c_{i} 1\left(a_{i}<x<b_{i}\right)$，也是一种通用近似表达器，但是没人会将其用于机器学习中。神经网络在实践中效果很好，因为它们可以简洁地很好地表示一个平滑函数，并且可以很好地表示出我们在实践中遇到的数据的统计特性，同时我们可以很简单地使用优化算法（比如梯度下降）。同样的，尽管单个隐藏层的神经网络和更深的神经网络的表达能力是相同的，但是实际上更深的网络的效果会更好。

此外，通常在实际应用中3层的网络效果比2层的更好，但是更深的网络所带来的增益就很小了。这和卷积神经网络不同，在卷积神经网络中，深度对于一个好的识别系统是非常重要的。对于此现象的一种解释是，图片拥有分层的结构（比如说脸是由眼睛组成的，而眼睛又是由一些边缘组成的），所以层数对于这样的数据域具有直观的意义。

2.4 设置层数和每层的大小

面对一个实际问题，我们应该如何去构造一个网络呢？我们需要使用隐藏层吗？需要使用几个隐藏层？每层应该设置成多大？首先，我们需要知道的是，当我们增加模型的层数和每层的大小时，模型的能力都会有所增加。也就是说，可以表达的函数空间增加了，因为神经元相互合作可以表达很多不同的函数。比如说，假设我们在二维空间中有一个二元分类问题，我们可以训练三个不同的网络，每个神经网络都只有一个隐藏层，可视化结果如下，此结果可以在 ConvNetsJS demo 中自己训练得到：

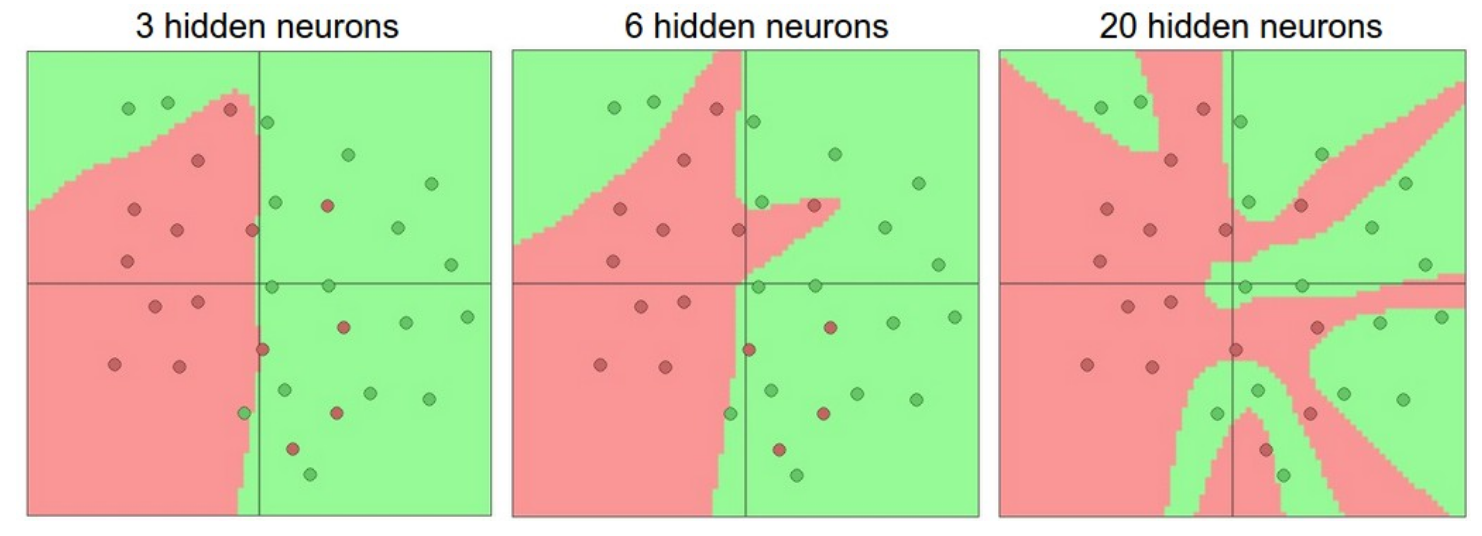
在上图中，我们可以看到，同样层数的神经网络，使用更多的神经元可以表示更复杂的函数。不过，但是，这既是祝福（因为我们可以学会对更复杂的数据进行分类），又是诅咒（因为它很容易在训练集中发生过拟合）。过拟合现象一般发生在模型具有很强的能力，于是可以拟合数据中的噪音，而不是拟合数据间潜在的关系。比如，具有20个隐藏神经元的模型符合所有训练数据，但代价是将空间细分为了许多不相交的红色和绿色决策区域。具有3个隐藏神经元的模型仅具有对数据的宽泛的表达能力。它认为数据由两部分组成，少量在绿色区域中的红点被认为是一些噪音。在实际中，这样的分类器在测试集中具有较好的泛化能力。

基于上面的讨论，如果数据不是很复杂，为了防止过度拟合，则似乎可以优选较小的神经网络。不过，这是不正确的，这里有很多其他的方法用于避免过拟合。在实践中，使用这些方法来防止过拟合比减少神经元个数的方法更好。

背后的微妙原因是，较小的网络很难使用局部方法（例如梯度下降）进行训练：显而易见的是，他们的损失函数之间只有相对少的局部最小值，并且这些局部最小值很容易造成收敛，这不是一件好事（因为会伴随很大的loss）。相反的，使用更大的神经网络将会包含更多重要的局部最小值，这些局部最小值会比它们实际的损失值更好。实际上，如果你训练一个小型的网络，那么最终的损失值会呈现出一个很大的差异，因为有时候你比较幸运收敛到了一个较好的局部最小值，而有时候你运气比较差，收敛到了一个不太好的局部最小值。另外一方面，如果训练大型的网络，你会发现你可能会有很多种解决方案，但是最终损失值的差异都会很小。换句话说，所有的解决方法效果都是一样好的，并且更少地依靠于一开始的随机初始化的运气。

再次声明，控制正则化强度是一种更好的控制过拟合的方法，而不是控制神经元的个数。从下图可以观察，不同正则化强度的差异：

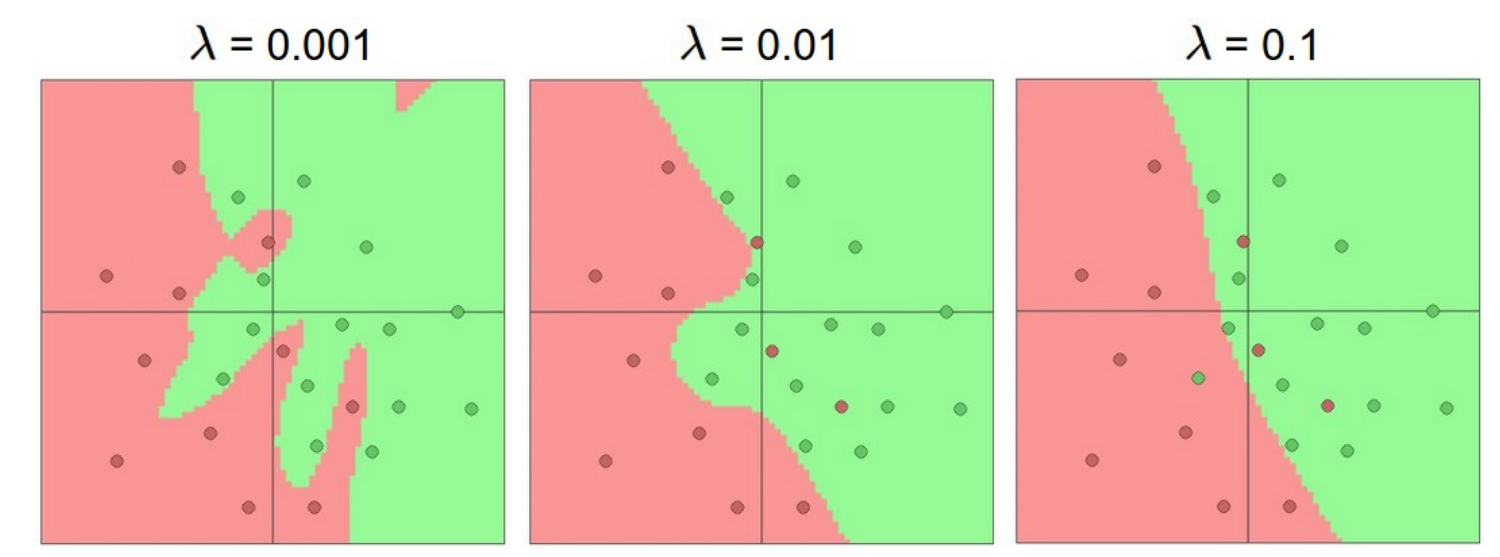
关键点在于，你可能害怕发生过拟合而使用较小的网络，这是不正确 。取而代之的是，你应该按照设备的计算能力来设计足够大的神经网络，并使用其他正则化技术来控制过度拟合。