本文为论文Rotated Binary Neural Network的精读总结，该论文发布于NeurIPS 2020，提出了RBNN，通过旋转来缩小二值化后的误差，效果较好。文中部分表述为原文翻译，所有图片除非特别注明，都来自原论文。本文在多平台同步，进入主站获得更好体验。

论文链接：https://arxiv.org/abs/2009.13055

作者：Mingbao Lin, Rongrong Ji, Zihan Xu, Baochang Zhang, Yan Wang, Yongjian Wu, Feiyue Huang, Chia-Wen Lin

代码链接：https://github.com/lmbxmu/RBNN

1. Introduction

1.1 DNN介绍

DNN（deep neural networks）在计算机视觉任务中取得了很好的效果，比如图像分类、目标检测、实例分割等。不过，大量的参数和计算的复杂度带来的高存储和高计算性能的限制，使得DNN很难应用在一些低性能的设备上。为了解决这个问题，提出了很多压缩技术：network pruning，low-rank decomposition，efficient architecture design，network quantization。其中，network quantization将全精度（full-precision）网络中的权重和激活值转换成低精度的表达。其中一个极端的情况就是 binary neural network（BNN 二值神经网络），它将权重和激活值的数值限制在两个取值：+1和-1。如此，相比全精度的网络，BNN的大小可以缩小32倍（全精度网络中一个双精度数值用32bit表示，BNN中一个数值用1bit表示），并且使用乘法和加分的卷积运算可以使用更高效的 XNOR 和 bitcount 运算代替。

1.2 BNN介绍

BNN中的卷积运算如下图所示（图源自 Binary Neural Networks: A Survey ），XNOR表示同或门，即值相同为1，不同为0，由于BNN中只有+1和-1两种数值，所以将-1看做0进行运算，对照真值表我们可以发现，对取值为+1和-1的两个变量进行乘法运算，等价于对其进行XNOR运算，于是就可以用XNOR代替卷积中的乘法运算。下面我们要将XNOR的结果相加，这里使用bitcount来代替加法运算。bitcount表示计算输入中1的个数，下图中对xnor的结果进行bitcount，得到1的个数为3，并且卷积核的大小是已知的（这里为9），我们就可以计算出XNOR运算后的求和结果：$-(9-3)+3=-3$。因此，卷积可以用XNOR和bitcount代替，而这两个运算在实现上比乘法和加法更加高效。

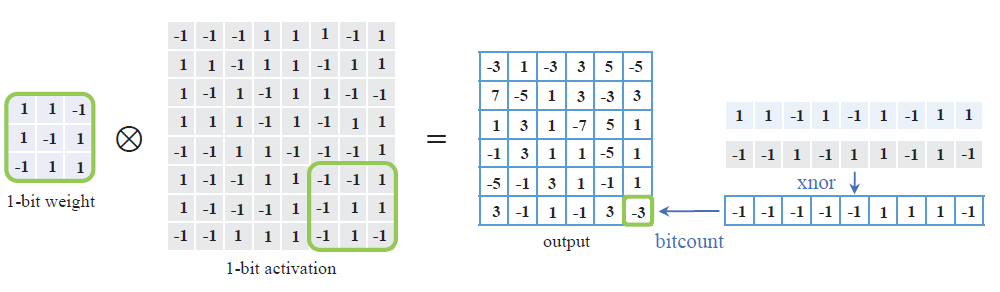
1.3 目前难点

基于上述的两个优点，BNN受到了大量的关注，不过BNN还有一个难点就是如何缩小全精度神经网络和其二值化后版本的误差。一个主要的问题就是全精度的权重向量 $w$ 和二值化后的向量 $b$ 之间的巨大的量化误差（如下图a）。解决这个问题，目前SOTA的方案是通过在每一个 channel 中引入一个可学习的放缩因子 $\lambda$ （XNOR-Net和IR-Net），即：

不过 $\lambda$ 的引入只减少了一部分量化误差，因为它的目标是最小化全精度权重和二值化权重的L2范数距离，但是并没有改善角度偏差导致的误差（如下图b所示），也就是说，当 $\lambda \mathbf{b}-\mathbf{w}$ 和 $\lambda \mathbf{b}$ 正交时（即图中 $\lambda\mathbf{b}$ 和虚线垂直时），$\|\lambda \mathbf{b}-\mathbf{w}\|^{2}$ 的值最小，由此可知：

所以，$\|\mathbf{w} \sin \theta\|^{2}$ （即图中虚线向量的模长）就是量化误差的下界，如果角度偏差 $\theta$ 很大，那么就会导致量化误差的下界很大，且这是无法通过上述的方法解决的问题。

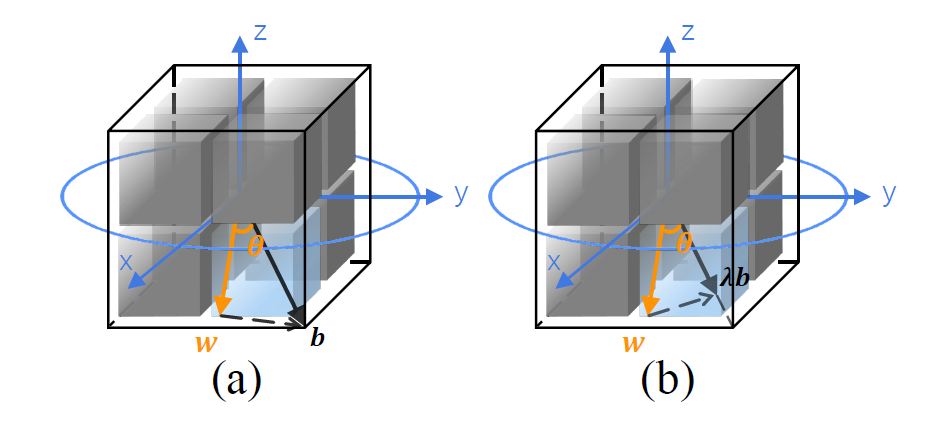
并且，论文中指出，角度偏差$\theta$ 很大的情况出现的概率很大。如下图a表示RBNN和XNOR两种BNN使用ResNet-20作为网络架构时，第1层到第18层的二值化前后向量的余弦相似性，b图表示量化误差。余弦相似性就是两个向量夹角的cos值，越接近1表示两个向量的夹角越小，从下图a中可以看出XNOR的余弦相似性在0.6-0.7之间，说明夹角较大，角度偏差在每一层都存在且不可忽视。从图b中可以看出，XNOR的量化误差在浅层和深层网络中的误差较大。而RBNN在角度偏差和量化误差上都有较好的表现。

此外，BNN通过学习可以获得的信息上限为 $2^n$ ，其中 $n$ 表示BNN中参数的个数，$2$ 表示BNN中的两种可能的取值。Weight flips（权重翻转）表示权值从+1变成-1，或者反之。当翻转的概率达到50%时，BNN的信息熵达到最大限度 $2^n$ 。但是，使用放缩因子 $\lambda$ 只会使得少量的权重发生翻转，因此BNN在训练过程中获得的信息就很少。

个人理解： 当翻转的概率为50%时，无论初始权重中+1和-1的分布比例是多少，在以50%的概率翻转后都会平均分布，此时类似于质量均匀的硬币，此时的不确定性最大，信息熵就最大。

1.4 解决方案

论文中提出了 Rotated Binary Neural Network (RBNN) 来减少由角度偏差带来的量化误差。论文中一共提出了4个新的技术：首先是提出了一个角度对齐方案（angle alignment scheme），通过学习一个旋转矩阵，在每一个训练的epoch前将将全精度权重向量旋转到其二元超立方体的几何顶点上。为了降低时间和空间的复杂度，论文中没有直接学习一个大的旋转矩阵，而是介绍了一个 bi-rotation formulation 来学习两个较小的矩阵作为代替。于是，就可以交替进行优化的步骤，学习旋转矩阵和二值化参数矩阵，以此减小角度偏差带来的量化误差和二值化前后的模长误差。此外，为了摆脱优化过程中陷入局部最优解的可能性，论文中在训练时，还会动态调整旋转矩阵的参数。上述提出的旋转方案不仅可以减小角度偏差带来的量化误差，还能实现大约50%的权重翻转的概率，以此获得最多的信息。最后，论文中还提出了一个 training-aware approximation of the sign function 用于反向传播时计算梯度。

2. Approach

2.1 BNN

对于一个CNN网络，我们定义第 $i$ 层的权重和特征图为$\mathbf{w}^{i} \in \mathbb{R}^{n^{i}}$，$\mathbf{a}^{i} \in \mathbb{R}^{m^{i}}$，其中 $n^{i}=c_{\text {out }}^{i} \cdot c_{i n}^{i} \cdot w_{f}^{i} \cdot h_{f}^{i}$ ，$m^{i}=c_{\text {out }}^{i} \cdot w_{a}^{i} \cdot h_{a}^{i}$，$c_{out}^{i},c_{in}^{i}$ 分别表示输出和输入的channel个数，$\left(w_{f}^{i}, h_{f}^{i}\right) \text { and }\left(w_{a}^{i}, h_{a}^{i}\right)$ 分别表示卷积核和特征图的宽和高。因此，我们有：

$\circledast$ 表示一个标准卷积，这里为了简便省略了激活层。BNN会将 $\mathbf{w}^i$ 和 $\mathbf{a}^i$ 转换成 $\mathbf{b}^i_w$ 和 $\mathbf{b}_a^i$，其取值为 $\{-1,+1\}$ ，如此可以将卷积转换成高效的xnor和bitcount操作，我们使用下式进行前向传播：

其中 $\odot$ 表示xnor和bitcount操作，$\text{sign}(\cdot)$ 表示 sign 函数，如果输入为正数则输出1，否则输出-1，$\mathbf{b}_{w}^{i} = \text{sign}(\mathbf{w}^i)$ ，并且可以使用一个缩放因子来改善norm difference，但是正如Introduction中介绍的，使用缩放因子无法改善由角度偏差带来的误差。并且，使用缩放因子，会使得 $\mathbf{w}^i$ 和 $\mathbf{b}^i_w$ 的方向相同，也就很难造成权重翻转，无法学到很多的信息。下面将介绍一些方法，可以在改善角度偏差的同时提升权重翻转的概率。

2.2 RBNN

 

考虑在每一个训练epoch开始前，对 $\mathbf{w}^i$ 采用一个旋转矩阵 $\mathbf{R}^i\in\R^{n^i\times n^u}$，使得旋转后的权重向量 $(\mathbf{R^i})^T\mathbf{w}^i$ 和二值化后的向量 $\text{sign}((\mathbf{R^i})^T\mathbf{w}^i)$ 的角度偏差 $\varphi^{i}$ 最小。对于两个 $\vec{a}$ 和 $\vec{b}$ 向量， 我们知道他们之间的夹角的 cos 值可以通过下列公式得到：

同时，两向量夹角的cos值也称为两向量的余弦相似性，用于评判两个向量角度距离，值越接近1表示角度越小，代入到二值化前后的向量中，可以得到角度偏差：

其中 $\mathbf{I}_{n^{i}}\in\R^{n^i\times n^i}$ 表示一个n阶的单位矩阵，此约束条件表示旋转矩阵 $\mathbf{R}^i$ 表示一个正交矩阵，这也是旋转矩阵的条件之一（具体性质和推导不太清楚）。 并且由于二值化后取值仅由+1和-1，而L2范数计算方式是将向量的每一个元素取平方和后开方，所以 $\left\|\operatorname{sign}\left(\left(\mathbf{R}^{i}\right)^{T} \mathbf{w}^{i}\right)\right\|_{2} = \sqrt{n^i}$ ，即元素个数总和再开平方。而旋转前后不会改变向量的模长，所以 $\left\|\left(\mathbf{R}^{i}\right)^{T}\mathbf{w}^{i}\right\|_{2}=\left\|\mathbf{w}^{i}\right\|_{2}$（这里可能可以从旋转矩阵的性质出发推导证明，但是目前不太清楚，论文中也没进行解释，只想到了这样一个比较合理的解释，如有错误，请指正）。并且，这两项都是常数，$\sqrt{n^i}$ 是常数不用说，$\left\|\mathbf{w}^{i}\right\|_{2}$ 之所以也是常数，是因为每次只在每个训练的epoch的最开始进行旋转，而不是训练的过程中，所以可以视作常数。于是我们令：

我们可得：

这里的推导用到了两个性质：$\mathbf{a}^T \mathbf{b}= \text{tr}(\mathbf{a} \mathbf{b}^T)$，其中 $\mathbf{a} \in \R ^{n \times 1} , \ \mathbf{b}\in\R^{n\times 1}$ ，以及 $(\mathbf{a}\mathbf{b})^T = \mathbf{b}^T\mathbf{a}^T$，从上式我们可以得到我们的优化目标就是通过学习得到一个旋转矩阵 $\mathbf{R}^i$ 使得 $\eta^{i} \cdot \operatorname{tr}\left(\mathbf{b}_{w^{\prime}}^{i}\left(\mathbf{w}^{i}\right)^{T} \mathbf{R}^{i}\right)$ 尽量大。但是，直接学习一个旋转矩阵 $\mathbf{R}^i\in\R^{n^i\times n^i}$ 太大了，可能会给神经网络增加百万个参数，这在空间和时间上都打到了 $O\left(\left(n^{i}\right)^{2}\right)$ 的复杂度。

为了解决这个问题，受到Kroneckr product 克罗内克内积的启发，提出了一个 bi-rotation 方案，使用两个更小的旋转矩阵 $\mathbf{R}_{1}^{i} \in \mathbb{R}^{n_{1}^{i} \times n_{1}^{i}} \text { and } \mathbf{R}_{2}^{i} \in \mathbb{R}^{n_{2}^{i} \times n_{2}^{i}}$，来重构大的旋转矩阵 $\mathbf{R}^i\in\R^{n^i\times n^i}$ ，其中 $n^i=n^i_1\times n_2^i$ ，克罗内克内积的一个基本性质是如果两个矩阵 $\mathbf{R}_{1}^{i} \in \mathbb{R}^{n_{1}^{i} \times n_{1}^{i}} \text { and } \mathbf{R}_{2}^{i} \in \mathbb{R}^{n_{2}^{i} \times n_{2}^{i}}$ 是正交的，那么他们的克罗内可内积 $\mathbf{R}_{1}^{i} \otimes \mathbf{R}_{2}^{i} \in \mathbb{R}^{n_{1}^{i} n_{2}^{i} \times n_{1}^{i} n_{2}^{i}}$ 也是正交的。另外一个性质是：

其中的 $\text{Vec}(\cdot)$ 表示将其输入进行向量化，$\text{Vec}(\mathbf{W}^i) = \mathbf{w}^i$ ，因此对 $\mathbf{W}^i$ 应用 bi-rotation 等价于对 $\mathbf{w}^i$ 使用 $\mathbf{R}^{i}=\mathbf{R}_{1}^{i} \otimes \mathbf{R}_{2}^{i} \in \mathbb{R}_{1}^{n_{1}^{i} n_{2}^{i} \times n_{1}^{i} n_{2}^{i}}$ 进行旋转。所以，学习两个较小的矩阵，可以很好地重构一个大的旋转矩阵。此外，使用bi-rotation只会消耗 $O((n^i_1)^2+(n_2^i)^2)$ 的空间复杂度，以及 $O((n^i_1)^2n_2^i+n_1^i(n_2^i)^2)$ 的时间复杂度（这里存疑）。所以，可以得到下式（如何推导存疑），其中 $\mathbf{B}_{W^{\prime}}^{i}=\operatorname{sign}\left(\left(\mathbf{R}_{1}^{i}\right)^{T} \mathbf{W}^{i} \mathbf{R}_{2}^{i}\right)$：

最终，我们可以得到我们的优化目标：

2.3 Alternating Optimization

由于优化目标对于 $\mathbf{B}_{W^{\prime}}^{i}, \mathbf{R}_{1}^{i} \text { and } \mathbf{R}_{2}^{i}$ 是非凸（non-convex）的，所以为了找到一个可行的解决方法，我们采用了一个交替优化（alternating optimization）的方案，也就是说，更新一个变量的时候，固定住剩余两个变量的值，交替进行直到收敛。具体如下：

1）$\mathbf{B}_{W^{\prime}}^{i}$ -step：

固定 $\mathbf{R}^i_1$ 和 $\mathbf{R}^i_2$ 然后学习$\mathbf{B}^i_{W^\prime}$ ，那么优化目标就变成了：

由于 $\mathbf{B}_{W^{\prime}}^{i^{\prime}}=\operatorname{sign}\left(\left(\mathbf{R}_{1}^{i}\right)^{T} \mathbf{W}^{i} \mathbf{R}_{2}^{i}\right)$，所以这是一个定值。

2）$\mathbf{R}^i_{1}$ -step：

固定 $\mathbf{B}^i_{W^\prime}$ 和 $\mathbf{R}^i_2$ 然后更新$\mathbf{R}^i_1$ ，那么优化目标就变成了：

其中，$\mathbf{G}_{1}^{i}=\mathbf{B}_{W^{\prime}}^{i}\left(\mathbf{R}_{2}^{i}\right)^{T}\left(\mathbf{W}^{i}\right)^{T}$,上式的最大值可以用 polar decomposition 极分解来得到（推导过程存疑）：$\mathbf{R}_{1}^{i}=\mathbf{V}_{1}^{i}\left(\mathbf{U}_{1}^{i}\right)^{T}$，其中 $\mathbf{G}_{1}^{i}=\mathbf{U}_{1}^{i} \mathbf{S}_{1}^{i}\left(\mathbf{V}_{1}^{i}\right)^{T}$ 是$\mathbf{G}^i_1$ 的SVD。

3）$\mathbf{R}_{2}^{i}$ -step：

固定 $\mathbf{B}^i_{W^\prime}$ 和 $\mathbf{R}^i_1$ 然后更新$\mathbf{R}^i_2$ ，那么优化目标就变成了：

其中，$\mathbf{G}_{2}^{i}=(\mathbf{W}^{i})^T\mathbf{R}_{1}^{i}\mathbf{B}^i_{W^\prime}$,上式的最大值可以用 polar decomposition 极分解来得到：$\mathbf{R}_{2}^{i}=\mathbf{U}_{2}^{i}(\mathbf{V}_{2}^{i})^{T}$，其中 $\mathbf{G}_{2}^{i}=\mathbf{U}_{2}^{i} \mathbf{S}_{2}^{i}\left(\mathbf{V}_{2}^{i}\right)^{T}$ 是$\mathbf{G}^i_2$ 的SVD。

在实验中，交替更新三个变量，在三个循环后就可以达到收敛，因此，是非常高效的一种实现方式。

3.4 Adjustable Rotated Weight Vector

使用旋转矩阵对权重向量进行旋转调整后可以缩小权重向量二值化前后的角度偏差，我们可以令旋转后的权重向量为 $\tilde{\mathbf{w}}^{i}=\left(\mathbf{R}^{i}\right)^{T} \mathbf{w}^{i}$，接着会使用 sign 函数进行二值化，然后进行标准的梯度更新。不过，由于我们采用的是交替更新的策略，在更新的过程中很可能会陷入一个局部最优解，其在几何空间上的表示可以想象成，权重向量要么旋转过头了，要么旋转少了，为了解决这个问题，论文中提出了一个自调整的策略，其中 $\alpha^{i}=\operatorname{abs}\left(\sin \left(\beta^{i}\right)\right) \in[0,1] \text { and } \beta^{i} \in \mathbb{R}$：

如下图所示，其中绿色向量表示原权重向量的位置，黄色向量表示旋转后的位置，蓝色表示权重向量二值化后的位置，紫色为引入自调整策略后旋转后的向量的位置。图a表示转过头的情况，此时 $\alpha^i\le1$ ，使得其可以回调到紫色位置，图b表示没转够的情况，此时 $\alpha^i\ge1$ ，使其可以调整到紫色位置。图c是一个在ResNet20中训练的小样本的 $\alpha^i$ 随着epoch的变化，可以发现都处于 $\alpha^i\le1$ 的情况，所以可以得知转过头的情况占主导地位，所以限制为 $\alpha^i\in[0,1]$。

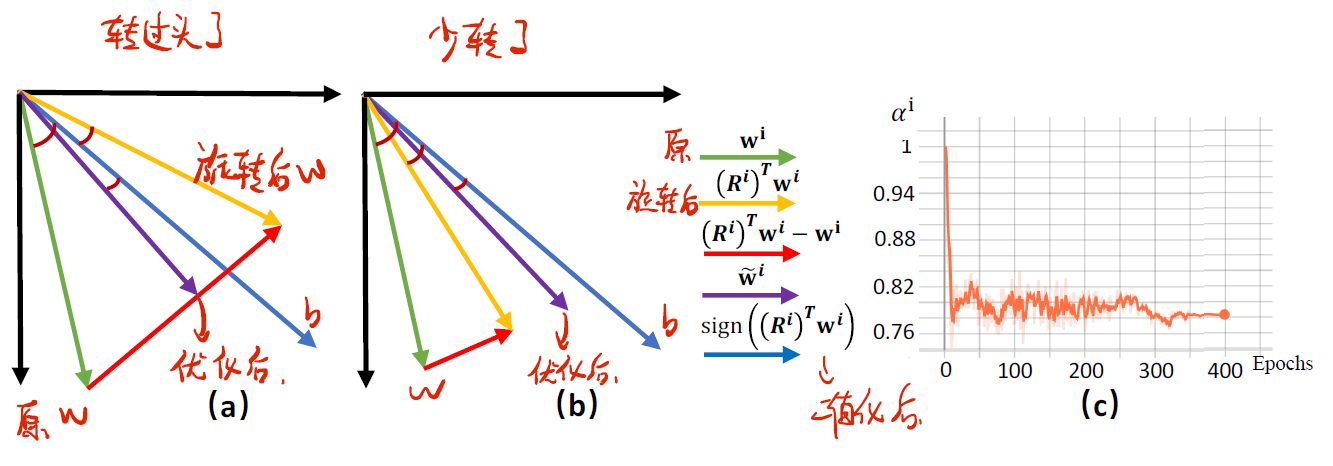
总的来说，在每个训练epoch的一开始，我们固定 $\mathbf{w}^i$ 来学习旋转矩阵，然后在训练阶段，我们固定旋转矩阵，对权重 $\mathbf{w}^i$ 进行旋转得到 $\tilde{\mathbf{w}}^{i}$（使用自调整策略），然后对 $\mathbf{w}^i$ 和 $\beta^i$ 进行更新。

3.5 Gradient Approximation

由于 sign 函数的导数几乎处处为0，这就使得训练变得很困难，为了解决这个问题，文献中提出了各种梯度近似方法，以实现梯度更新，比如说straight through estimation , piecewise polynomial function , annealing hyperbolic tangent function , error decay estimator 等，本文提出了一个 training-aware 的近似函数来代替sign函数：

其中 $t=10^{T_{\min }+\frac{e}{E} \cdot\left(T_{\max }-T_{\min }\right)}, \quad k=\max \left(\frac{1}{t}, 1\right),T_{\min }=-2, T_{\max }=1$，$E$ 表示训练的总epoch次数，$e$ 表示当前的epoch，所以可知， $F(x)$ 的图像由 $\frac e E$ 决定，即训练的进度。$F(x)$ 关于输入的导数如下：

$F(x)$ 及其导数的图像如下图所示，其中28%表示训练的进度为28%，以此类推。

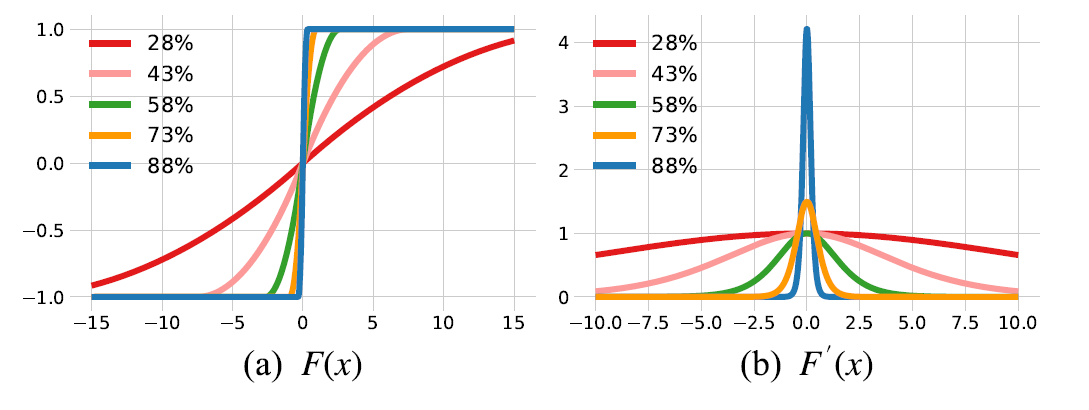
可以看到，在训练的一开始几乎处处都存在梯度，这可以克服sign的缺陷，使得整个网络都可以进行更新。而随着训练的进行，函数图像逐渐近似 sign 函数，这可以保证二值化的特性。因此，这样的近似函数是 train-aware，即可以感知训练进度的。到此，我们就可以写出损失函数关于激活值和权值的梯度：

其中：

此外， $\alpha^i$ 的梯度也可以计算：

其中，$[\cdot]_j$ 表示输入向量的第 $j$ 个元素。

3. Experiments

对RBNN在多个网络和多个数据集中进行了验证，实现过程中，除了第一层和最后一层，所有的卷积层和全连接层都进行了二值化，并使用SGD作为优化器。

3.1 Experimental Results

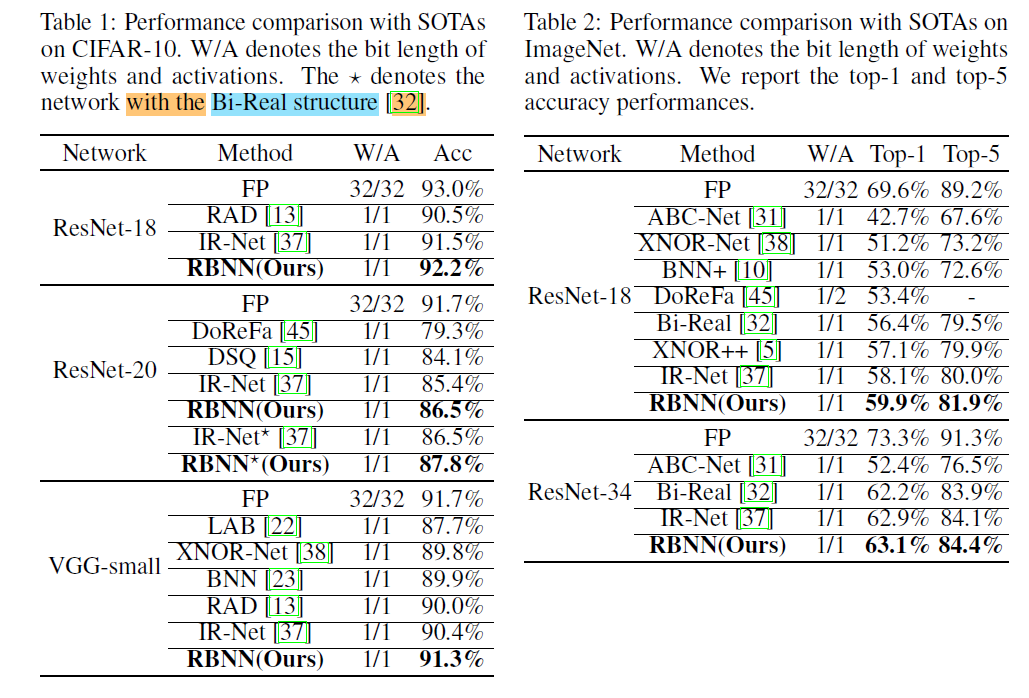
3.2 Performance Study

上一节展示了RBNN与其他SOTA网络的精度对比，可以看出RBNN的效果很好。这一节主要研究不同部分对RBNN的影响。本节所有的实验都是在CIFAR-10数据集上，使用ResNet-20以及Bi-Real结构的RBNN作为网络模型。

下表展示了使用RBNN作为模型，采用不同的梯度近似函数，包括STE、PPF、EDE以及本文提到的近似函数。可以看出，本文提出的表现效果最好，这也验证了本文提出的近似函数的正确性。

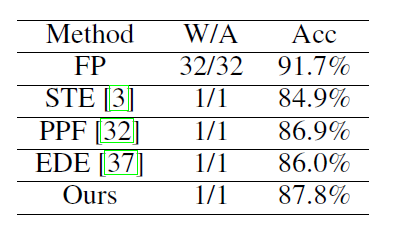
接着又进行了一次消融实验（ablation study），如下表所示，使用XNOR-Net作为网络模型（用B表示），然后再XNOR-Net中逐渐添加 权重旋转（R），training-aware 近似器（T），自调整策略（A），结果如下，可以证明，每一个部分都对精度的提升起到一定的作用。

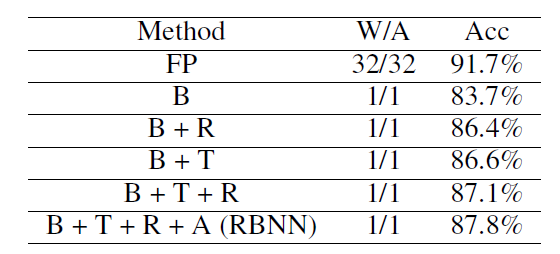
3.3 Weight Distribution and Flips

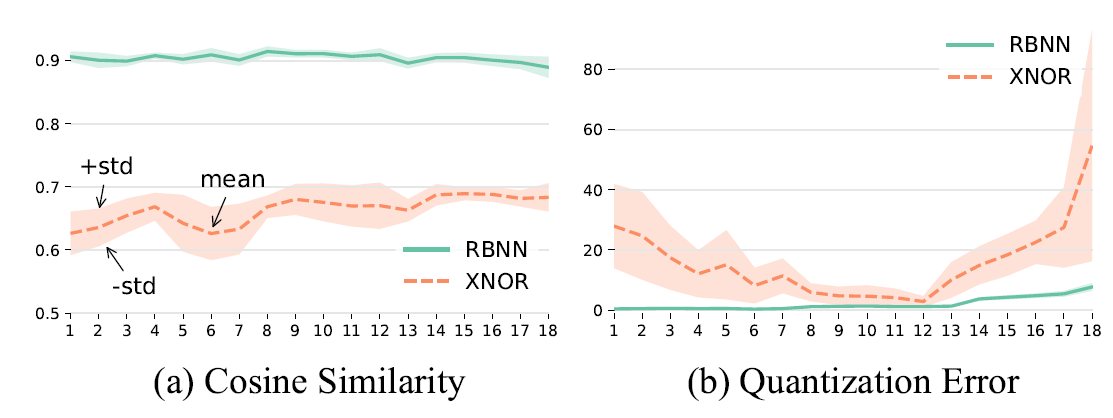
下图的直方图展示了训练后的XNOR网络和RBNN中权重在二值化之前的分布情况。我们可以看到，在XNOR中，权重在零点中心附近紧密地混合在一起，其值的大小仍然远远小于1，这样就很可能在二值化的时候造成误差，因为权重的值之间数值差距小且大部分为0，而在RBNN中，权重以0为分界点线，基本均匀分布在两侧，且值之间的差异较大.

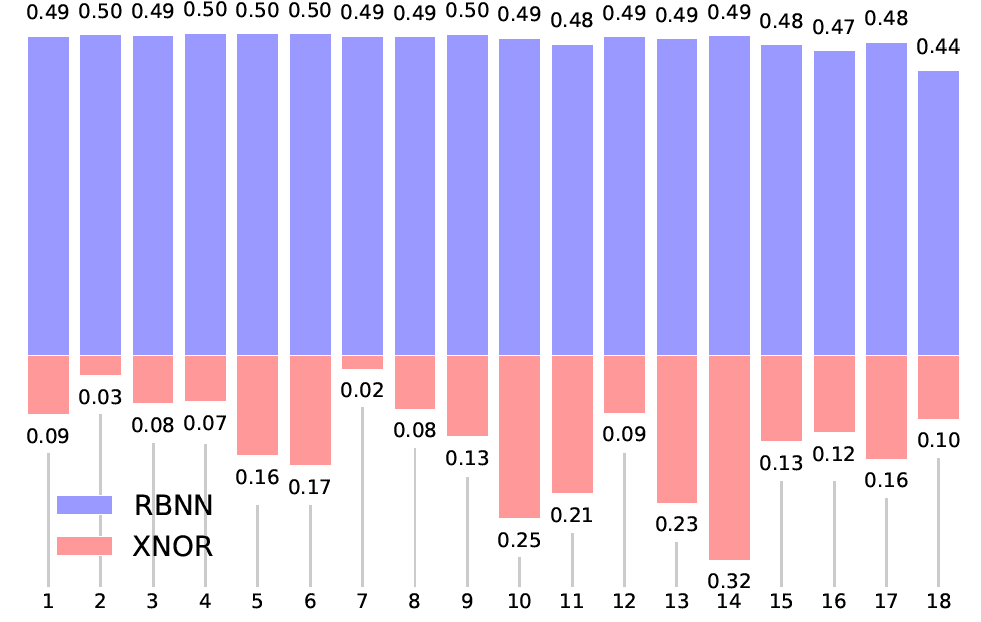
前面介绍过，当权重翻转的概率为50%的时候，BNN的学习能力达到最大。我们比较RBNN和XNOR-Net中在ResNet-20的每一层权重的翻转概率，如下所示，可以发现RBNN翻转的概率都在50%左右，而XNOR的翻转概率都普遍较低。这也说明了RBNN在训练时可以获得尽可能多的信息。

 

4. Conclusion

在本文中，分析了角度偏差对二元神经网络量化误差的影响，并提出了旋转二元神经网络（RBNN），以实现在每个训练epoch开始前旋转权重向量，使旋转后的向量与其二值化后的向量之间的角度对齐。我们还引入了一个涉及两个较小旋转矩阵的方案 bi-rotation，以减少学习大旋转矩阵的复杂度。在训练阶段，我们在反向传播的过程中，利用梯度来动态地调整旋转的权重向量，以克服bi-rotation优化中潜在的局部最优解的问题。我们的旋转通过实现大约50%的权重翻转，使学习BNN的信息增益最大化。为了实现梯度传播，我们设计了一个training-aware的函数来近似sign函数。大量的实验证明了我们的RBNN在减少量化误差方面的功效，以及它比几个SOTA的优势。

5. Broader Impact

优势：

二元神经网络的研究者可能从我们的研究中受益。所提出的旋转二元神经网络（RBNN）提供了一个新的视角，通过减少角度偏差来减少量化误差，这一点在以前的工作中被忽视。随着代码的公开，我们的工作也将帮助研究人员对DNN进行量化，从而使深度模型可以部署在资源有限的设备上，如手机。

劣势：

activation和其二值化之间的角度偏差仍然是一个待解决的问题，因为本论文中提出的RBNN不适合在激活值上，因为这会增加推理所需的计算资源。

结论：

网络量化的失败不会带来严重的后果，因为与其他SOTA相比，我们的RBNN造成的精度下降较少。

数据偏差：

提出的RBNN与数据选择无关，所以它不存在数据偏差问题。