CS231n第十二节：强化学习

本系列文章基于CS231n课程，记录自己的学习过程，所用视频资料为 2017年版CS231n，阅读材料为CS231n官网2022年春季课程相关材料

本节将介绍一些强化学习相关的内容。

1. 强化学习

1.1 定义

如下图所示，就是强化学习的工作过程。首先，存在一个环境，和一个代理，环境先给代理一个状态 $s_t$ ，然后代理根据这个状态输出一个动作 $a_t$ 给环境。环境接受这个动作后进行评估，反馈给代理一个奖励值 $r_t$ ，以及下一步状态 $s_{t+1}$ ，如此往复直到环境给出一个终结状态。这样一个模型的目标是尽可能地获得更多的奖励值。

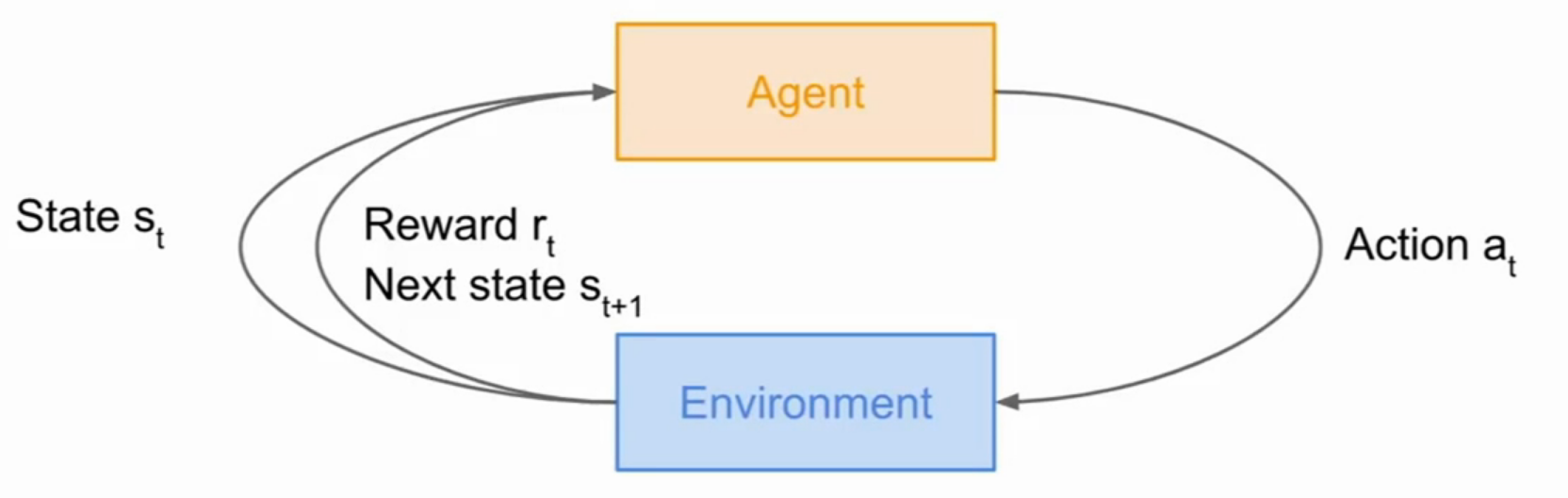
1.2 应用

强化学习有很多的应用，举几个比较常见的例子：

小车平衡问题

目标：平衡正在移动的小车上的杆使其处于上方。

状态：杆与水平线的角度，杆运动的角速度，小车位置，小车水平速度。

动作：给小车施加横向的力。

奖励：每一时刻，如果杆位于小车正上方，则得1分。

机器人移动问题

目标：让机器人学会自己向前移动

状态：关节的角度和位置

动作：施加在关节上的力矩

奖励：每一时刻如果机器人向右前方前进，则得1分

街机游戏

目标：在游戏中获得更高的分数

状态：当前游戏的元素像素值

动作：游戏中的控制，比如前后左右

奖励：由每一时刻游戏得分的升降决定

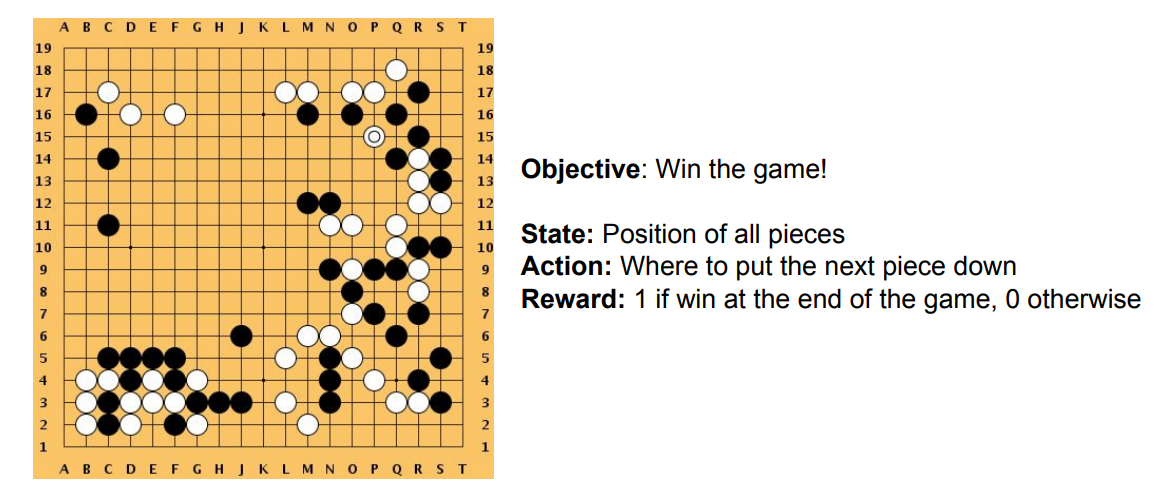
围棋

目标：获得游戏的胜利

状态：每个棋子的位置

动作：下一步应该下在什么位置

奖励：如果最终游戏胜利则得1分，否则0分

2. 马尔科夫决策过程

2.1 定义

马尔科夫决策过程就是强化学习的数学公式化，其符合马尔科夫性质——当前的状态可以完全地描述世界的状态。

马尔科夫决策过程由一个包含五个元素的元组构成：$(\mathcal{S}, \mathcal{A}, \mathcal{R}, \mathbb{P}, \gamma)$，每个元素的含义如下：

• $\mathcal{S}$：表示所有可能的状态的集合。
• $\mathcal{A}$：表示所有可能的动作的集合。
• $\mathcal{R}$：表示给定一对（状态，动作）的奖励值的分布，即一个从（状态，动作）到奖励值的映射。
• $\mathbb{P}$：状态转移概率，即给定一对（状态，动作）时下一个状态的分布。
• $\gamma$：折扣因子，即对近期奖励和长远奖励之间的一个权重。

2.2 工作方式

• 首先在初始阶段 $t=0$ 时，环境会从初始状态分布 $p(s_0)$ 中进行采样，得到初始状态，即 $s_0\sim p(s_0)$

• 然后，从 $t=0$ 开始一直到整个过程结束，重复下述过程：

  • 代理根据当前状态 $s_t$ 选择一个动作 $a_t$
  • 环境采样得到一个奖励值 $r_t \sim R(.|s_t,a_t)$
  • 环境采样得到下一个状态 $s_{t+1}\sim P(.|s_t,a_t)$
  • 代理接受到奖励值 $r_t$ 和下一个状态 $s_{t+1}$

其中，定义一个策略 $\pi$ 表示一个从 $S$ 到 $A$ 的函数，用于指明在每个状态下应该采取哪个动作。所以，目标就是寻找到一个策略 $\pi^*$ 使得累加的折扣奖励值（即使用 $\gamma$ 加权后的奖励值） $\sum_{t>0} \gamma^{t} r_{t}$ 最大。下面举一个简单的例子：

如下图的网格中，我们的状态就是这样一个网格和当前所在的位置，动作的集合为上下左右移动，每进行一次移动就会得到一个-1的奖励值。我们的目标是采取最少的步数，到达任意一个终点（星标格子）。如下图所示就是两个不同的策略，即 $\pi$ 函数，其中左边就是完全随机策略，右边则是一个最优的策略。

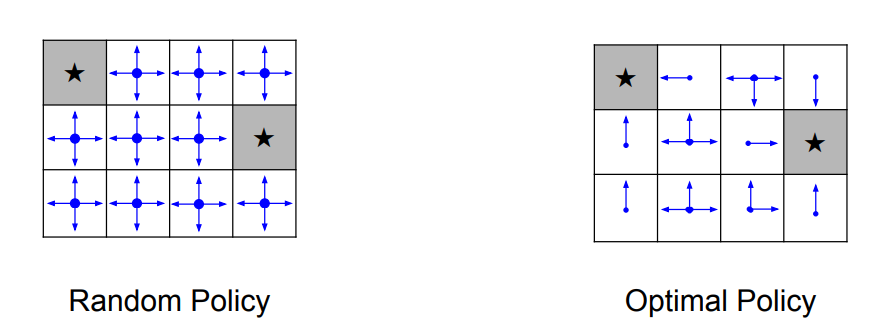
那么，我们如何寻找这样一个最优的策略 $\pi ^*$ ，使得最大化奖励值的总和呢？首先，我们可以给出 $\pi$ 的正式表达式：

3. Q-learning

3.1 一些定义

价值函数

对于一个给定的策略 $\pi$ ，我们只要给定初始状态 $s_0$ ，那么就可以依次产生一个序列 $s_0,a_0,r_0,s_1,a_1,r_1...$

也就是说，给定一个策略 $\pi$ 后我们就能计算出在状态 $s$ 下能产生的累积奖励值的期望，这就是价值函数：

注意，价值函数评价了给定策略 $\pi$ 下状态 $s$ 的价值，由策略 $\pi$ 和当前状态 $s$ 所唯一确定。

Q-价值函数 Q-value

Q-价值函数则评价了给定策略 $\pi$ 下，在状态 $s$ 下采取动作 $a$ 后，所能带来的累积奖励期望：

Q-价值函数由策略 $\pi$ 和当前状态 $s$ 和当前动作 $a$ 所唯一确定。

贝尔曼方程 Bellman equation

现在我们固定当前状态 $s$ 和当前动作 $a$，那么目标就是要选择最优策略 $\pi$，使得Q-value函数最大，这个最优的Q-value函数被记为$Q^*$：

理解一下 $Q^*$，也就是在当前状态 $s$ 下采取动作 $a$ 后，所能达到的最大累积奖励期望。显然 $Q^*$ 仅与 $s$ 和 $a$ 有关。而强化学习方法 Q-learning 的核心公式——贝尔曼方程，则给出了$Q^*$的另一种表达形式：

理解：当我们在状态 $s$ 下采取动作 $a$ 后，环境会反馈给我们一个奖励 $r$ ，以及下一时刻可以转移的状态 $s'$（一个集合），以及对应的动作 $a'$，我们选择状态集合中Q-value最大的作为转移状态，即 $Q^{*}(s^{\prime}, a^{\prime})$ 最大，也就是说我们每次转移都选取期望奖励最大的作为下一次的状态，这样我们就可以递归地调用 $Q^*$ 了。

3.2 Value iteration 算法

Bellman方程中使用 Q-value 给每次的一个情况（即一个特定的状态和动作组合）都指示了接下来转移的状态和动作，那么只要求得 所有的 Q-value ，就能找到最优策略 $\pi^*$。

一个最简单的思路就是将贝尔曼方程看成一个迭代更新的式子：

即新的Q-value由旧的Q-value得到，初始时所有的Q-value为0。

具体例子可以参考：https://blog.csdn.net/itplus/article/details/9361915

那么只要迭代足够多的次数，就能得到所有的Q-value值，但是这有个问题，就是这个方法的拓展性很差。由于要求出所有的Q-value，那么对于一些任务，比如自动玩游戏，其状态为所有的像素，这样庞大的计算几乎是不可能实现的。

3.3 神经网络求Q-value

因此，我们需要使用一个函数估计器去逼近真实的Q-value，通常神经网络是一个很好的函数估计器，即：

其中的 $\theta$ 表示神经网络的参数，使用这样一个式子，神经网络可以自学习调整 $\theta$ 使得其在给定的 $s$ 和 $a$ 下输出值约等于 $Q^*$ ，要使用神经网络训练就需要规定损失函数，由于这是一个回归问题，所以很自然地我们就能想到使用L2损失函数：

其中，$y_i$ 表示真实值：

于是，在反向传播是我们计算梯度：

下面我们以前面提到的街机游戏作为一个例子说明，首先回顾一下街机游戏的目标：

• 目标：在游戏中获得更高的分数

• 状态：当前游戏的元素像素值

• 动作：游戏中的控制，比如前后左右

• 奖励：由每一时刻游戏得分的升降决定

我们有如下一个网络结构，将最近的4帧游戏图片进行灰度化以及一些下采样等预处理后得到 $84*84*4$ 的一个输入，然后通过两个卷积层提取特征，最后使用两个全连接层输出一个 $4$ 维向量，表示输入状态下，分别为上下左右四个动作时的 Q-value，于是我们就可以训练这个网络了。

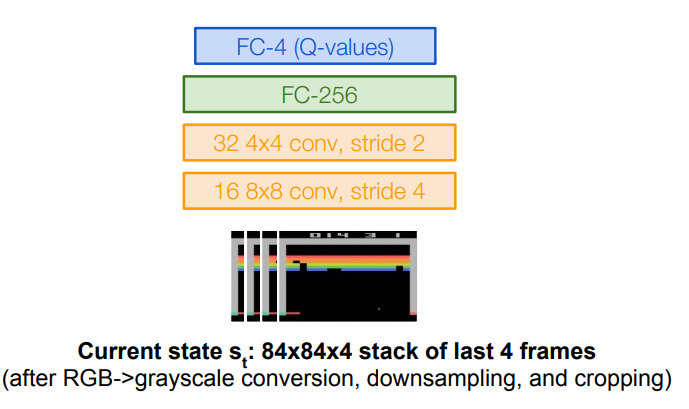
3.4 Experience Replay

但是直接训练有个问题：数据相关性。在使用神经网络逼近函数的方法里，我们修改的是参数 $θ$，因为函数通常是连续的，所以为了调整参数使得 $Q(s,a)$ 更加接近真实值，也会修改 $s$ 附近的其它状态。比如我们调整参数之后 $Q(s,a)$ 变大了，那么如果 $s’$ 很接近 $s$，那么 $Q(s’,a)$ 也会变大。比如在上面的游戏中，状态 $s$ 可以表示为连续 4 帧的图像，两个连续状态肯定很像(可能就是几个像素的区别)，而我们更新的target又依赖于 $\max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_{i-1}\right)$，因此这会起到一种放大作用，使得所有估计都偏大，这就很容易造成训练的不稳定。于是，提出了 Experience replay 来解决这个问题。

为了避免数据的相关性，它会有一个replay buffer，用来存储近期的一些 $(s,a,r,s’)$ 。训练的时候随机的从replay buffer里均匀的采样一个 minibatch 的 $(s,a,r,s’)$ 来调整参数 $θ$。因为是随机挑选的，所以这些数据不太可能有前后相关性。当然，这种方法也有弊端，就是训练的时候是 offline 的形式，无法做到 online 的形式。

3.5 算法流程

上面算法流程图中的过程其实就是在训练一个深度神经网络，因为神经网络是被证明有万有逼近的能力的，也就是能够拟合任意一个函数；一个 episode 相当于 一个 epoch。

4. Policy Gradients

4.1 定义

上面介绍的Q-learning有个问题就是 $Q$ 函数可能会非常复杂，比如说控制机器人抓取物体就是一个高维的状态，所以对于提取每一对 （状态，动作）对应的价值就十分困难了。但是，其实这样一个目标的策略是十分简单的——只要控制机器人的手握紧就行。所以，我们是否可以直接去学习策略，即从一堆策略集合中选择一个最佳的策略，而不是使用间接的方式。首先，我们将策略进行参数化：

然后对于每个给定的参数化策略，定义其价值函数：

所以，我们的目标就变成了找到一个 $\theta^{*}=\arg \max _{\theta} J(\theta)$，实现方法就是对策略参数进行梯度上升。

4.2 REINFORCE algorithm

在数学上，我们可以将上文的价值函数换一种写法：

其中的 $r(\tau)$ 表示一个行动轨迹的价值， $\tau=\left(s_{0}, a_{0}, r_{0}, s_{1}, \ldots\right)$，也就是说现在我们只需要求出梯度 $\nabla_{\theta} J(\theta)=\int_{\tau} r(\tau) \nabla_{\theta} p(\tau ; \theta) \mathrm{d} \tau$ 然后使用梯度上升更新参数即可。可是，问题是这个梯度是不好求的，因为这里的 $p$ 依赖于 $\theta$。不过，我们可以使用一个很好的技巧，将梯度转换成：

于是就有：

我们就可以得到下面这样的结论：

对于这样一个策略价值的梯度，有这样的解释：

• 如果 $r(\tau)$ 很高，那么我们就提高我们所看见的动作的概率

• 如果 $r(\tau)$ 很高，那么我们就降低我们所看见的动作的概率

   

4.3 Variance reduction

一些方法

使用Baseline

一个简单的基准就是使用目前为止，所有轨迹所经历的奖励的恒定移动平均值，即：

一个更好的基准就是从一个状态中推高一个行动的概率，如果这个行动比我们应该从该状态中得到的预期值更好。

4.4 Actor-Critic Algorithm

4.5 Recurrent Attention Model

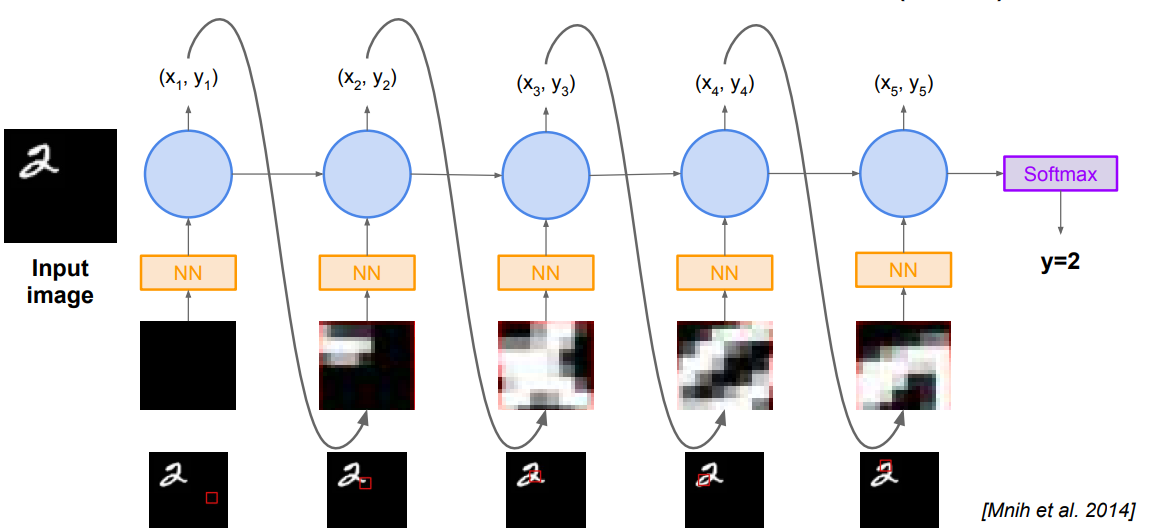
4.6 AlphaGo