熟能生巧：深度解析 Pi0.6* 强化学习新范式——RECAP

关键词：具身智能 (Embodied AI) $\cdot$ VLA 模型 $\cdot$ 离线强化学习 (Offline RL) $\cdot$ 优势条件化 (Advantage Conditioning)

1. 引言

当前的视觉-语言-动作（Vision-Language-Action, VLA）模型，如 $\pi_{0}$，虽然展现出了惊人的多任务通用能力，但其核心训练范式依然停留在 模仿学习（Imitation Learning, IL） 阶段。这使得机器人的表现存在一个明显的上限：虽然能通过人类示教数据学会基本操作，但由于缺乏自我试错和反馈修正机制，一旦遇到未曾见过的情况（OOD），模型往往束手无策，且永远无法超越示教者的水平。为了让机器人实现从“模仿”到“精通”的跨越，引入 强化学习（RL） 是必然选择。

然而，将传统的在线 RL 算法（如 PPO）直接套用到拥有数十亿参数的 VLA 模型上面临巨大挑战：

Instantiating these principles in a general and scalable robotic learning system presents significant challenges: designing scalable and stable RL methods for large models, handling heterogeneous data from different policies, and setting up RL training with reward feedback in the real world, where rewardsignals might be ambiguous or stochastic.

核心痛点在于：

训练不稳定性：在大模型上进行自举（Bootstrapping）更新极易触发 RL 领域的“训练发散”问题（即 Deadly Triad），难以扩展。
数据异质性：难以统一处理来自不同策略（人类演示、旧策略、新策略）的异质数据。
奖励噪声：真实世界的 Reward 往往模糊不清且充满随机噪声。

本文将深入解读 RECAP (RL with Experience and Corrections via Advantage-conditioned Policies)。这项工作并没有简单地堆砌 RL 技巧，而是从理论底层重构了策略提取方式，通过 “优势条件化” 将复杂的 RL 问题转化为条件监督学习。它在保证大模型训练绝对稳定性的前提下，利用自主回放和人类修正数据，让 VLA 在真实世界任务中实现了性能翻倍。

2. 理论重构：从“数值加权”到“条件生成”

RECAP 的系统框架流程清晰（如图所示）：

利用海量数据预训练一个通用的 VLA 模型 $\pi_{\text{pre}}$（即 $\pi_{0.6}$）。
利用机器人数据预训练一个 Value Function 模型（架构为缩小版 VLA）。
针对下游任务进行 SFT 后，模型在现实世界中执行任务并收集数据（包含自主成功/失败数据及人类纠正数据）。
利用收集的数据微调 Value Function。
利用 Value Function 计算 Advantage 并作为 Condition，迭代微调 Policy，最终得到 $\pi_{0.6}^*$。

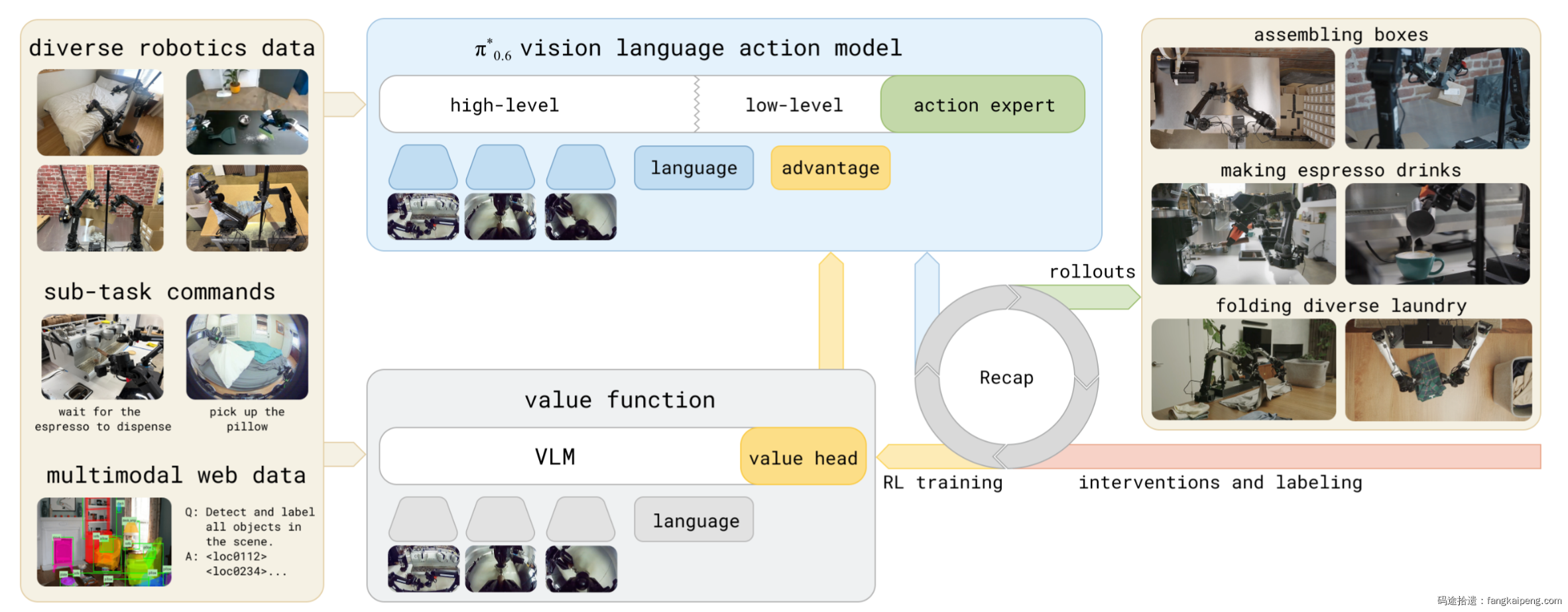
值得注意的是，将 Advantage 作为 Condition 加入 VLA 输入并非单纯的经验主义尝试，而是从强化学习正则化理论一步步严密推导而来的。

2.1 经典困境：指数加权的局限性

在正则化 RL 中，我们的目标是在最大化奖励的同时，通过 KL 散度或其他衡量分布差异的metric来约束新策略 $\pi$ 不偏离参考策略 $\pi_{\text{ref}}$：

$$
\mathcal{J}(\pi, \pi_{\text{ref}}) = \mathbb{E}_{\tau \sim \rho_\pi} [\sum \gamma^t r_t] – \beta \mathbb{E}_{o \sim \rho_\pi} [D_{\text{KL}}(\pi(\cdot|o) || \pi_{\text{ref}}(\cdot|o))]
$$

公式的前半段表示期望累积回报，后半段表示两个policy之间的分布差异，针对此目标的经典闭式解（如 Advantage Weighted Regression 算法）为：

$$
\hat{\pi}(\mathbf{a}|\mathbf{o}) \propto \pi_{\text{ref}}(\mathbf{a}|\mathbf{o}) \exp\left(\frac{A^{\pi_{\text{ref}}}(\mathbf{o}, \mathbf{a})}{\beta}\right)
$$

$A$ 表示优势Advantage，其定义为（N-step Advantage Estimate）：

$$
A^\pi(\mathbf{o}_t, \mathbf{a}_t) = \underbrace{\mathbb{E}_{\rho_\pi(\tau)} \left[ \sum_{t'=t}^{t+N-1} r_{t'} + V^\pi(\mathbf{o}_{t+N}) \right]}_{\text{动作价值估计 (类似于 } Q(\mathbf{o}_t, \mathbf{a}_t))} – \underbrace{V^\pi(\mathbf{o}_t)}_{\text{平均回报}}
$$

简单可以理解成：

$$
\text{优势} = (\text{采取动作 } \mathbf{a}_t \text{ 后的评估回报}) – (\text{在该状态下的平均回报})
$$

因此：

如果 $A > 0$：说明动作 $\mathbf{a}_t$ 比平均水平好，我们应该鼓励（增加其概率）。

如果 $A < 0$：说明动作 $\mathbf{a}_t$ 比平均水平差，我们应该抑制（减小其概率）。

这种方法本质上是一种 “加权回归”：优势 $A$ 越大的动作，权重呈指数级放大，举例：

情况 A：动作很棒 (Advantage > 0)

假设 $A = 2$。$$\exp(2) \approx 7.39$$，这意味着，新策略 $\hat{\pi}$ 选择这个动作的概率，应该是旧策略的 7 倍多。

结果：好动作被强烈鼓励。

情况 B：动作很差 (Advantage < 0)

假设 $A = -2$。$$\exp(-2) \approx 0.135$$，这意味着，新策略 $\hat{\pi}$ 选择这个动作的概率，应该只有旧策略的 13%。

结果：坏动作被强烈抑制。

情况 C：动作平平无奇 (Advantage ≈ 0)

$$\exp(0) = 1$$。新策略的概率 $\approx$ 旧策略的概率。

结果：保持现状。

2.2 范式转换：引入改进概率 $I$

RECAP 引用了一个较新的理论结果，将关注点从“优势的具体数值”转移到了 “该动作能带来改进的概率” 上，最优策略的形式重构为：

$$
\hat{\pi}(\mathbf{a}|\mathbf{o}) \propto \pi_{\text{ref}}(\mathbf{a}|\mathbf{o}) \cdot \underbrace{p(I | A^{\pi_{\text{ref}}}(\mathbf{o}, \mathbf{a}))^\beta}_{\text{动作a可以带来改进的概率}}
$$

在前一个“经典解法”中，我们把优势 $A$ 看作一个连续的分数。

公式：$\hat{\pi} \propto \pi_{\text{ref}} \cdot \exp(A/\beta)$

逻辑：

如果这个动作 $A=10$（分很高），我就用 $\exp(10)$ 这个巨大的倍数去放大它的概率。

如果这个动作 $A=-10$（分很低），我就用 $\exp(-10)$ 这个微小的倍数去缩小它的概率。

问题：这像是一个“暴力”的数值加权。$\exp$ 函数很敏感，是一个无上界的数值（可以是 10000，也可以是 0.0001），分数值稍微波动一点，权重可能就会爆炸或者消失，计算上不够稳定。为了数值稳定，虽然可以把权重归一化到[0,1]的区间，但同样还有一个无法解决的问题：高分样本权重为 1（重点学），低分样本权重接近 0（直接忽略）。这导致模型实际上是在做“过滤后的模仿”，丢弃了关于“什么是错误动作”的宝贵信息。

现在：乘以 $p(I|A)$。这是一个有界的概率值（永远在 0 到 1 之间）。于是在理论上把“寻找最优策略”的问题，从“根据分数调整权重”变成了“寻找那些大概率能带来改进（$I$）的动作。也可以理解为把一个“回归问题”（预测优势具体是几分）转化为了一个更接近“分类问题”（预测这是不是一个好动作）的形式。直觉来讲，更加好学了，更加稳定了，不过仍然没有实现“利用错误信息”的需求，这是通过后面的Condition实现的。

但是，直接获取 $p(I|A)$ 这个概率模型比较困难，本文利用贝叶斯公式 进行了一次巧妙的反转：

$$
p(I | \mathbf{a}, \mathbf{o}) \propto \frac{\pi_{\text{ref}}(\mathbf{a} | I, \mathbf{o})}{\pi_{\text{ref}}(\mathbf{a} | \mathbf{o})}
$$

代入原式，我们得到了一个极其直观的最优策略公式：

$$
\tilde{\pi}(\mathbf{a}|\mathbf{o}, l) \propto \pi_{\text{ref}}(\mathbf{a}|\mathbf{o}, l) \left( \frac{\pi_{\text{ref}}(\mathbf{a}|I, \mathbf{o}, l)}{\pi_{\text{ref}}(\mathbf{a}|\mathbf{o}, l)} \right)^\beta
$$

我们两边取对数（Log），乘法变加法，除法变减法：

$$
\log \tilde{\pi} = \underbrace{\log \pi_{\text{ref}}(\mathbf{a}|\mathbf{o})}_{\text{A: 无条件基础策略}} + \beta \left( \underbrace{\log \pi_{\text{ref}}(\mathbf{a} | I, \mathbf{o})}_{\text{B: 有条件改进策略}} – \underbrace{\log \pi_{\text{ref}}(\mathbf{a} | \mathbf{o})}_{\text{A: 无条件基础策略}} \right)
$$

这个公式告诉我们，想要得到最优策略 $\tilde{\pi}$，我们不需要去算复杂的指数，只需要知道两个分布：

$\pi_{\text{ref}}(\mathbf{a}|\mathbf{o})$：无条件的参考策略（普通表现）。
$\pi_{\text{ref}}(\mathbf{a}|I, \mathbf{o})$：条件化的参考策略（即：在已知“必须改进”的前提下，你会怎么做？）。

为了不训练两个单独的网络，使用 Classifier-Free Guidance (CFG) 的训练技巧，用同一个网络 $\pi_{\theta}$ 来拟合这两个分布，通过同一个网络给定不同的输入（Prompt），得到两项损失构成最终的损失函数：

$$
\min_{\theta} \mathbb{E}_{\mathcal{D}_{\pi_{\text{ref}}}} \left[ \underbrace{-\log \pi_{\theta}(a_t|o_t, l)}_{\text{任务 1: 学通用分布}} \underbrace{- \alpha \log \pi_{\theta}(a_t|I_t, o_t, l)}_{\text{任务 2: 学条件分布}} \right]
$$

前一项的含义是：让模型在不看 Advantage 标签的情况下，尽可能复现数据集 $\mathcal{D}_{\pi_{\text{ref}}}$ 里的动作。

后一项的含义是：模型在看了 Advantage 标签（$I_t$）的情况下，尽可能准确地复现对应的动作，即同时学习好的动作是如何做的，以及坏的动作是如何做的。

3. 工程实现：在噪声中寻找确定性

理论推导虽然完美，但落地到充满噪声的机器人环境需要极高的鲁棒性。RECAP 在工程实现上做出了两个关键的“妥协”，正是这些设计保证了在大模型上训练的稳定性。

3.1 价值函数：回归本源的蒙特卡洛 (MC)

为了获取 Advantage，我们需要训练一个 Value Function ($V$)。值得注意的是，RECAP 没有使用数据效率更高的 Q-Learning（TD 方法），而是选择了被认为“效率较低”的 蒙特卡洛（Monte Carlo）估计器 。

$$
V^{\pi_{\text{ref}}}(o_t, l) = \mathbb{E}_{\text{dataset}} [\sum_{t'=t}^T r_{t'}]
$$

为什么放弃 Q-Learning？ Q-Learning 依赖“自举（Bootstrapping）”，即用下一步的预测更新当前的预测。在 VLA 这种巨型模型和离线数据（Off-policy）的结合下，极易触发强化学习中的“致命三要素（Deadly Triad）”，导致价值网络发散。

MC 的稳定性红利： MC 方法直接统计整条轨迹的真实回报总和。这是一种 On-policy Estimator（忠实评估产生数据的策略本身）。虽然方差较大（受全程随机性影响），但它是无偏且 绝对稳定 的——因为“事实”不会骗人，也不会发散。对于数十亿参数模型的微调，简单与可靠（Simple and Highly Reliable） 比微小的数据效率提升更重要。

此外，针对稀疏奖励问题，论文将 0/1 成功信号转化为“Time-to-Success”的密集奖励（每一步 -1），使 Value Function 能够衡量效率 :

$$
r(o_t, a_t) =
\begin{cases}
0 & \text{if } t=T \text{ and success} \\
T – C_{\text{fail}} & \text{if } t=T \text{ and failure} \\
-1 & \text{otherwise}
\end{cases}
$$

对于非终止的每一步给予 -1 的惩罚。这意味着成功时的总回报 $R = -\text{Steps}$，迫使模型寻找最快完成任务的路径（即最大化回报）。这一设计让 Value Function 的物理含义变成了预计距离成功的剩余步数。

3.2 策略条件化：二值化的智慧

在计算出 Advantage 后，RECAP 并没有将其直接作为连续数值输入，而是进行了 二值化（Binarization） 处理：

$A > \epsilon \Rightarrow$ Input: Advantage: positive
$A \le \epsilon \Rightarrow$ Input: Advantage: negative

Input vs. Weighting 的哲学选择：这是与 AWR 等方法最本质的区别。

Weighting (如 AWR)：试图通过 Loss 权重来抑制坏动作（Unlikelihood Training），梯度极其不稳定，且实际上是在丢弃负样本。
Conditioning (RECAP)：通过输入标签（Negative Prompt）让模型去 “理解” 坏动作。这使得模型能够利用失败数据学习环境动力学（World Model），即“我知道这样做会导致失败”。同时，二值化充当了一个强大的滤波器，过滤了 Advantage 估计中的高频噪声。

4. 算法流程：防漂移的“重置”循环

RECAP 的算法流程（Algorithm 1)展示了一个迭代提升的闭环。

Pre-train (Generalist)：在大规模多任务数据上训练通用的 $V_{\text{pre}}$ 和 $\pi_{\text{pre}}$ 。
Specialist Initialization (SFT)：收集少量目标任务数据 $\mathcal{D}_l$，微调得到专家模型 $\pi_{l}^0$ 。
Iterative Loop ：
- Collection：利用当前策略 $\pi_{l}^k$ 收集自主回放数据和人类修正数据。
- Update：重新训练 $V$ 和 $\pi$。

关键细节： 在第 $k$ 轮迭代中，模型并不是从第 $k-1$ 轮的权重继续训练，而是 重新加载预训练权重 ($\pi_{\text{pre}}$)，利用累积至今的所有数据 $\mathcal{D}_l$ 进行微调（Train from $V_{\text{pre}}$ / $\pi_{\text{pre}}$）。这一机制有效防止了 灾难性遗忘 和 策略漂移（Policy Drift），确保模型始终保有通用的物理常识，仅仅是在特定任务上进行“专精”。

5. 结语

RECAP 的成功证明了在机器人领域，“大模型 + 大算力 + 高稳定性”路线的可行性。虽然在价值估计上采用了较为保守的蒙特卡洛方法，牺牲了一定的数据效率，但这种 “以稳求进” 的策略，配合巧妙的 优势条件化 数学框架，让 VLA 模型真正具备了从经验中持续进化的能力。这项工作不仅提供了一个通用的微调框架，更向我们展示了如何利用那些通常被丢弃的“失败数据”，将其转化为通向精通之路的基石。