一、背包问题模型

背包问题（Knapsack problem）是一种组合优化的NP完全问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。常见的背包问题有：01背包，完全背包，多重背包，分组背包，混合背包，有依赖的背包问题等,考察方向一般为求最优解、最优方案数、最优方案。下面会分别介绍这几种背包问题的分析方法和例题。

本文所有例题均来自：Acwing 算法提高课

二、01背包

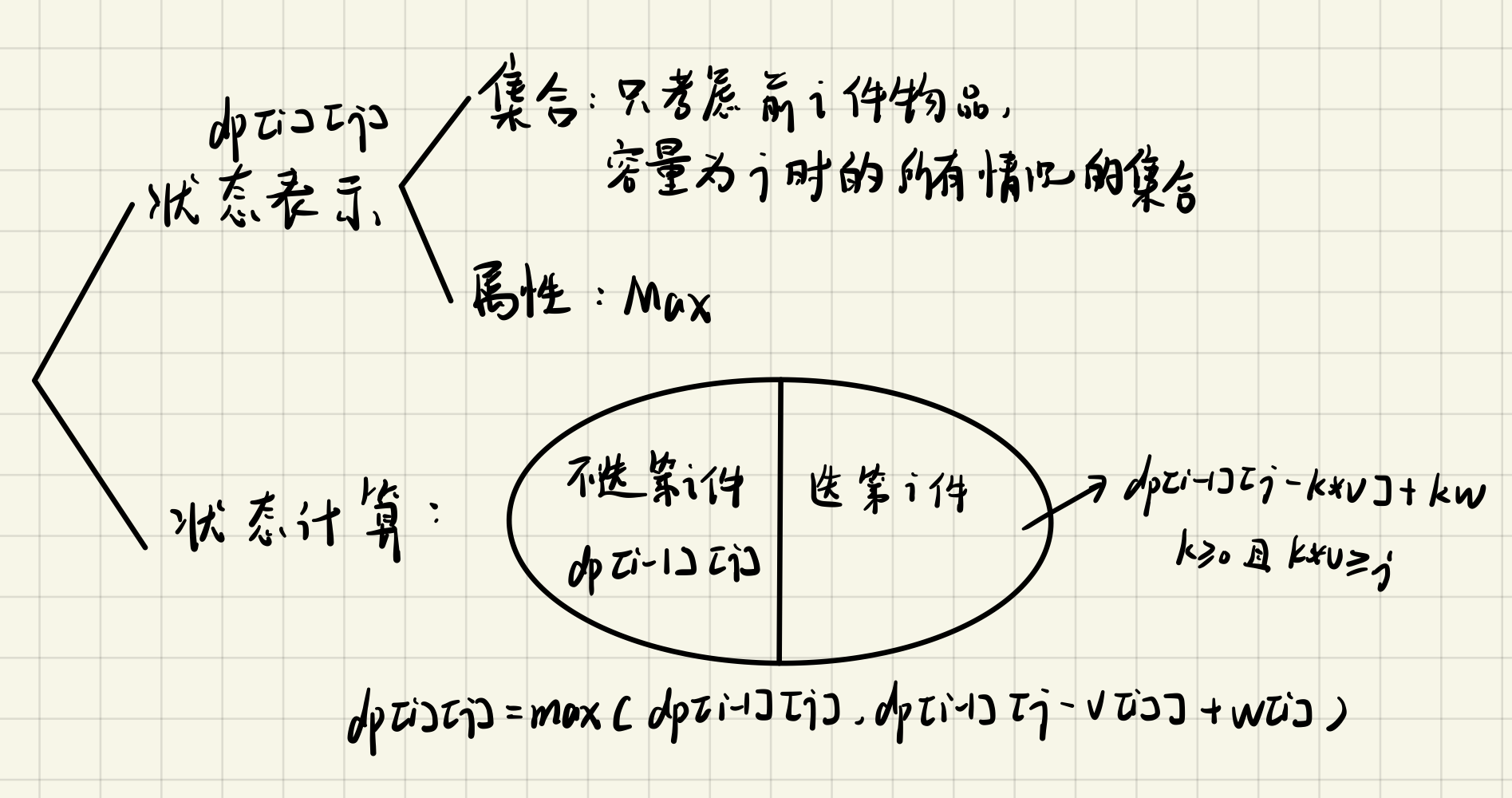
对于每件物品只有取一个或者不取两种操作的背包问题称为01背包，分析法如下：

从上图中可以看出，01背包每次计算i时的状态只用到了i-1的状态，所有可以舍去i这一维，优化成一维dp。

AcWing 423. 采药

1.题面

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。

为此，他想拜附近最有威望的医师为师。

医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入格式
输入文件的第一行有两个整数T和M，用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。

接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式
输出文件包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

数据范围
$1≤T≤1000,$
$1≤M≤100$
输入样例：

70 3
71 100
69 1
1 2

输出样例：

3

2.题目分析

很明显的01背包，直接写就行。

3.代码

#include<bits/stdc++.h>

using namespace std;
const int maxn = 1e4+10;

int dp[maxn],v[maxn],w[maxn];
int main() {
    int t, m;
    cin >> t >> m;
    for(int i = 0; i < m; i++) cin >> v[i] >> w[i];
    for(int i = 0; i < m; i++) {
        for(int j = t; j >= v[i]; j--)
            dp[j] = max(dp[j],dp[j-v[i]] + w[i]);
    }
    cout << dp[t] << endl;
}

AcWing 1024. 装箱问题

1.题面

有一个箱子容量为 V，同时有 n 个物品，每个物品有一个体积（正整数）。

要求 n 个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入格式
第一行是一个整数 V，表示箱子容量。

第二行是一个整数 n，表示物品数。

接下来 n 行，每行一个正整数（不超过10000），分别表示这 n 个物品的各自体积。

输出格式
一个整数，表示箱子剩余空间。

数据范围
$0<V≤20000,$
$0<n≤30$
输入样例：

24
6
8
3
12
7
9
7

输出样例：

0

2.题目分析

要求剩余空间最小，就是要取的体积最大，可以把体积当做价值，转换成01背包问题。

3.代码

#include<bits/stdc++.h>

using namespace std;
const int maxn = 2e4+10;

int dp[maxn],v[maxn],w[maxn];
int main() {
   int V, n;
   cin >> V >> n;
   for(int i = 0; i < n; i++) cin >> v[i];
   for(int i = 0; i < n; i++) {
       for(int j = V; j >= v[i]; j--)
        dp[j] = max(dp[j], dp[j-v[i]] + v[i]);
   }
   cout << V - dp[V] << endl;
}

AcWing 426. 开心的金明

1.题面

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间他自己专用的很宽敞的房间。

更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过N元钱就行”。

今天一早金明就开始做预算，但是他想买的东西太多了，肯定会超过妈妈限定的N元。

于是，他把每件物品规定了一个重要度，分为5等：用整数1~5表示，第5等最重要。

他还从因特网上查到了每件物品的价格（都是整数元）。

他希望在不超过N元（可以等于N元）的前提下，使每件物品的价格与重要度的乘积的总和最大。 

设第j件物品的价格为v[j]，重要度为w[j]，共选中了k件物品，编号依次为j1，j2，…，jk，则所求的总和为： 

$v[j_1]∗w[j_1]+v[j_2]∗w[j_2]+…+v[j_k]∗w[j_k]$

请你帮助金明设计一个满足要求的购物单。

输入格式
输入文件的第1行，为两个正整数N和m，用一个空格隔开。（其中N表示总钱数，m为希望购买物品的个数） 

从第2行到第m+1行，第j行给出了编号为j-1的物品的基本数据，每行有2个非负整数v和p。（其中v表示该物品的价格，p表示该物品的重要度）

输出格式
输出文件只有一个正整数，为不超过总钱数的物品的价格与重要度乘积的总和的最大值（数据保证结果不超过100000000）。

数据范围
$1≤N<30000,$
$1≤m<25,$
$0≤v≤10000,$
$1≤p≤5$
输入样例：

1000 5
800 2
400 5
300 5
400 3
200 2

输出样例：

3900

2.题目分析

很明显的01背包，第k个物品的价值为 $v[j_k]∗w[j_k]$

3.代码

#include <bits/stdc++.h>
using namespace std;
const int N = 30010;
int dp[N];
int main() {
    int n, m;
    cin >> n >>m;
    for(int i = 0; i <m; i++) {
        int v, p;
        cin >> v >> p;
        for(int j = n; j >= v; j--) dp[j] = max(dp[j], dp[j - v] +v*p);
    }
    cout <<dp[n];
}

三、完全背包

物品可以无限选择

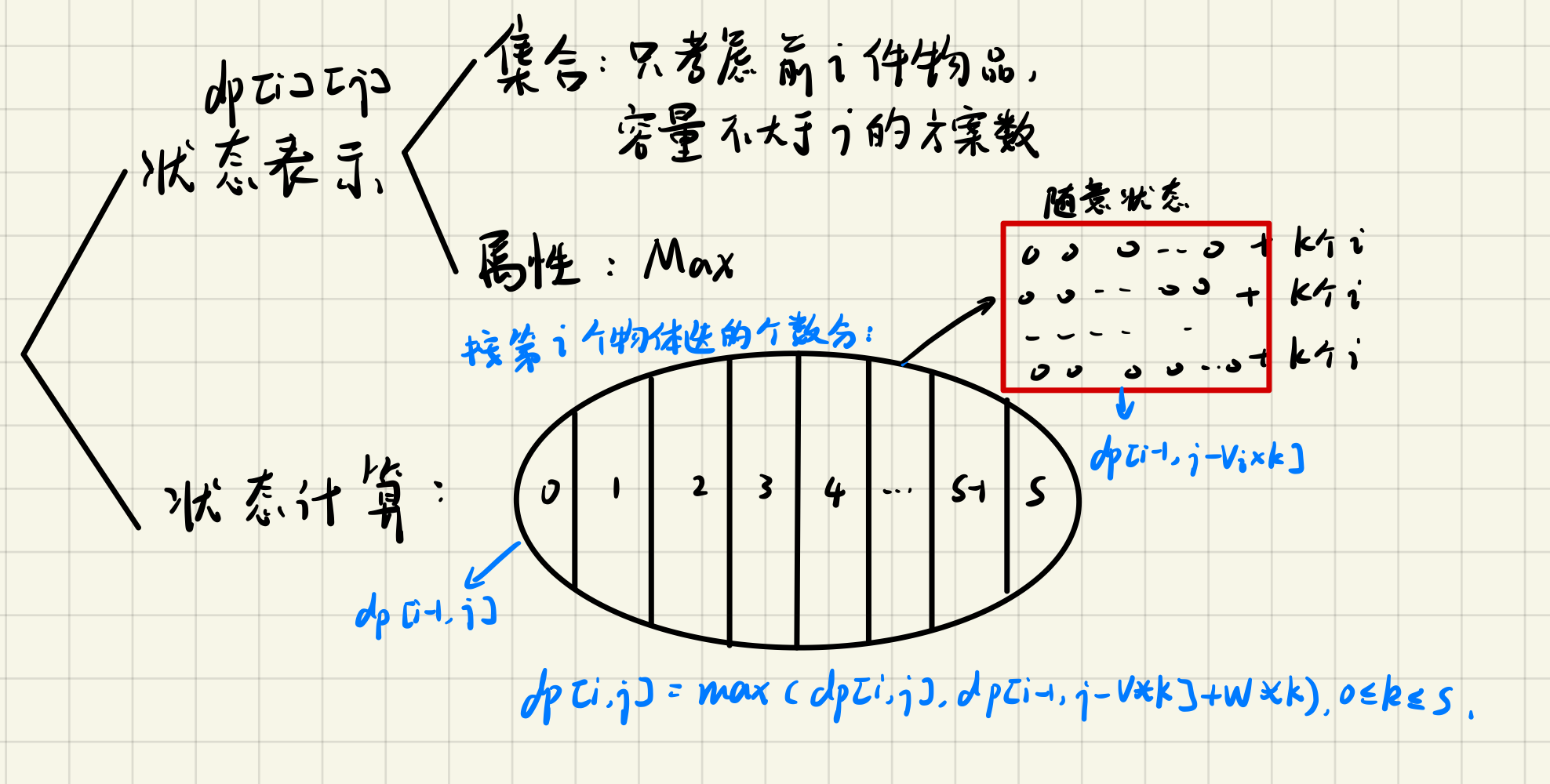
对于第i件物品， 分为选或不选，若选，可以分为选0、1、2、3…个，直到当前体积装不下为止。

AcWing 3. 完全背包问题

1.题面

有 $N$ 种物品和一个容量是 $V$ 的背包，每种物品都有无限件可用。

第 $i$ 种物品的体积是 $v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，$N$，$V$，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行两个整数 $v_i$,$w_i$，用空格隔开，分别表示第 $i$ 种物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
$0<N,V≤1000$
$0<v_i,w_i≤1000$
输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

2.代码

#include<bits/stdc++.h>

using namespace std;
int v[1111], w[1111];
int dp[1111];
int main() {
    int n, V;
    cin >> n >>V;
    for(int i = 0; i <n; i++) cin >> v[i] >>w[i];
    for(int i = 0; i < n; i++) {
        for(int j = v[i]; j <=V; j++) {
            dp[j]= max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    cout << dp[V] <<endl;
}

四、多重背包

多重背包和01背包的不同的是 每个物品可以取多个，但有个上限s，分析如下：

$dp[i][j]$ 的含义和01背包一样，就是状态划分不同，由于第i件物品最多可以取s个，那么就按第i个物品取的个数分：$0,1,2，…，s，$ 其中 $s$ 为第 i 个物品最多选取的数量。任取其中一个状态k，可以将此状态划分为两部分：不包含i的随意组合+k个第i个物品的组合，其中不包含 i 的所有方案状态可以表示为 $dp[i-1][j-v*k]$,故第 $k$ 个状态的方案表示为$dp[i-1][j-v *k] + w[i] * k$,对于 $dp[i][j]$ 只要对所有的方案取max即可。

AcWing 1019. 庆功会

1.题面

为了庆贺班级在校运动会上取得全校第一名成绩，班主任决定开一场庆功会，为此拨款购买奖品犒劳运动员。

期望拨款金额能购买最大价值的奖品，可以补充他们的精力和体力。

输入格式
第一行二个数n，m，其中n代表希望购买的奖品的种数，m表示拨款金额。

接下来n行，每行3个数，v、w、s，分别表示第I种奖品的价格、价值（价格与价值是不同的概念）和能购买的最大数量（买0件到s件均可）。

输出格式
一行：一个数，表示此次购买能获得的最大的价值（注意！不是价格）。

数据范围
$n≤500,m≤6000,$
$v≤100,w≤1000,s≤10$
输入样例：

5 1000
80 20 4
40 50 9
30 50 7
40 30 6
20 20 1

输出样例：

1040

题目分析

多重背包模板题

代码

#include <bits/stdc++.h>

using namespace std;
int dp[6100];
int main() {
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < n; i++) {
        int v, w, s;
        cin >> v >> w >> s;
        for(int j = m; j >=0; j--)
            for(int k = 1; k <= s && k*v<=j; k++)
                dp[j] = max(dp[j], dp[j-k*v] + k*w);
    }
    cout << dp[m] << endl;
}

五、混合背包问题

混合背包问题的物品可能只能选一个，可能可以选一定多个，也可能选无数个，只要对不同类型的物品用不同的状态转移方程即可。

AcWing 7. 混合背包问题

1.题面

有 $N$ 种物品和一个容量是 $V$ 的背包。

物品一共有三类：

第一类物品只能用1次（01背包）；
第二类物品可以用无限次（完全背包）；
第三类物品最多只能用 $s_i$ 次（多重背包）；
每种体积是 $v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，$N$，$V$，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i,w_i,s_i$，用空格隔开，分别表示第 $i$ 种物品的体积、价值和数量。

$s_i=−1$ 表示第 $i$ 种物品只能用1次；
$s_i=0$ 表示第 $i$ 种物品可以用无限次；
$s_i>0$ 表示第 $i$ 种物品可以使用 $s_i$ 次；
输出格式
输出一个整数，表示最大价值。

数据范围
$0<N,V≤1000$
$0<v_i,w_i≤1000$
$−1≤s_i≤1000$
输入样例

4 5
1 2 -1
2 4 1
3 4 0
4 5 2

输出样例：

8

2.题目分析

由于数据范围都是1e3，朴素做法的多重背包会达到1e9级别，故要用二进制优化。其余就是混合背包的一般做法，判断每个物品的类型，然后用不同的状态转移方程去求，就是一个大杂烩。

3.代码

#include <bits/stdc++.h>

using namespace std;

int dp[1111];

int main () {
    int n,v;
    cin >> n >> v;
    for(int i = 0; i < n; i++) {
        int cost, val ,s;
        cin >> cost >> val >> s;
        if(s == 0) {//完全背包
            for(int j = cost; j <= v; j++) dp[j] = max(dp[j], dp[j-cost] + val);
        }
        else {
            if(s==-1) s = 1;//01背包可以看成上限为1的多重背包
            for(int k = 1; k <= s; k*=2){//二进制优化求解多重背包
                for(int j = v; j >= cost*k; j--)
                    dp[j] = max(dp[j],dp[j-cost*k] + val *k);
                s-=k;
            }
            if(s) {
                for(int j = v; j >= cost*s; j--)
                    dp[j] = max(dp[j], dp[j-cost*s] + val * s);
            }
        }
    }
    cout << dp[v] << endl;
}

六、背包问题求方案数

这种题一般可以结合01背包、多重背包、完全背包等一同考察，下面以多重背包为例，分析一下状态表示：

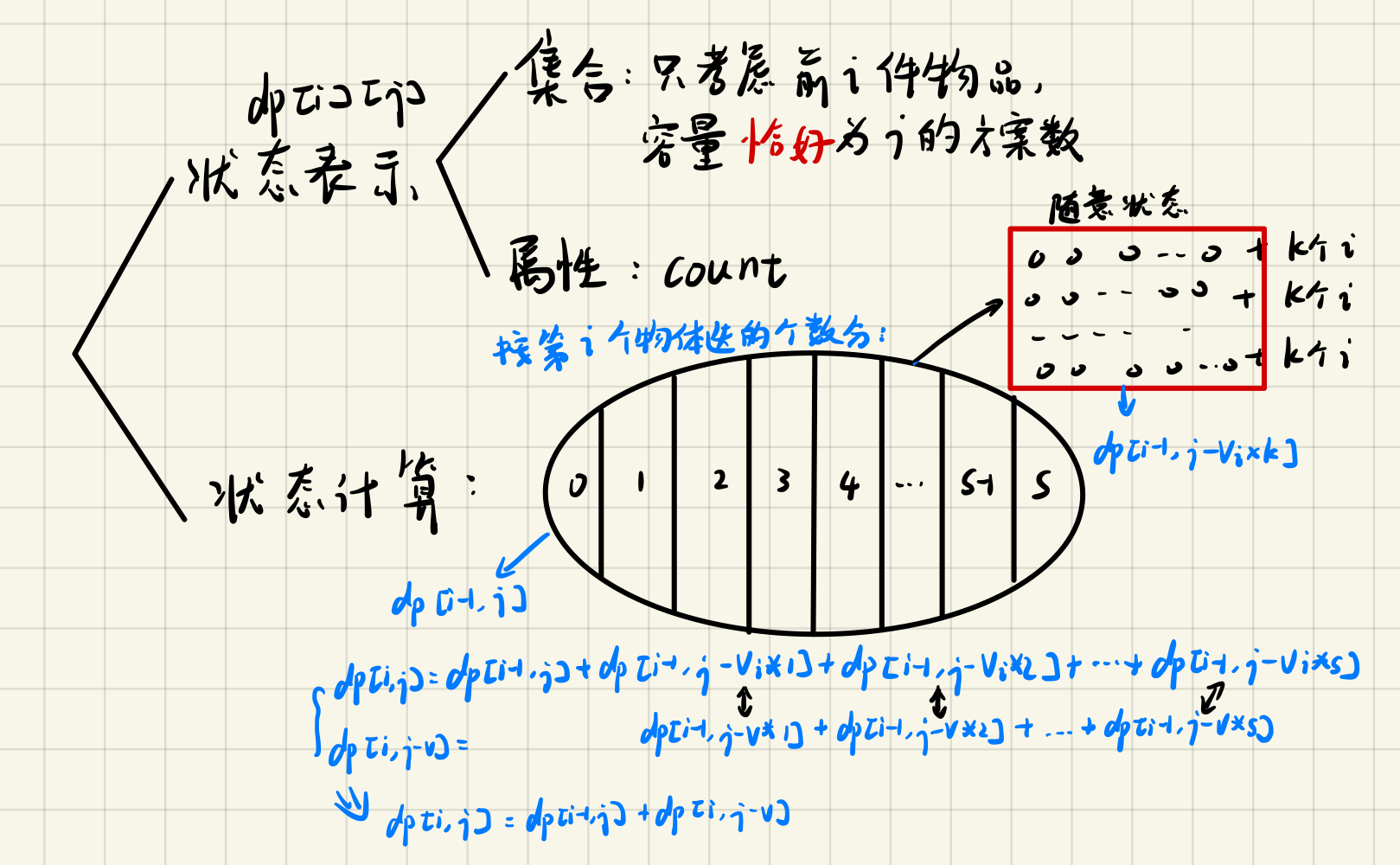
如图所示， $dp[i][j]$ 的定义为只考虑前i件物品，容量恰好为j的方案数，状态按照第i个物品的选择策略来进行划分，分别划分为第i个物品选择 $0,1,2,3,4…s$ 个，其中 $s$ 为第 i 个物品最多选取的数量。任取其中一个状态k，可以将此状态划分为两部分：不包含i的随意组合+k个第i个物品的组合，其中不包含i的随意组合的方案个数正好为 $dp[i-1][j-v*k]$,故第 $k$ 个状态的方案数就是$dp[i-1][j-v *k]$。所以，$dp[i][j]$ 可以表示为图中下方蓝字的式子，通过转换可以变成$dp[i,j] = dp[i-1,j] + dp[i,j-v]$。

AcWing 1023. 买书

1.题面

小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。

问小明有多少种买书方案？（每种书可购买多本）

输入格式
一个整数 $n$，代表总共钱数。

输出格式
一个整数，代表选择方案种数。

数据范围
$0≤n≤1000$
输入样例1：

20

输出样例1：

2

输入样例2：

15

输出样例2：

0

输入样例3：

0

输出样例3：

1

2.题目分析

钱数当背包容量，一共有四种物品，价格当做体积，每本书可以无限买，即求完全背包最优方案的方案数。用上方分析方法即可。

3.代码

#include <bits/stdc++.h>

using namespace std;
int dp[1111];
int v[5] = {10, 20, 50 ,100};
int main() {
    int n;
    cin >> n;
    dp[0] = 1;//体积为0时什么都不买也算一种方案
    for(int i = 0; i < 4; i++)
        for(int j = v[i]; j <= n; j++)
            dp[j] += dp[j- v[i]];
    cout << dp[n] << endl;
}

AcWing 278. 数字组合

1.题面

给定$N$个正整数$A_1,A_2,…,A_N$，从中选出若干个数，使它们的和为$M$，求有多少种选择方案。

输入格式
第一行包含两个整数$N$和$M$。

第二行包含$N$个整数，表示$A_1,A_2,…,A_N$。

输出格式
包含一个整数，表示可选方案数。

数据范围
$1≤N≤100,$
$1≤M≤10000,$
$1≤Ai≤1000$
输入样例：

4 4
1 1 2 2

输出样例：

3

题目分析

和上题基本一样，只不过商品变成了输入的数字，每个数字只能选一个，为01背包，循环体积的时候要从后往前循环（参见01背包二维优化为一维的做法）。

代码

#include<bits/stdc++.h>

using namespace std;
int dp[11111];
int main() {
    int n, m;
    cin >> n >> m;
    dp[0] = 1;
    for(int i =0 ; i < n; i++) {
        int v;
        cin >> v;
        for(int j = m; j >= v; j--) {//从大到小循环体积
            dp[j] += dp[j-v];
        }
    }
    cout << dp[m] << endl;
}

AcWing 1021. 货币系统

1.题面

给你一个 $n$ 种面值的货币系统，求组成面值为 $m$ 的货币有多少种方案。

输入格式
第一行，包含两个整数 $n$ 和 $m$ 。

接下来 $n$ 行，每行包含一个整数，表示一种货币的面值。

输出格式
共一行，包含一个整数，表示方案数。

数据范围
$n≤15,m≤3000$
输入样例：

3 10
1
2
5

输出样例：

10

2.题目分析

也是求方案数，每种面值可以重复选，多重背包求方案数问题。

3.代码

#include <bits/stdc++.h>

using namespace std;
long long dp[3100];
int main() {
    int n,m;
    cin >>n >>m;
    dp[0] = 1;
    for(int i = 0; i <n; i++) {
        int x;
        cin >>x;
        for(int j = x; j <= m; j++) dp[j] += dp[j-x];
    }
    cout << dp[m];
}

AcWing 532. 货币系统

1.题面

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。

为了方便，我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。 

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]× t[i] 的和为 x。

然而，在网友的国度中，货币系统可能是不完善的，即可能存在金额 x 不能被该货币系统表示出。

例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。 

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。 

现在网友们打算简化一下货币系统。

他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m 尽可能的小。

他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入格式
输入文件的第一行包含一个整数 T，表示数据的组数。

接下来按照如下格式分别给出T组数据。 

每组数据的第一行包含一个正整数 n。

接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出格式
输出文件共有T行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。

数据范围
$1≤n≤100,$
$1≤a[i]≤25000,$
$1≤T≤20$
输入样例：

2 
4 
3 19 10 6 
5 
11 29 13 19 17 

输出样例：

2
5

2.题目分析

这题和上一题虽然题目一样但是题目要求完全不同，这题是给你一个n种面值的货币系统，让你尽可能简化这个货币系统，即用尽量少的面值替换原先的货币系统，使得原先货币系统能表示的所有金额简化后也能表示，所有原先不能表示的简化后还是不能表示。

此题还有一个性质，即最优解的元素一定都选自原先的货币系统。

用反证法可以证明：假设最优解由若干个$b_i$构成，且存在$b_k$不属于原货币系统$a_i$,则$b_k$可以用两个以上的原货币系统中的元素表示(如果可以用一个元素表示就和$a_i$相等了,假设：$b_k = a_1+a_2+a_3$)，又因为$b_i$为最优解，每个$a_i$都可以用若干个$b_i$表示，所以$b_k$可以用两个以上的$b_i$表示，那么$b_k$没必要存在，因为与最优解的假设矛盾。

故这题解法就是，看一个货币面值是否可以用其他的面值表示，如果可以表示则扔掉这个，做法就是将面值从小到大排序，然后第i个面值当做背包容量，用前i-1个货币面值去装，如果恰好装满的方案数大于等于1则可以舍去这个面值。

3.代码

#include <bits/stdc++.h>

using namespace std;

const int N = 111;
const int M = 25555;
int a[M],dp[M];

int main(){
    int t;
    cin >> t;
    while(t--) {
        int n;
        cin >> n;
        for (int i = 0; i < n; i++) cin >> a[i];
        sort(a, a+n);
        memset(dp, 0, sizeof dp);
        dp[0] = 1;
        int ans = 0, m = a[n-1];
        for(int i = 0; i < n; i++) {
            if(dp[a[i]] == 0) ans++;
            for(int j = a[i]; j <= m; j++) {
                dp[j] += dp[j-a[i]];
            }
        }
        cout << ans << endl;
    }
}

AcWing 11. 背包问题求方案数

1.题面

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。

第 $i$ 件物品的体积是 $v_i$，价值是$ w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 最优选法的方案数。注意答案可能很大，请输出答案模 $10^9+7$ 的结果。

输入格式
第一行两个整数，$N$，$V$，用空格隔开，分别表示物品数量和背包容积。

接下来有 $N$ 行，每行两个整数 $v_i$,$w_i$，用空格隔开，分别表示第 $i$ 件物品的体积和价值。

输出格式
输出一个整数，表示 方案数 模 $10^9+7$ 的结果。

数据范围
$0<N,V≤1000$
$0<vi,wi≤1000$
输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

2

题目分析

这题要求的是最优选法的方案数，状态定义为体积“恰好”为j，求出所有状态后找最大值，再统计最大值的方案数。

代码

#include <bits/stdc++.h> 

using namespace std;
const int maxn = 1e3+10;
const int mod = 1e9+7;

int dp[maxn], cnt[maxn];

int main() {
    int n, v;
    cin >> n >> v;
    memset(dp, -0x3f, sizeof dp);
    dp[0] = 0;
    cnt[0] = 1;
    for(int i = 0; i < n; i++) {
        int co, val;
        cin >> co >> val;
        for(int j = v; j >= co; j--) {
            int Max = max(dp[j], dp[j-co] + val);
            int sum = 0;
            if(Max == dp[j]) sum += cnt[j];
            if(Max == dp[j-co] + val) sum += cnt[j-co];
            cnt[j] = sum % mod;
            dp[j] = Max;
        }
    }
    int res = 0;
    for(int i = 0; i <= v; i++) res = max(res, dp[i]);//状态表示为恰好，所以要先找到最大值
    int ans = 0;
    for(int i = 0; i <= v; i++) //所有最大值相加
        if(res == dp[i])
        ans += cnt[i];
    cout << ans%mod << endl;
}

七、背包问题求具体方案

以01背包为例，我们知道状态是以是否取第i个物品划分，那么我们只要在求出所有状态的值之后再回溯找一遍每个物品是否被选即可，如果被选，则说明 $dp[i-1][j-v[i]] = dp[i][j] – w[i]$。

AcWing 12. 背包问题求具体方案

题面

有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。

第 $i$ 件物品的体积是 $v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 $1…N$。

输入格式
第一行两个整数，$N$，$V$，用空格隔开，分别表示物品数量和背包容积。

接下来有 $N$ 行，每行两个整数 $v_i$,$w_i$，用空格隔开，分别表示第 $i$ 件物品的体积和价值。

输出格式
输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。

物品编号范围是 $1…N$。

数据范围
$0<N,V≤1000$
$0<vi,wi≤1000$
输入样例
4 5
1 2
2 4
3 4
4 6
输出样例：
1 4

代码

#include <bits/stdc++.h>

using namespace std;
int dp[1111][1111], v[1111], w[1111];
int main() {
    int N, V;
    cin >> N >> V;
    for(int i = 1; i <= N; i++) cin >> v[i] >>w[i];
    //从后往前选物品，方便后面遍历从前往后，保证字典序最小，故下方状态转移方程略微改变
    for(int i = N; i >= 1; i--) {
        for(int j = v[i]; j <= V; j++) {
            dp[i][j] = max(dp[i+1][j], dp[i+1][j-v[i]] +w[i]);
        }
    }
    cout << dp[1][V] << endl;
    int j = V;
    for(int i = 1; i <= N; i++) {
        if(j-v[i] >=0 && dp[i][j] == dp[i+1][j-v[i]] + w[i]) {cout << i << ' ';j-=v[i];}
    }
}

八、分组背包

给你几组物品，要求每组最多只能选一个，求某个最优解。

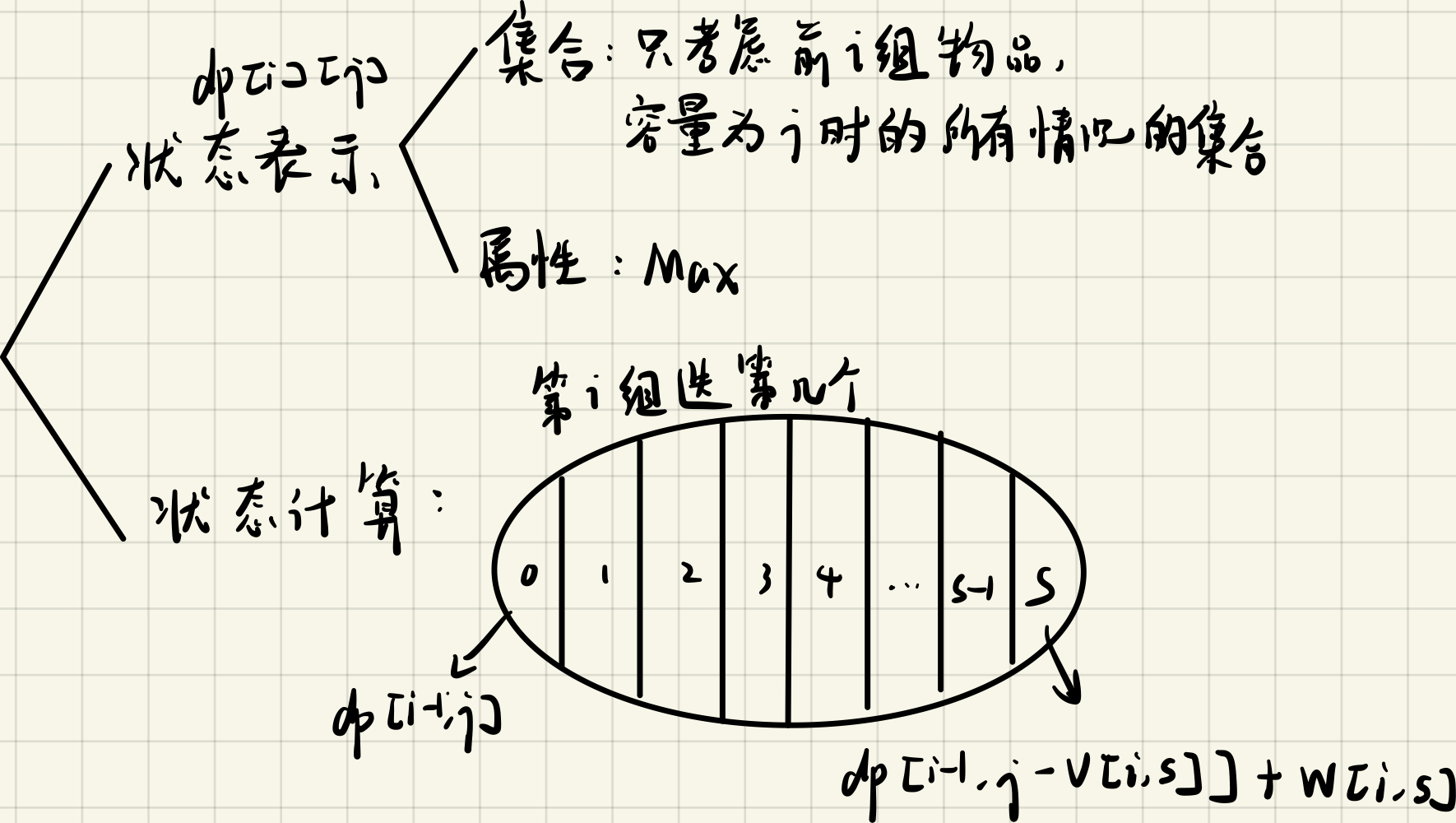
状态转移，其实就是对第 i 组物品分别选一次，维护一下集合的属性（一般为最大值）。

AcWing 1013. 机器分配

1.题面

总公司拥有M台 相同 的高效设备，准备分给下属的N个分公司。

各分公司若获得这些设备，可以为国家提供一定的盈利。盈利与分配的设备数量有关。

问：如何分配这M台设备才能使国家得到的盈利最大？

求出最大盈利值。

分配原则：每个公司有权获得任意数目的设备，但总台数不超过设备数M。

输入格式
第一行有两个数，第一个数是分公司数N，第二个数是设备台数M；

接下来是一个N*M的矩阵，矩阵中的第 i 行第 j 列的整数表示第 i 个公司分配 j 台机器时的盈利。

输出格式
第一行输出最大盈利值；

接下N行，每行有2个数，即分公司编号和该分公司获得设备台数。

答案不唯一，输入任意合法方案即可。

数据范围
$1≤N≤10,$
$1≤M≤15$
输入样例：

3 3
30 40 50
20 30 50
20 25 30

输出样例：

70
1 1
2 1
3 1

2.题目分析

每个公司分配一定数量的机器，每个公司分配的机器数量不同时带来的收益也不同，分配的总机器数不超过M，求最大利润。每个公司分配的数量是确定的，不能既分配一台又分配两台，故将每个公司当做组物品，每组里的物品就是分配的机器数，总分配机器数就是背包容量，分组背包问题。还要求一种合法方案，可以参见背包问题求解具体方案的那一栏，从后往前回溯没件物品，若$dp[i][k] dp[i-1][k-j] + w[i][j]$,则说明找到一种方案，其中k代表当前实际的容量，j用于遍历所有容量。

3.代码

#include <bits/stdc++.h>

using namespace std;

int dp[22][22], w[22][22];
int way[22];
int main() {
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j  <= m; j++)
            cin >> w[i][j];
    }
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j <= m; j++)
            for(int k = 0; k <= j; k++)
                dp[i][j] = max(dp[i][j], dp[i-1][j-k] + w[i][k]);
    }
    cout << dp[n][m] << endl;
    int k = m;
    for(int i = n; i >= 1; i-- ) {
        for(int j = 0; j <= k; j++) {
            if(dp[i][k] == dp[i-1][k-j] + w[i][j]){
                way[i] = j;
                k-=j;
                break;
            }
        }
    }
    for(int i = 1; i <= n; i++) cout << i<< ' ' << way[i] << endl;
}

九、二维费用的背包问题

一般题目有两个限制条件，其实和一维差不多，推导思路和一维很像，同样可以应用到01背包、多重背包、完全背包等。

AcWing 8. 二维费用的背包问题

有 $N$ 件物品和一个容量是 $V$ 的背包，背包能承受的最大重量是 $M$。

每件物品只能用一次。体积是 $v_i$，重量是 $m_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式
第一行两个整数，$N，V,M$，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 $N$ 行，每行三个整数 $v_i,m_i,w_i$，用空格隔开，分别表示第 $i$ 件物品的体积、重量和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
$0<N≤1000$
$0<V,M≤100$
$0<v_i,m_i≤100$
$0<w_i≤1000$
输入样例

4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

输出样例：

8

2.题目分析

看代码就行了，主要区别就是状态表示，类似01背包问题 用三维表示状态，可以优化成二维。

3.代码

#include<bits/stdc++.h>

using namespace std;
const int maxn = 1e3+10;

int dp[maxn][maxn],v[maxn],w[maxn], m[maxn];
int main() {
   int N, M, V;
   cin >> N >> V >> M;
   for(int i = 0; i < N; i++) cin >> v[i] >> m[i] >> w[i];
   for(int i = 0; i < N; i++) {
       for(int j = V; j >= v[i]; j--)
            for(int b = M; b >= m[i]; b--)
                dp[j][b] = max(dp[j][b], dp[j-v[i]][b - m[i]] + w[i]);
   }
    cout << dp[V][M] <<endl;
}

AcWing 1020. 潜水员

1.题面

潜水员为了潜水要使用特殊的装备。

他有一个带2种气体的气缸：一个为氧气，一个为氮气。

让潜水员下潜的深度需要各种数量的氧和氮。

潜水员有一定数量的气缸。

每个气缸都有重量和气体容量。

潜水员为了完成他的工作需要特定数量的氧和氮。

他完成工作所需气缸的总重的最低限度的是多少？

例如：潜水员有5个气缸。每行三个数字为：氧，氮的（升）量和气缸的重量：

3 36 120

10 25 129

5 50 250

1 45 130

4 20 119

如果潜水员需要5升的氧和60升的氮则总重最小为249（1，2或者4，5号气缸）。

你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。

输入格式
第一行有2个整数 m，n。它们表示氧，氮各自需要的量。

第二行为整数 k 表示气缸的个数。

此后的 k 行，每行包括ai，bi，ci，3个整数。这些各自是：第 i 个气缸里的氧和氮的容量及气缸重量。

输出格式
仅一行包含一个整数，为潜水员完成工作所需的气缸的重量总和的最低值。

数据范围
$1≤m≤21,$
$1≤n≤79,$
$1≤k≤1000,$
$1≤a_i≤21,$
$1≤b_i≤79,$
$1≤c_i≤800$
输入样例：

5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119

输出样例：

249

题面分析

将氧气和氦气分别看成一个限制条件，就是一个二维背包问题，求的是满足限制条件的气缸重量的最小值。因此这题我们应该将状态 $dp[i][j][k]$ 设置为对于前 i 个气缸，氧气体积至少为 j ，氦气体积至少为 k 的所有选择的集合。

代码

#include <cstring>
#include <iostream>
using namespace std;
const int N = 22, M = 80;

int n, m, K;
int f[N][M];

int main()
{
    cin >> n >> m >> K;

    memset(f, 0x3f, sizeof f);
    f[0][0] = 0;

    while (K -- )
    {
        int v1, v2, w;
        cin >> v1 >> v2 >> w;
        for (int i = n; i >= 0; i -- )
            for (int j = m; j >= 0; j -- )
                //由于状态含义为“至少是”，故体积至少是负数也存在，只不过用体积为0表示就行
                f[i][j] = min(f[i][j], f[max(0, i - v1)][max(0, j - v2)] + w);
    }
    cout << f[n][m] << endl;
    return 0;
}

AcWing 1022. 宠物小精灵之收服

1.题面

宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。

一天，小智和皮卡丘来到了小精灵狩猎场，里面有很多珍贵的野生宠物小精灵。

小智也想收服其中的一些小精灵。

然而，野生的小精灵并不那么容易被收服。

对于每一个野生小精灵而言，小智可能需要使用很多个精灵球才能收服它，而在收服过程中，野生小精灵也会对皮卡丘造成一定的伤害（从而减少皮卡丘的体力）。

当皮卡丘的体力小于等于0时，小智就必须结束狩猎（因为他需要给皮卡丘疗伤），而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。

当小智的精灵球用完时，狩猎也宣告结束。

我们假设小智遇到野生小精灵时有两个选择：收服它，或者离开它。

如果小智选择了收服，那么一定会扔出能够收服该小精灵的精灵球，而皮卡丘也一定会受到相应的伤害；如果选择离开它，那么小智不会损失精灵球，皮卡丘也不会损失体力。

小智的目标有两个：主要目标是收服尽可能多的野生小精灵；如果可以收服的小精灵数量一样，小智希望皮卡丘受到的伤害越小（剩余体力越大），因为他们还要继续冒险。

现在已知小智的精灵球数量和皮卡丘的初始体力，已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。

请问，小智该如何选择收服哪些小精灵以达到他的目标呢？

输入格式
输入数据的第一行包含三个整数：N，M，K，分别代表小智的精灵球数量、皮卡丘初始的体力值、野生小精灵的数量。

之后的K行，每一行代表一个野生小精灵，包括两个整数：收服该小精灵需要的精灵球的数量，以及收服过程中对皮卡丘造成的伤害。

输出格式
输出为一行，包含两个整数：C，R，分别表示最多收服C个小精灵，以及收服C个小精灵时皮卡丘的剩余体力值最多为R。

数据范围
$0<N≤1000,$
$0<M≤500,$
$0<K≤100$
输入样例1：

10 100 5
7 10
2 40
2 50
1 20
4 20

输出样例1：

3 30

输入样例2：

10 100 5
8 110
12 10
20 10
5 200
1 110

输出样例2：

0 100

2.题目分析

把精灵球的个数当做背包容积1，皮卡丘的血量当做背包容积2，所以用dp[i][j][k]，表示：只考虑前i个小精灵，有j个精灵球，皮卡丘血量为k时的所有取法，类比01背包很好写出状态转移，同样也可以优化成dp[j][k]，至于求皮卡丘最大血量，只要遍历dp[n][i],找到最大的i使得dp[n][i] = = dp[n][m]。

3.代码

#include<bits/stdc++.h>

using namespace std;
const int maxn = 1e3+10;

int dp[maxn][maxn],v[maxn],w[maxn];
int main() {
   int n, m, k;
   cin >> n >> m >> k;
   for(int i = 0; i < k; i++) cin >> v[i] >> w[i];
   for(int i = 0; i < k; i++) {
       for(int j = n; j >= v[i]; j--)
            for(int b = m - 1; b >= w[i]; b--)
                dp[j][b] = max(dp[j][b], dp[j-v[i]][b - w[i]] + 1);
   }
   int ans = dp[n][m - 1];
   for(int i = 0; i <= m; i++) {
       if(ans==dp[n][i]){
            cout << ans <<' ' << m - i << endl;
            break;
       }
   }
}

十、有依赖的背包问题

物品之间一般有种依赖关系，比如若要选择物品a，前提是必须先选物品b，诸如此类的问题称为有依赖的背包问题。以树形依赖关系的背包问题为例：

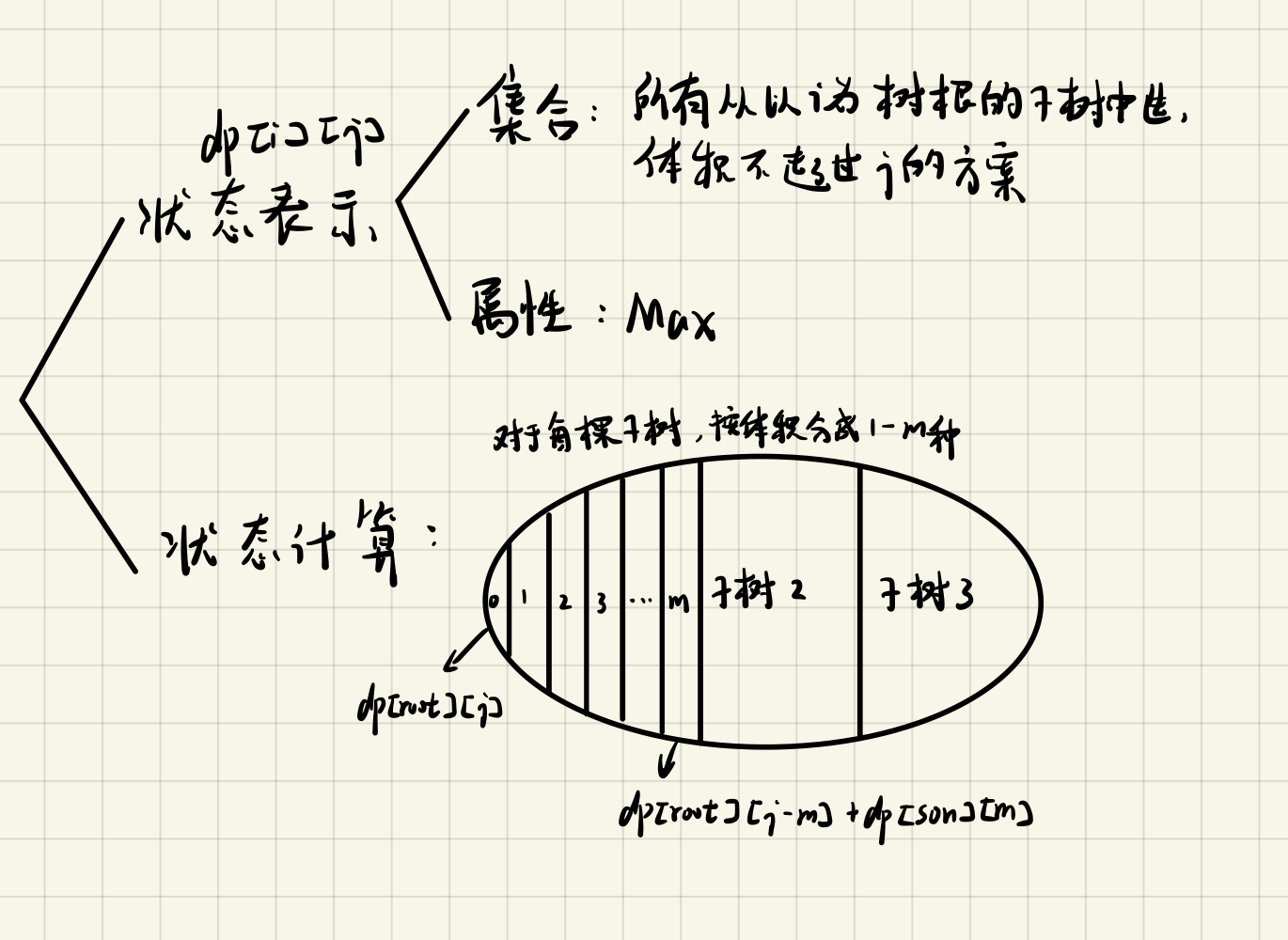
由于树节点可能很多，若有n个节点，按照方案划分的话可能有$2^n$级别的时间复杂度，故用体积来划分状态，由于每种状态之间互斥，可以用分组背包的思想来求解，对于树形的依赖关系，参考树形dp，dfs进行求解。

AcWing 10. 有依赖的背包问题

1. 题面

有 $N$ 个物品和一个容量是 $V$ 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

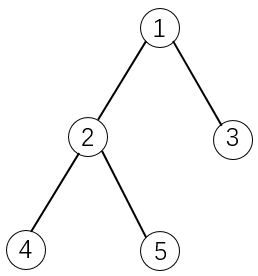
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 $i$，体积是 $v_i$，价值是 $w_i$，依赖的父节点编号是 $p_i$。物品的下标范围是 $1…N$。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数 $N$，$V$，用空格隔开，分别表示物品个数和背包容量。

接下来有 $N$ 行数据，每行数据表示一个物品。
第 $i$ 行有三个整数 $v_i,w_i,p_i$，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 $pi=−1$，表示根节点。 数据保证所有物品构成一棵树。

输出格式
输出一个整数，表示最大价值。

数据范围
$1≤N,V≤100$
$1≤v_i,w_i≤100$

父节点编号范围：

• 内部结点：$1≤pi≤N;$
• 根节点 $pi=−1;$

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11

题目分析

看前面分析实现即可。

代码

#include <bits/stdc++.h>

using namespace std;

int h[1111], to[1111], dp[1111][1111], v[1111], w[1111], idx,ne[1111];
int N, V, root;
void add(int a, int b){
    to[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
} 

void dfs(int root) {
    for(int i = h[root]; i != -1; i = ne[i]) {//循环物品
        int son = to[i];
        dfs(son);
        for(int j = V - v[root]; j >= 0; j--)//循环体积，预先减去v[root]，给根节点留空
            for(int k = 0; k <= j; k++)//循环决策
                dp[root][j] = max(dp[root][j], dp[root][j-k]+ dp[son][k]);
    }
    //对于体积大于根节点的所有点来说，要再加上根节点的权值
    for(int i = V; i >= v[root]; i--) dp[root][i] = dp[root][i-v[root]] + w[root];
    //所有小于根节点体积的点直接为0
    for(int i = 0; i < v[root]; i++) dp[root][i] = 0;
}

int main(){
    memset(h, -1, sizeof h);

    cin >> N >> V;
    for(int i = 1; i <= N; i++) {
        int p;
        cin >> v[i] >> w[i] >> p;
        if(p == -1) root = i;
        else add(p, i);
    }

    dfs(root);
    cout << dp[root][V];
}

十一、结语

刷了那么多背包的题，总算有点体会了，背包的代码基本上都很短，还是很靠思维的，难点在于状态表示和状态转移。同时，背包问题十分灵活，根据不同问题，状态表示也不同，比如可能将体积设为“不大于”、“恰好是”、“不少于”三种的状态表示虽然相同，但是在代码实现上还是有一定不同的，需要根据实际情况考虑。另外，有些题目可能表面看不出是背包问题， 但是通过贪心等手段可以转换成背包，这种题目难度也大。