一、什么是状态机？

定义

有限状态机，（英语：Finite-state machine, FSM），又称有限状态自动机，简称状态机，是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。

先来解释什么是“状态”（ State ）。现实事物是有不同状态的，例如水，就有固液气三种状态。我们通常所说的状态机是有限状态机，也就是说被描述的事物的状态是有限的，水的状态就是三个——固液气。

状态机，也就是 State Machine ，不是指一台实际机器，而是指一个数学模型。说白了，一般就是指一张状态转换图。例如，根据水三种状态的转变规律，我们可以抽象出下面这么一个图。

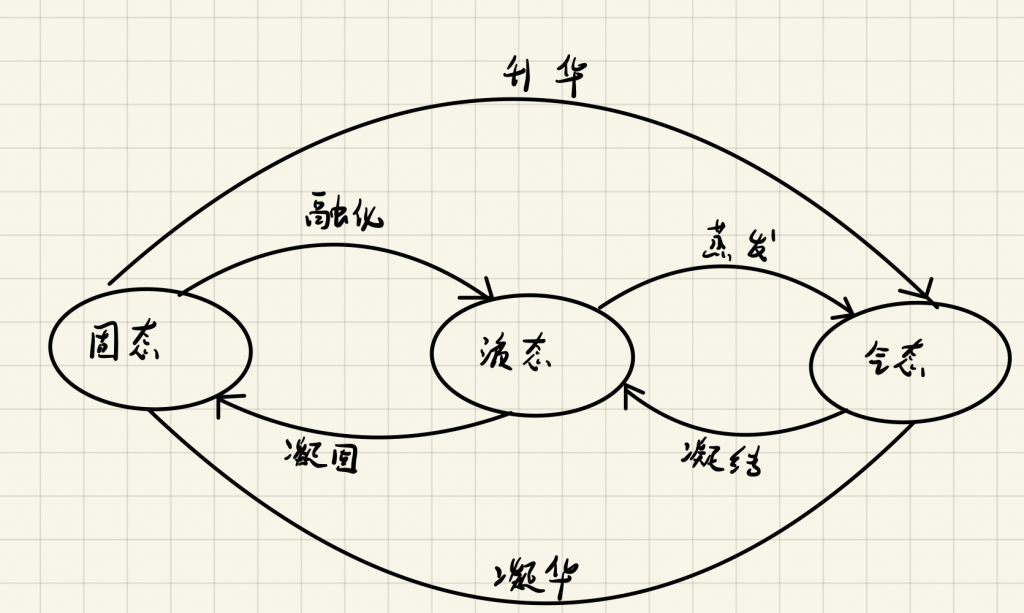
水有三个状态，固态下，如果升华，那么状态就会切换为气态，如果融化，状态就切换为液态。

状态机的全称是有限状态自动机，自动两个字也是包含重要含义的。给定一个状态机，同时给定它的当前状态以及输入，那么输出状态时可以明确的运算出来的。例如对于水，给定初始状态为固态，给定输入“融化”，那么下一个状态时可以运算出来的（液态）。

四大概念

下面来给出状态机的四大概念。

第一个是 State ，状态。一个状态机至少要包含两个状态。例如上面水的例子，有固液气三种状态。

第二个是 Event ，事件。事件就是执行某个操作的触发条件或者口令。对于水，“加热”就是一个事件。

第三个是 Action ，动作。事件发生以后要执行动作。例如事件是“加热”，动作是“冰逐渐融化”。编程的时候，一个 Action 一般就对应一个函数。

第四个是 Transition ，变换。也就是从一个状态变化为另一个状态。例如“升华过程”就是一个变换。

上述参考：什么是状态机？ Peter 王广忠

算法竞赛中的应用

初学状态机，感觉和背包问题很像，其实有很大的区别。以01背包为例，对于一个物品01背包只有选或不选两种操作，这只能算一种结果，不存在所谓的“状态”。而状态机描述的是一个过程，每个过程抽象为一个点，每个点之间可能有一条有向边相连，表示可以从A状态转变到B状态。由于是个过程，必然存在时间的推移（或者某种步骤的向前移动），每时刻状态都会变化，也会伴随此时刻此状态所记录的的值的变化，运用DP记录每个状态的不同时刻的某个值发生的变化，维护最优解。（可能比较抽象，来几题就能体会了）

二、例题

所有题目来自 Acwing 算法提高课

AcWing 1049. 大盗阿福

1.题面

阿福是一名经验丰富的大盗。趁着月黑风高，阿福打算今晚洗劫一条街上的店铺。

这条街上一共有 N 家店铺，每家店中都有一些现金。

阿福事先调查得知，只有当他同时洗劫了两家相邻的店铺时，街上的报警系统才会启动，然后警察就会蜂拥而至。

作为一向谨慎作案的大盗，阿福不愿意冒着被警察追捕的风险行窃。

他想知道，在不惊动警察的情况下，他今晚最多可以得到多少现金？

输入格式
输入的第一行是一个整数 $T$，表示一共有 $T$ 组数据。

接下来的每组数据，第一行是一个整数 $N$ ，表示一共有 $N$ 家店铺。

第二行是 $N$ 个被空格分开的正整数，表示每一家店铺中的现金数量。

每家店铺中的现金数量均不超过1000。

输出格式
对于每组数据，输出一行。

该行包含一个整数，表示阿福在不惊动警察的情况下可以得到的现金数量。

数据范围
$1≤T≤50,$
$1≤N≤105$
输入样例：

2
3
1 8 2
4
10 7 6 14

输出样例：

8
24

样例解释
对于第一组样例，阿福选择第2家店铺行窃，获得的现金数量为8。

对于第二组样例，阿福选择第1和4家店铺行窃，获得的现金数量为10+14=24。

2.题目分析

画出状态机如下图：

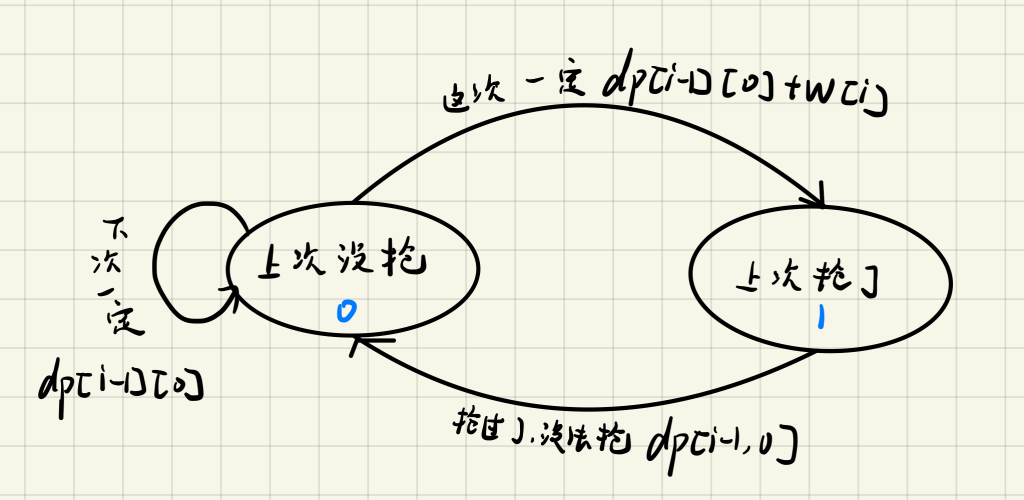
$dp[i][j]$ 表示当前在第i个店铺，j表示对应的状态，只有01两种。
对于第i个店铺，有两种状态，上次抢过或者上次没抢，分别用1和0表示。若处于“上次没抢”状态，强盗可以选择“抢”，变成“上次抢了”的状态（注意，状态转移后，就进入下一时刻，即第i+1个店铺，此时由于抢了第i个店铺，所有处于“上次抢了”的状态），也可以还是“不抢”，保持“上次没抢状态”。若处于“上次抢了”的状态，由于要隔这抢，所以强盗只能执行“不抢”，转移到“上次没抢”状态。强盗从第一个店铺走到最后一个店铺，每走一个店铺，当前所有合法的状态就会通过其中一条边变成相应的一种状态。记录所有的状态中的max，就能求出最优解。

3.代码

#include <bits/stdc++.h>

using namespace std;
const int maxn = 1e5+10;
int a[maxn];
int dp[maxn][2];
int main(){
    int t;
    cin >> t;
    while(t--){
        int n;
        cin >> n;
        for(int i = 0; i < n; i++) scanf("%d",&a[i]);
        dp[1][0] = 0, dp[0][0] = 0;
        for(int i = 0; i < n; i++) {
            dp[i][0] = max(dp[i-1][0],dp[i-1][1]);
            dp[i][1] = dp[i-1][0] + a[i];
        }
        cout << max(dp[n-1][0],dp[n-1][1]) << endl;
    }
}

AcWing 1057. 股票买卖 IV

1.题面

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法来计算你所能获取的最大利润，你最多可以完成 $k$ 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。一次买入卖出合为一笔交易。

输入格式
第一行包含整数 $N$ 和 $k$，表示数组的长度以及你可以完成的最大交易数量。

第二行包含 $N$ 个不超过 10000 的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
$1≤N≤105,$
$1≤k≤100$
输入样例1：

3 2
2 4 1

输出样例1：

2

输入样例2：

6 2
3 2 6 5 0 3

输出样例2：

7

样例解释
样例1：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

样例2：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7.

2.题目分析

状态图如下，其中 $dp[i][j][k]$ 表示第i天，已经操作j次，处于状态k时钱包余额。

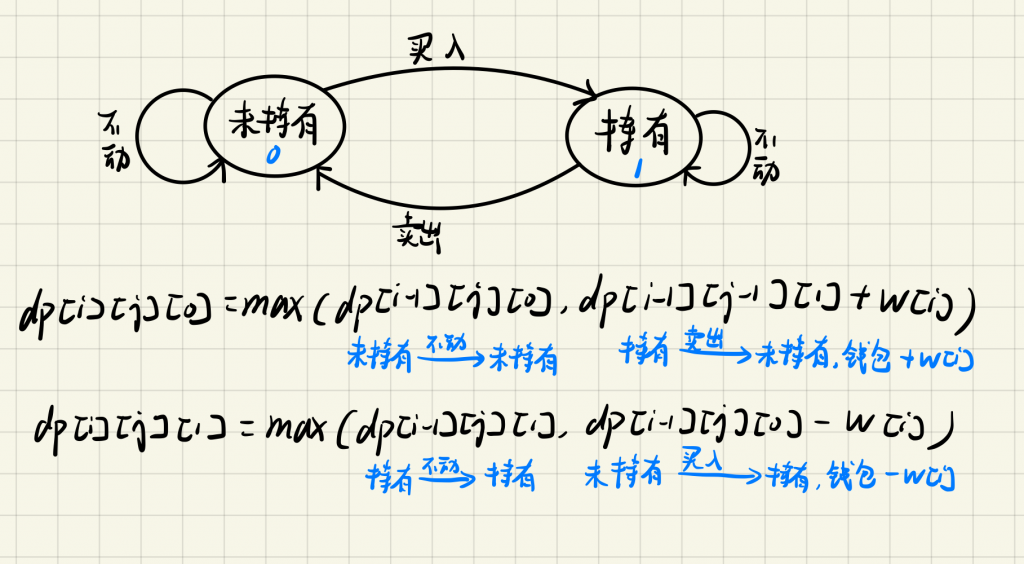
对于初始化这样考虑：一开始处于第0天，操作0次，处于未持有状态0钱包余额为0，这种状态合法，即$dp[0][0][0] = 0$，其余皆不合法，初始化为无穷值，这里由于求最大值，故初始化为负无穷。

3.代码

#include <bits/stdc++.h>

using namespace std;
const int maxn = 1e5+10;

int dp[maxn][111][2], w[maxn];

int main() {
    int n, k;
    cin >> n >> k;
    for(int i = 1; i <=n; i++) scanf("%d",&w[i]);
    memset(dp,-0x3f,sizeof dp);
    dp[0][0][0] = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j <= k; j++) {
            dp[i][j][0] = dp[i-1][j][0];
            if(j >= 1) dp[i][j][0] = max(dp[i][j][0],dp[i-1][j-1][1] + w[i]);
            dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j][0] - w[i]);
        }
    }
    int ans = 0;
    for(int i = 0; i <= k; i++) ans = max(ans, dp[n][i][0]);
    cout << ans << endl;
}

AcWing 1058. 股票买卖 V

1.题面

给定一个长度为 $N$ 的数组，数组中的第 $i$ 个数字表示一个给定股票在第 $i$ 天的价格。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
输入格式
第一行包含整数 $N$，表示数组长度。

第二行包含 $N$ 个不超过 10000 的正整数，表示完整的数组。

输出格式
输出一个整数，表示最大利润。

数据范围
$1≤N≤105$
输入样例：

5
1 2 3 0 2

输出样例：

3

样例解释
对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]，第一笔交易可得利润 2-1 = 1，第二笔交易可得利润 2-0 = 2，共得利润 1+2 = 3。

2.题面分析

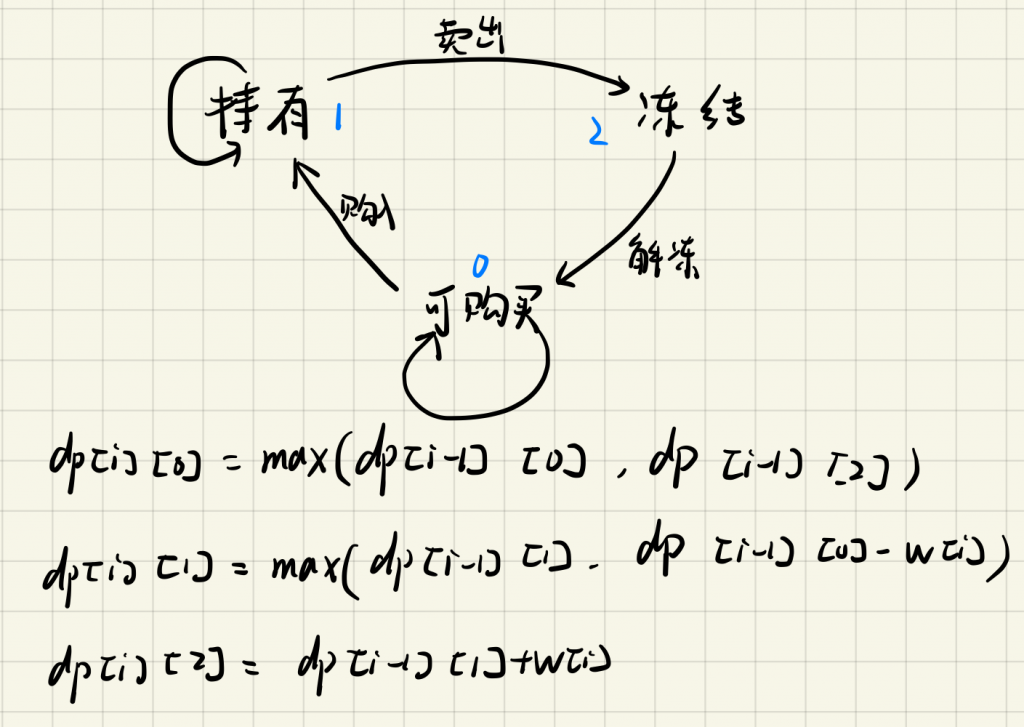
$dp[i][j]$ 表示第i天处于状态j时的余额。

3.代码

#include <bits/stdc++.h>

using namespace std;
const int maxn = 1e5+10;

int dp[maxn][2], w[maxn];

int main() {
    int n, k;
    cin >> n;
    for(int i = 1; i <=n; i++) scanf("%d",&w[i]);
    memset(dp,-0x3f,sizeof dp);
    dp[0][0] = 0;
    for(int i = 1; i <= n; i++) {
        dp[i][0] = max(dp[i-1][0], dp[i-1][2]);
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - w[i]);
        dp[i][2] = dp[i-1][1] + w[i];
    }
    cout << max(dp[n][0],dp[n][2]) << endl;
}

AcWing 1052. 设计密码

1.题面

你现在需要设计一个密码 $S$，$S$ 需要满足：

• $S$ 的长度是 $N$；
• $S$ 只包含小写英文字母；
• $S$ 不包含子串 $T$；
  例如：$abc$ 和 $abcde$ 是 $abcde$ 的子串，$abd$ 不是 $abcde$ 的子串。

请问共有多少种不同的密码满足要求？

由于答案会非常大，请输出答案模 $10^9+7$ 的余数。

输入格式
第一行输入整数$N$，表示密码的长度。

第二行输入字符串$T$，$T$中只包含小写字母。

输出格式
输出一个正整数，表示总方案数模 $10^9+7$ 后的结果。

数据范围
$1≤N≤50,$
$1≤|T|≤N，|T|是T的长度。$

输入样例1：

2
a

输出样例1：

625

输入样例2：

4
cbc

输出样例2：

456924

2.题目分析

可以看这篇，写的很不错了

3.代码

#include <bits/stdc++.h>

using namespace std;
const int mod = 1e9+7;
char p[100];
int ne[111];
int dp[111][111];//S串的第i个，p串的第j个位置对应的个数。

int main(){
    int n;
    cin >> n;
    cin >> p+1;
    int m = strlen(p+1);
    for(int i = 2, j = 0; i <= m; i++) {
        while(j && p[i] != p[j+1]) j = ne[j];
        if(p[i] == p[j+1]) j++;
        ne[i] = j;
    }
    dp[0][0] = 1;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j <= m; j ++) {
            for(char k = 'a'; k <= 'z' ;k++){
                int u = j;
                while(u && k != p[u+1]) u = ne[u];
                if(k == p[u+1]) u ++;
                if(u < m) dp[i+1][u] = (dp[i+1][u] + dp[i][j])%mod;
            }
        }
    }
    int res = 0;
    for(int i = 0; i <= m; i++) res = (res + dp[n][i]) % mod;
    cout << res;
}