AcWing 282. 石子合并(模板题)
1.题面
设有N堆石子排成一排,其编号为1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这N堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有4堆石子分别为 1 3 5 2, 我们可以先合并1、2堆,代价为4,得到4 5 2, 又合并 1,2堆,代价为9,得到9 2 ,再合并得到11,总代价为4+9+11=24;
如果第二步是先合并2,3堆,则代价为7,得到4 7,最后一次合并代价为11,总代价为4+7+11=22。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数N表示石子的堆数N。
第二行N个数,表示每堆石子的质量(均不超过1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
$1≤N≤300$
输入样例:
4
1 3 5 2
输出样例:
22
分析
核心:最后一次合并一定是左边连续的一部分和右边连续的一部分进行合并
状态表示:$f[i][j]$ 表示将 $i$ 到 $j$ 合并成一堆的方案的集合,属性 Min
状态计算:
(1) $i<j$ 时,$f[i][j]=min(f[i][k]+f[k+1][j]+s[j]−s[i−1]$),k从i到j-1,表示i到k这一堆和k+1到j这一堆合并,s是前缀和用于求合并这两堆所需要的代价。
(2) $i=j$ 时, $f[i][i]=0$ (合并一堆石子代价为 0)
$f[1][n]$ 即为答案。
初始化:求最小值dp初始化为无穷大,否则为无穷小。
模板:
for (int len = 2; len <= n; len++) //区间长度
for (int i = 1; i + len - 1 <= n; i++) { //枚举起点
dp[i][j] = -0x3f3f3f3f; //初始化
int j = i + len - 1; //区间终点
for (int k = i; k < j; k++) { //枚举分割点,构造状态转移方程
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + w[i][j]);
}
}
代码:
#include <bits/stdc++.h>
using namespace std;
int dp[310][310];
int qian[310];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
qian[i] = qian[i - 1] + x;
}
for (int len = 2; len <= n; len++) {
for (int i = 1; i <= n - len + 1; i++) {
int j = i + len - 1;
dp[i][j] = 0x3f3f3f3f;
for (int k = i; k <= j - 1; k++) {
dp[i][j] = min(dp[i][j],dp[i][k] + dp[k + 1][j] + qian[j] - qian[i - 1]);
}
}
}
cout << dp[1][n] << endl;
}
AcWing 1068. 环形石子合并(环形区间变形)
1.题面
将 $n$ 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 $n$ 及每堆的石子数,并进行如下计算:
选择一种合并石子的方案,使得做 $n−1$ 次合并得分总和最大。
选择一种合并石子的方案,使得做 $n−1$ 次合并得分总和最小。
输入格式
第一行包含整数 $n$,表示共有 $n$ 堆石子。
第二行包含 $n$ 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
$1≤n≤200$
输入样例:
4
4 5 9 4
输出样例:
43
54
2.分析
环形的一个区间,朴素做法可以这样考虑:
对于两堆石子合并相当于将其连边,那么n堆一共连n-1条边,所以这个环形最后会留下一个缺口,只要枚举一遍最后缺口的位置,剩下就转换成了一条直线形式的石子合并了(上题),已知直线的石子合并复杂度达到了$o(n^3)$,那么这种朴素做法达到了$o(n^4)$,十分恐怖,不可取。
优化方法是这样的:
将环形展开成一条直序列,并在序列后复制一段一样的序列,如(12345组成的环,展开后变成1234512345),然后在这个2n长度的直线上进行最大长度为n的区间dp,复杂度为$o(2 * n^3)$。这也是环形数据处理的一般思路,可以记住。
3.代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 410;
int dp[maxn][maxn], dp2[maxn][maxn], s[maxn], w[maxn];
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> w[i], w[i + n] = w[i];
for (int i = 1; i <= 2 * n; i++) s[i] = s[i - 1] + w[i];
for (int len = 2; len <= n; len++) {
for (int l = 1; l + len - 1 <= 2 * n; l++) {
int r = l + len - 1;
dp[l][r] = 0x3f3f3f3f;
dp2[l][r] = -0x3f3f3f3f;
for (int k = l; k <= r - 1; k++) {
dp[l][r] =
min(dp[l][r], dp[l][k] + dp[k + 1][r] + s[r] - s[l - 1]);
dp2[l][r] =
max(dp2[l][r], dp2[l][k] + dp2[k + 1][r] + s[r] - s[l - 1]);
}
}
}
int ans1 = 0x3f3f3f3f, ans2 = -0x3f3f3f3f;
for (int i = 1; i <= n; i++) {
ans1 = min(ans1, dp[i][i + n - 1]);
ans2 = max(ans2, dp2[i][i + n - 1]);
}
cout << ans1 << endl << ans2 << endl;
}
AcWing 320. 能量项链(环形区间变形)
1.题面
在Mars星球上,每个Mars人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是Mars人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 mrn(Mars单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设N=4,4颗珠子的头标记与尾标记依次为(2,3) (3,5) (5,10) (10,2)。
我们用记号⊕表示两颗珠子的聚合操作,(j⊕k)表示第 j,k 两颗珠子聚合后所释放的能量。则
第4、1两颗珠子聚合后释放的能量为:(4⊕1)=1023=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为((4⊕1)⊕2)⊕3)= 1023+1035+10510=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是N个用空格隔开的正整数,所有的数均不超过1000,第 i 个数为第 i 颗珠子的头标记,当i<N时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第1颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
$4≤N≤100,$
$1≤E≤2.1∗10^9$
输入样例:
4
2 3 5 10
输出样例:
710
2.分析
由题目样例可以看出 2 3 5 10 是一个 (2,3) (3,5) (5,10) (10,2) 的环形结构,我们把多余的数字剔除,剩下的就是2 3 5 10 2(两个相邻的珠子的收尾值相同,可以只用一个数字代替),那么其中一种合并操作就是 2 3 5 合并变成 2 5 ,获得 2 * 3 * 5 的能量,故 2 3 5 10这样的一个环形结构,可以以任意一个数字为缺口展开,比如以5为缺口展开就变成了 5 10 2 3 5 ,以3展开变成 3 5 10 2 3 。类似上题思路, 2 3 5 10 可以展开成 2 3 5 10 2 3 5 10 ,然后枚举长度为 n+1 的区间,就相当于枚举了以每个数字为缺口的情况。
3.代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 210;
int dp[maxn][maxn], w[maxn];
int main(){
int n;
cin >> n;
for(int i = 1; i <= 2*n; i++) cin >> w[i], w[i+n] = w[i];
for(int len = 2; len <= n+1; len ++) {
for(int l = 1; l + len <= 2*n; l++){
int r = l + len;
dp[l][r] = -0x3f3f3f3f;
for(int k = l+1; k <= r-1; k++) {
dp[l][r] = max(dp[l][r], dp[l][k] + dp[k][r] + w[l] * w[r] * w[k]);
cout <<l << " + " << r << ' ' << dp[l][r] << endl;
}
}
}
int ans = -1;
for(int i = 1; i <= n; i++){
ans = max(ans, dp[i][i+n]);
}
cout << ans << endl;
}
AcWing 1069. 凸多边形的划分(环形+高精度)
1.题面
给定一个具有 $N$ 个顶点的凸多边形,将顶点从 $1$ 至 $N$ 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 $N−2$ 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 $N$,表示顶点数量。
第二行包含 $N$ 个整数,依次为顶点 $1$ 至顶点 $N$ 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
$N≤50,$
数据保证所有顶点的权值都小于$10^9$
输入样例:
5
121 122 123 245 231
输出样例:
12214884
2.题目分析
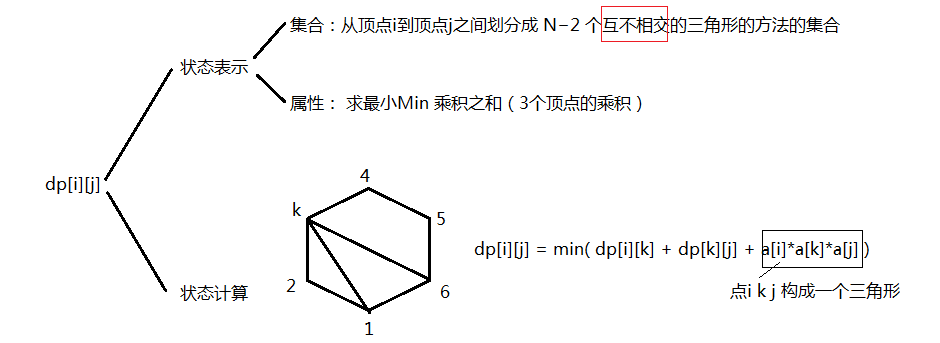
可以发现此题和上一题的状态转移完全相同,但含义不同,并且此题数据范围很大,得用高精度实现。
3.
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int M = 35, N = 55;
void add(LL *a, LL *b) {
static LL c[M];//static 避免函数重复调用时重复开数组浪费时间
memset(c, 0, sizeof c);
for(int i = 0, t = 0; i < M; i++) {
t+=a[i]+b[i];
c[i] = t%10;
t /= 10;
}
memcpy(a, c, sizeof(c));
}
void mul(LL *a, LL b) {
static LL c[M];
memset(c, 0, sizeof c);
LL t = 0;//由于第一位是W[i],所以t可能会超int,得设为LL
for(int i = 0; i < M; i++) {
t+=a[i]*b;
c[i] = t%10;
t /= 10;
}
memcpy(a, c, sizeof(c));
}
int cmp(LL *a, LL *b) {
for(int i = M-1; i >= 0 ; i--)//M-1是最高位
{
if(a[i] > b[i]) return 1;
else if(a[i] < b[i]) return -1;
}
return 0;
}
void print(LL *a)
{
int k = M - 1;
while (k && !a[k]) k -- ;//先过滤前导0
while (k >= 0) cout << a[k -- ];
cout << endl;
}
LL dp[N][N][M];
int w[N];
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; i++) cin >> w[i];
LL temp[M];
for(int len = 3; len <= n; len++)
for(int i = 1; i + len -1 <= n; i++){
int j = i + len - 1;
dp[i][j][M-1] = 1;
for(int k = i+1; k <= j-1; k++){
memset(temp, 0, sizeof temp);
temp[0] = w[i];//直接将temp的第一位赋为w[i],比较方便
mul(temp, w[j]);
mul(temp, w[k]);
add(temp, dp[i][k]);
add(temp, dp[k][j]);
if(cmp(temp,dp[i][j]) == -1) memcpy(dp[i][j], temp, sizeof temp);
}
}
print(dp[1][n]);
}
AcWing 479. 加分二叉树
1.题面
设一个n个节点的二叉树tree的中序遍历为(1,2,3,…,n),其中数字1,2,3,…,n为节点编号。
每个节点都有一个分数(均为正整数),记第i个节点的分数为$d_i$,tree及它的每个子树都有一个加分,任一棵子树subtree(也包含tree本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为1。叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第1行:一个整数n,为节点个数。
第2行:n个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第1行:一个整数,为最高加分(结果不会超过int范围)。
第2行:n个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
$n<30$
输入样例:
5
5 7 1 2 10
输出样例:
145
3 1 2 4 5
2.分析
状态表示:f[i][j] 表示中序遍历是 w[i ~ j] 的所有二叉树的得分的最大值。
状态计算:f[i][j] = max(f[i][k - 1] * f[k + 1][j] + w[k]),即将f[i][j]表示的二叉树集合按根节点分类,则根节点在 k 时的最大得分即为 f[i][k - 1] * f[k + 1][j] + w[k],则f[i][j]即为遍历 k 所取到的最大值。
在计算每个状态的过程中,记录每个区间的最大值所对应的根节点编号。
那么最后就可以通过DFS求出最大加分二叉树的前序遍历了。
3.代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 30;
int n;
int w[N];
int f[N][N], g[N][N];
void dfs(int l, int r)
{
if (l > r) return;
int k = g[l][r];
cout << k << ' ';
dfs(l, k - 1);
dfs(k + 1, r);
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
for (int len = 1; len <= n; len ++ )
for (int l = 1; l + len - 1 <= n; l ++ )
{
int r = l + len - 1;
if (len == 1) f[l][r] = w[l], g[l][r] = l;
else
{
for (int k = l; k <= r; k ++ )
{
int left = k == l ? 1 : f[l][k - 1];
int right = k == r ? 1 : f[k + 1][r];
int score = left * right + w[k];
if (f[l][r] < score)
{
f[l][r] = score;
g[l][r] = k;
}
}
}
}
cout << f[1][n] << endl;
dfs(1, n);
return 0;
}
