一、题目

给定长度为 $N$ 的序列 $A$，构造一个长度为 $N$ 的序列 $B$，满足：

1.$B$ 非严格单调，即 $B_1≤B_2≤…≤B_N$ 或 $B_1≥B_2≥…≥B_N$。
2.最小化 $S=∑^N_{i=1}|A_i−B_i|$。

只需要求出这个最小值 $S$。

输入格式

第一行包含一个整数 $N$。

接下来 $N$ 行，每行包含一个整数 $A_i$。

输出格式

输出一个整数，表示最小 $S$ 值。

数据范围

$1≤N≤2000$,
$0≤A_i≤10^9$

输入样例：

7
1
3
2
4
5
3
9

输出样例：

3

二、分析

此题有个结论：$B_i$ 一定为序列 $A$ 中的某个数字。

证明：

假设某个最优解序列如下图所示， $A_i$ 为 原序列， $A_i’$ 为将原序列按从小到大排序后的序列。红点为 $B$ 序列的分布。显然，每个 $B_i$ 一定要么等于某个 $A_i$ 或者不等于任何 $A_i$ ，假设存在若干个 $B_i$ 介于$A’_ i$ 和 $A’_ {i+1}$ 之间，即不等于任何 $A_i$，如图中粉色框框所示。假设这些 $B_i$ 所对应的 $A_i$ 的值 有x个值小于等于 $A’_ i$ ，有 y个值大于等于 $A’_ {i+1}$ ,分三种情况进行构造：

• x > y ,说明如果将粉色框整体向下移动，直到最小的红点等于 $A’_ i$ ，此操作保证使整体结果更优。
• x < y，则整体向上移动，使得最大的等于 $A’_ {i+1}$，可以使得总和变小。
• x == y ，则上移下移都一样，总和不会改变。

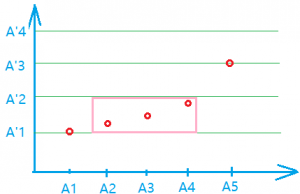
按照上述构造方法，可以将所有不在 $A’_ i$ 上的点移动到某个 $A_i’$ 上，证毕。

上面对于构造方法的解释可能不太清晰，以下图为例，假设有$A_ 1$，$A_ 2$都小于 $A’_ 1$ , $A_ 3$ 大于$A’_ 2$ , 即 x > y ，则将三个红点都向下移动等长的距离，直到最下面的红点碰到 $A’_ 1$ 为止。则 $|A_1−B_1|$ 和 $|A_2−B_2|$ 都变小了， 虽然 $|A_3−B_3|$ 变大了，但是整体还是更优，所以这是一种合理的构造方式。

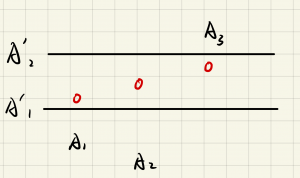
利用这个结论我们可以用动态规划的思想：

$dp[i][j]$ 表示已经考虑前 $i$ 个 $b_i$ 且最后一个以 $a_j$ 结尾的最优解，则$dp[i][j] = min(dp[i-1][k]) + abs(a[i] – b[j]), 1 <= k <= j$， 其中 $a[i]$ 存原数组， $b[j]$ 存a数字排序后的数组，由于要满足 $b_i <= b_{i+1}$ （这里只考虑单调递增，单调递减就是反着再求一遍就行），所以 $k$ 枚举下标 $1-j$ 的所有可能，取最优解即可，这里需要 $O(n)$ 。但是 $j$ 每次是加一的，所以维护一个 1 到 j 的最小值，类似前缀和思想，可以将整个算法时间复杂度优化到 $O(n)$ 。

三、代码

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
LL dp[3333][3333], a[3333], b[3333];
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
    sort(b + 1, b + 1 + n);
    for (int i = 1; i <= n; i++) {
        LL mmin = 1e18;//表示只考虑i-1个元素，结尾元素为b中的下标为1到j的最优解
        for (int j = 1; j <= n; j++) {
            mmin = min(mmin, dp[i - 1][j]);//先更新一下最优解
            dp[i][j] = mmin + abs(a[i] - b[j]);//dp[i][j] 就是只考虑前i-1种元素的最优解加上当前这个的abs
        }
    }
    LL ans = 1e18;
    for(int i = 1; i <= n; i++) ans = min(ans, dp[n][i]);
    sort(b+1,b+1+n,greater<int>());//按照升序再来一次
    for(int i = 1; i <= n; i++) {
        LL mmin = 1e18;
        for(int j = 1; j <= n; j++) {
            mmin = min(mmin, dp[i-1][j]);
            dp[i][j] = mmin + abs(a[i] - b[j]);
        }
    }
    for (int i = 1; i <= n; i++) ans = min(ans, dp[n][i]);
    cout << ans;
}