题目链接

A. Eshag Loves Big Arrays

题意

给你一个数列，你有一种操作：每次选择任意个数字，然后将其中严格大于平均值的数删去，其中平均值指的是你所选数字的平均值。问你可以删去的数字的最大数量，可以进行无限次操作。

分析

两个数相加后的平时值一定小于较大的数，或者说对于一堆较大的数，如果再加入一个较小的数，那么平均值一定小于较大的数，且无论较大的数有几个，所以最后数列里最小的数都无法删去，删去的数就是最大数量。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5+10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int,int> PII;
typedef pair<LL,LL> PLL;
int tong[1111];
int main(int argc, char const *argv[]) {
    int t;
    cin >> t;
    while(t--) {
        memset(tong,0,sizeof tong);
        int n;
        cin >> n;
        for(int i = 0; i < n; i++) {
            int x;
            cin >> x;
            tong[x]++;
        }
        int pos;
        for(int i = 1; i <= 100; i++) {
            if(tong[i] != 0) {
                pos = i;
                break;
            }
        }
        cout << n - tong[pos] <<endl;
    }
    return 0;
}

B. Sifid and Strange Subsequences（贪心）

题意

给你一个数列，要求你选出最多的数字，并且使得选出的数列陌生，陌生的定义为：任意两个数的差值的绝对值大于等于整个数列的最大值。

分析

一开始就想到负数肯定是毋庸置疑要选择的，于是决定排个序，排完序后感觉从小到大选择数字就是最优的。其实，两个正数的差值一定小于较大的正数，所以最多只能选一个正数，当然也可能一个正数都不能选，所以从小到大逐个选，直到不符合条件就退出。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
LL a[maxn];
int main(int argc, char const *argv[]) {
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        for (int i = 0; i < n; i++) scanf("%lld", a + i);
        sort(a, a + n);
        int i = 1;
        LL mmin = 0x3f3f3f3f3f3f3f3f;
        for (; i < n; i++) {
            mmin = min(mmin, abs(a[i] - a[i - 1]));
            if (mmin < a[i]) break;
        }
        //puts("-------------");
        cout << i << endl;
    }
    return 0;
}

C. Parsa’s Humongous Tree(树形DP)

题意

给你一颗树，每个点有一个取值范围，要求你给每个点选择一个权值，使得边权和最大，每条边的边权就是两个端点的差的绝对值。

分析

首先很关键的一点就是要分析出，每个点的取值其实就最大值或者最小值，因为边权是两个端点的差值，所以两个端点的值相差越大那么边权越大，证明如下：设有三个点a,b,c，a和b连，b和c连，a和c的值固定为x和z，如果b的值取y，那么权值和为abs(x-y) +abs(z-y),分三种情况讨论：

• x<y且z<y，那么将y+1可以使得权值和+2
• x>y且z>y，那么将y-1可以使得权值和+2
• x<y<z或z<y<x，将y+1或者y-1，权值和不变

综上所述，y取一个最极端的情况可以使得权值更大。

所以设 $dp[x][0/1]$ 表示以x为根的子树的边权和，其中0表示x取最小值，1表示x取最大值，跑个dfs，处理出所有子节点的dp值后在回溯的时候将根节点的dp值进行更新，注意更新的时候不一定是根节点最小值和子节点是最大值之间差值更大，也可能是根节点最小值和子节点的最小值相差更大，如（根节点范围为3-4，子节点为1-3，当根节点选最小值时，子节点选择最小值两者的差值更大），所以dp更新的时候需要两种情况取一个max。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int n, cnt, h[maxn], to[maxn], ne[maxn], vis[maxn];
LL L[maxn], R[maxn], dp[maxn][2];
void add(int a, int b) {
    to[cnt] = b;
    ne[cnt] = h[a];
    h[a] = cnt++;
}

void dfs(int x) {
    for (int i = h[x]; ~i; i = ne[i]) {
        int y = to[i];
        if (vis[y]) continue;
        vis[y] = 1;
        dfs(y);//先向下算好子节点的值，再自底向上更新dp值
        //计算x取最大值时的最优解，注意x取最大值，y可能取最大也可能取最小值
        dp[x][1] += max(dp[y][0] + abs(R[x] - L[y]),dp[y][1] + abs(R[x] - R[y]));
        //计算x取最小值的最优解，同上
        dp[x][0] += max(dp[y][0] + abs(L[x] - L[y]),dp[y][1] + abs(L[x] - R[y]));
    }
}

int main(int argc, char const *argv[]) {
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        memset(vis, 0, sizeof vis);
        memset(dp, 0, sizeof dp);
        memset(h, -1, sizeof h);
        cnt = 0;
        for (int i = 1; i <= n; i++) scanf("%lld %lld", L + i, R + i);
        for (int i = 0; i < n - 1; i++) {
            int x, y;
            scanf("%d %d", &x, &y);
            add(x, y);
            add(y, x);
        }
        vis[1] = 1;
        dfs(1);
        //puts("------");
        cout << max(dp[1][0], dp[1][1]) << endl;
    }
    return 0;
}

D. Kavi on Pairing Duty（DP）

题意

给你2n个点，让你找出所有的组合个数，每个组合中要求所有的点都两两连线构成一个匹配，任意两个匹配要求满足一下两个要求之一：

• 两个匹配的长度相同
• 一个匹配将另外一个匹配包含在内

如下图，A和B都是一个组合，而C不是，问你2n个点能构成几个不同的组合。

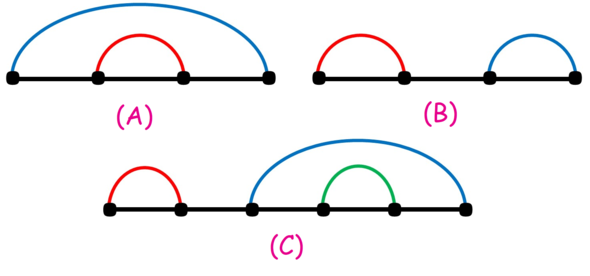
分析

此题暴力肯定不行，考虑使用DP，那么第一个问题就是如何划分状态使得不重不漏，以n=4为例，首先看下面的几种情况：

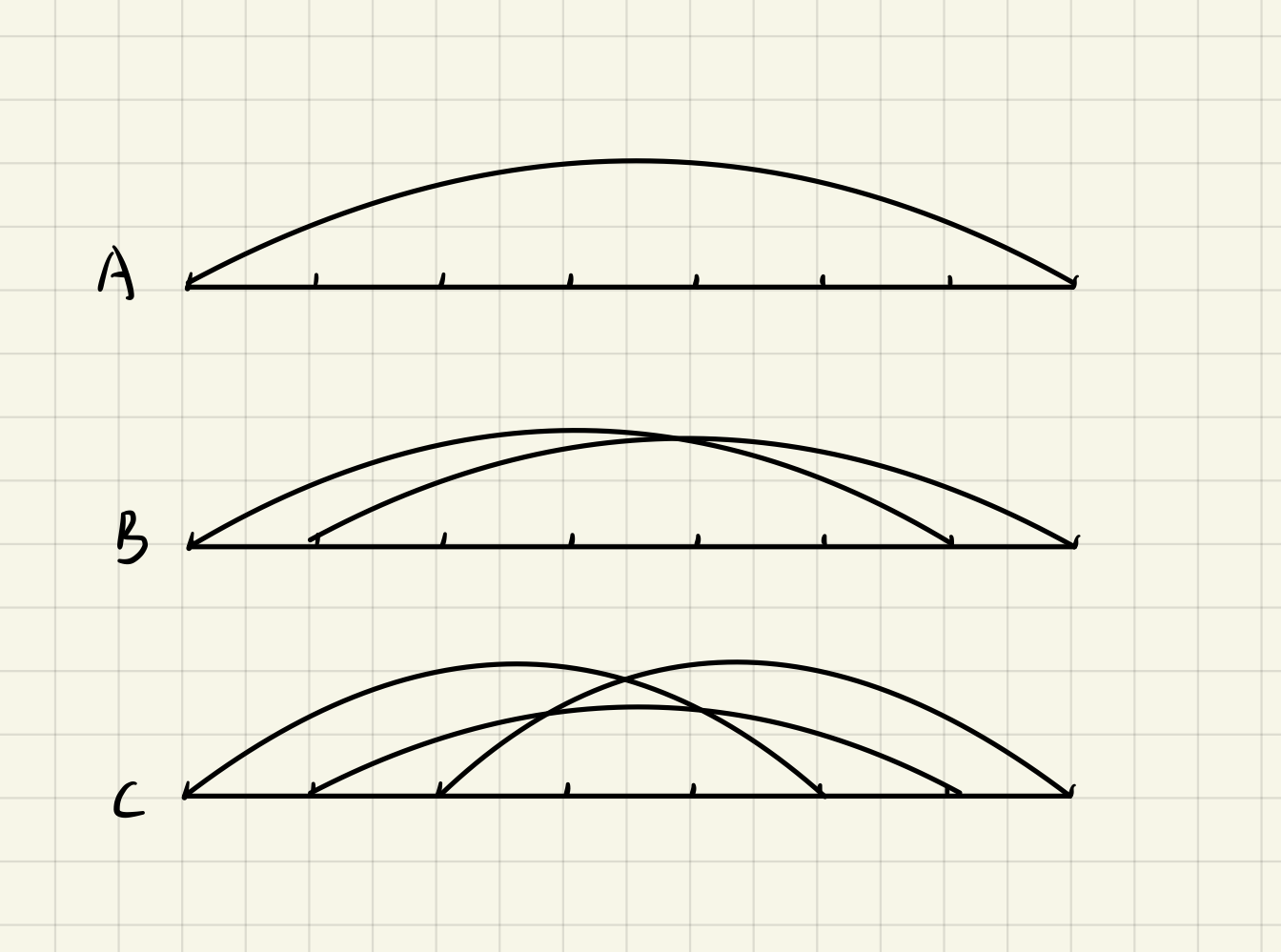
可以发现：

• 图A这种情况可以得到的组合个数其实就是n=3时的组合数；

• 图B这种情况可以得到的组合个数其实就是n=2时的组合数；

• 图C这种情况可以得到的组合个数其实就是n=1时的组合数；

再看下面这些情况：

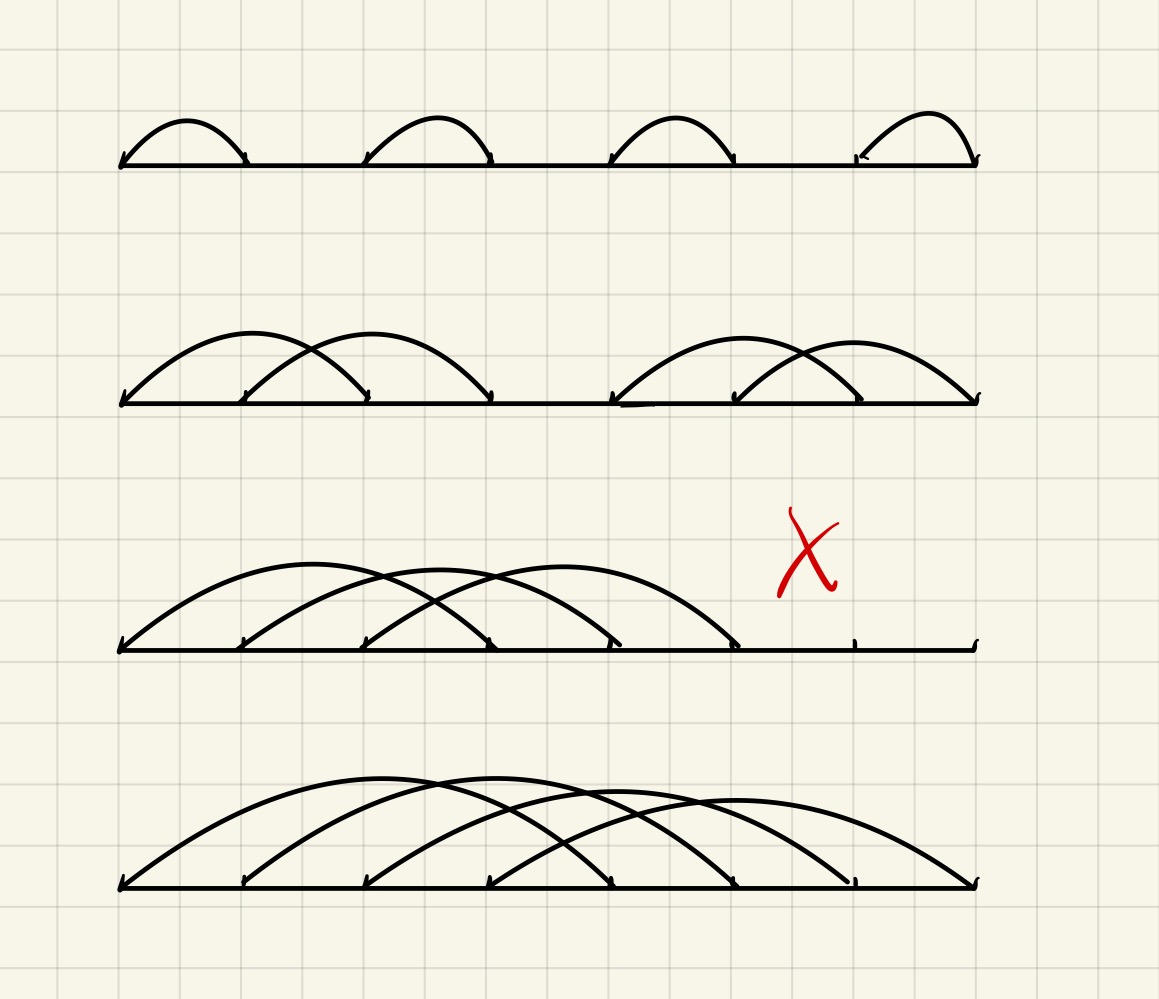
这类情况的特点是每个匹配的长度都相同，我们按照每个匹配的长度length来划分，发现length为1、2、4都是可以得到合法的组合的，而length为3时无法得到一个合法的组合。更一般化地去讨论我们可以发现，每个组合内可以分成一样的几套匹配，如图所示，length为2的两个匹配作为一套，有2套，每套4个点；length为3的三个匹配作为一套，6个点，但是不合法；length为4的四个匹配作为一套，有1套，每套8个点。所以只要总点数可以被每套的点数整除，那么就是一种合法方案。所以对于总点数为x的情况，所有匹配的长度相同的组合数就是x的所有偶数因子的个数（不包括2，因为一套最小点数为4个），再加上1（length为1的情况）。

综上，设$dp[i]$表示 n = i 时的组合个数，则 $dp[i] = \displaystyle \sum_{j = 1}^{i-1} dp[j] +fa[i*2]$ ，其中fa表示组合中每个匹配长度都相同的组合个数。

题目要求的是n的组合个数，对于dp值的更新很简单，我们可以从1开始递推下去，用一个变量维护前缀和，每次更新都是$O(1)$，整体为$O(n)$，fa数组只要用倍数法预处理一遍即可，注意枚举因子的时候从4开始枚举，并且只枚举偶数因子，并在最后给每个fa的值都+1（length为1的情况），预处理的时间复杂度为$O(nlogn)$。

代码

#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 4e6 + 10;
const int mod = 998244353;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int fa[maxn];
void Init() {
    for (int i = 4; i < maxn; i += 2)//从4开始枚举所有的偶数因子
        for (int j = 1; j * i < maxn; j++) {
            fa[i * j]++;
        }
    for (int i = 2; i < maxn; i += 2) fa[i]++;//加上length为1的情况
}
LL dp[maxn];
int main(int argc, char const *argv[]) {
    Init();
    int n;
    cin >> n;
    dp[1] = 1;
    LL sum = 1;//前缀和
    for (int i = 2; i <= n; i++) {
        dp[i] = (sum + fa[i * 2]) % mod;
        sum = (dp[i] + sum) % mod;
    }
    cout << dp[n] << endl;
    return 0;
}