A. Stone Game
题意
n个石子排成一排,每个石子有一个能力值,且每个石子的能力值各不相同,每次可以销毁最左边的石子或者最右边的石子,问最少几次消除能力值最大和最小的石子。
分析
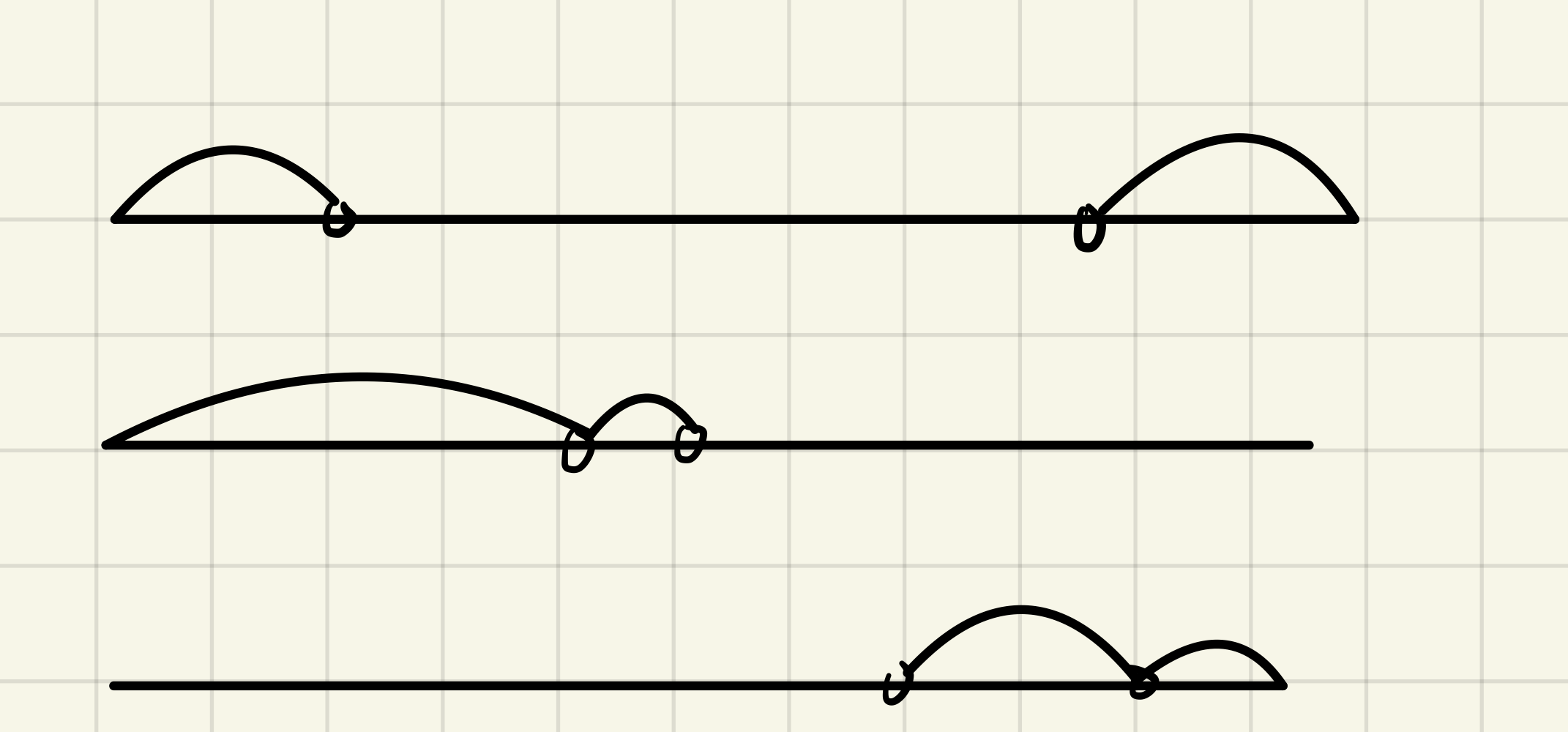
如图一共有这三种可能的删除方式,都算一下取最优解即可。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5+10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int,int> PII;
typedef pair<LL,LL> PLL;
int a[1111];
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while(t--) {
int n;
cin >> n;
int p1,p2,m1 = inf,m2 = -inf;
for(int i = 0; i < n; i++) {
cin >> a[i];
if(m1 > a[i]) {
m1 = a[i];
p1 = i;
}
if(m2 < a[i]) {
m2 = a[i];
p2 = i;
}
}
if(p1 > p2) swap(p1,p2);
int ans;
ans = min(p1+1+n-p2,min(p2+1,n-p1));
//puts("--------");
cout << ans << endl;
}
return 0;
}
B. Friends and Candies
题意
有n个朋友,每个朋友有 $a_i$ 个糖果,你可以进行一次操作:随意选取 $k$ 个人,然后将这 $k$ 个人的糖果任你分配给所有人。要求你选最小的 $k$ 使得每个人的糖果一样多。
分析
首先如果平均数不为整数,则不能分配,其余情况一定有解。为了每个人的糖果一样多,只要将大于平均数的分配给小于平均数的即可,并且大于平均数的是一定会被选择的,所以只要统计有几个人大于平均值即可。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 2e5+10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int,int> PII;
typedef pair<LL,LL> PLL;
int a[maxn];
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while(t--) {
int n;
cin >> n;
LL sum = 0;
for(int i = 0; i < n; i++){
scanf("%d",a+i);
sum += a[i];
}
if(sum % n != 0) puts("-1");
else {
LL ave = sum / n;
int ans = 0;
for(int i = 0; i < n; i++) {
if(a[i] > ave) ans++;
}
cout << ans <<endl;
}
}
return 0;
}
C. Number of Pairs
题意
给你一个数组a,让你找到所有的pair(i,j) 的个数,满足 $l \le a_i + a_j \le r (1 \le i < j \le n)$,l,r为题目给出的数。
分析
首先可以想到先排个序,虽然题目要求 $i<j$, 但是并没有规定 $a_i$ 和 $a_j$ 的大小,所以可以打乱顺序。暴力是 $O(n^2)$,不行,但是我们可以发现一个特性:从小到大排好序后,如果 $a_i + a_j \ge l$ 那么 $a_i + a_{j+1} \ge l$ 也是满足的 ,并且如果 $a_i + a_j > r$ 那么 $a_i + a_{j+1} > r$ 也是满足的,所以我们从最大值开始向下找到最小的L,满足$a_i + a_L \ge l$,然后在找到最大的 R,满足 $a_i + a_R \le r$ ,那么对于$a_i$ 可以配对的个数就是 R-L+1 个。接着对于 $a_{i+1}$ 我们只要从原来的L和R开始继续往左找,找到最小的L和最大的R,再统计个数,直到统计完全部。需要注意的是,为了防止重复统计,对于每个 $a_i$ 的 L ,L的值是要大于 i 的,整个时间复杂度为 $O(n)$。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 2e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int a[maxn];
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
int n, l, r;
cin >> n >> l >> r;
for (int i = 0; i < n; i++) {
scanf("%d", a + i);
}
sort(a, a + n);
int L = n, R = n-1;
LL ans = 0;
for (int i = 0; i < n - 1; i++) {
L = max(L,i+1);
while (L - 1 > i && a[L - 1] + a[i] >= l) L--;
while (R >= L && a[R] + a[i] > r) R--;
if (R < L || a[i] + a[L] < l || a[i] + a[R] > r) continue;
ans += R - L + 1;
}
cout << ans << endl;
}
return 0;
}
D. Another Problem About Dividing Numbers
题意
给你两个正整数a,b,每一次你可以任选一个大于1的正整数c,然后进行下列操作之一:
- 将a变成a/c,且必须满足 a % c = 0;
- 将b变成b/c,且必须满足 b % c = 0;
问你是否可以通过k次操作使得a和b的值相同。
分析
将两个数分别质因数分解,则可以进行的操作的最大次数为两个数的质因数的个数之和。如:$36 = 2 ^ 2 * 3 ^2, 48 = 2^4*3$,则两个数的最多操作次数为 2+2+4+1 = 9 次。对于最小操作次数需要进行分类讨论:
- a = = b时,最小操作次数为0。
- a可以被b整除或者b可以被a整除时,最小操作次数为1。
- 其余情况都为2次。
需要注意的是,如果a = = b时,k不能为1,因为不能通过一次操作使得两者相等,然后只要判断一下k是否介于最大值和最小值之间即可。
这题恶心人的地方是卡常数,如果用longlong会T6;如果质因数分解时使用for (int i = 2; i <= x / i ; i++) 也会T6,而使用for (int i = 2; i * i <= x ; i++)就可以过,因为除法速度较慢。但同时,for (int i = 2; i * i <= x ; i++) 这种写法 i 会有爆int的风险(虽然此题不会),故以后最保险的做法是先定义一个变量 n = sqrt(x) 。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5+10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int,int> PII;
typedef pair<LL,LL> PLL;
int divide(int x) {
int res = 0;
for (int i = 2; i * i <= x ; i++)
if (x % i == 0) {
int s = 0;
while (x % i == 0) x /= i, s++;
res += s;
}
if (x > 1) res++;
return res;
}
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while(t--) {
LL a, b, k;
cin >> a >> b >> k;
int mmax = divide(a) + divide(b);
int mmin;
if(a == b) mmin = 0;
else if(a % b == 0 || b % a == 0) mmin = 1;
else mmin = 2;
if(a == b) {
if(k == 0 || (k >= 2 && k <= mmax)) puts("YES");
else puts("NO");
continue;
}
if(k >= mmin && k <= mmax) puts("YES");
else puts("NO");
}
return 0;
}
E. Funny Substrings
题意
现有两种操作:
- 将变量x赋值为s,其中s为字符串。
- 将a+b的值赋给x,其中a和b为变量名,+表示字符串首尾相连。
问你经过n次操作后,字符串中有几个”haha”,题目保证每次赋值的字符串长度和变量名的长度小于5。
分析
暴力不行,字符串很长。我们发现,每个初始的字符串都很小,而两个字符串相连时只有连接处可能会产生新的”haha”。我们定义一个结构体,记录每个变量的:前三个字母(head)、后三个字母(tail)、字符串长度(size)、当前字符串中有几个”haha”(cnt)。设有两个上述的结构体a和b,那么当这两个结构体代表的变量相连时,产生的新结构体c的信息维护方式如下:
c.size= a.size + b.size;c.cnt = a.cnt + b.cnt + plus,其中plus表示由于连接产生的新的”haha”的个数,即计算一下a的后缀和b的前缀相连形成的字符串中有几个haha。c.head = a.head,这里要注意如果a不足3个,还要算上一部分的b的前缀,注意特判a和b的个数加起来都小于3的情况。c.tail = b.tail,注意如果b不足3个,还要加上a的部分后缀。
之所以只维护三个字母是因为,最多在连接处左右3个字符之间会产生新的”haha”,可以举例子反证一下。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
unordered_map<string, int> mp;
struct node {
string head, tail;
LL size;
LL cnt;
};
vector<node> ku;
int cal(string s) {
if (s.size() < 4) return 0;
int res = 0;
for (int i = 0; i <= s.size() - 4; i++) {
if (s.substr(i, 4) == "haha") res++;
}
return res;
}
void merage(string a, string b, string c) {
node x = ku[mp[b]];
node y = ku[mp[c]];
node temp;
if (x.size + y.size < 3) temp.head = temp.tail = x.head + y.head;
else {
if (x.size >= 3) temp.head = x.head;
else temp.head = x.head + y.head.substr(0, 3 - x.head.size());
if (y.size >= 3) temp.tail = y.tail;
else temp.tail = x.tail.substr(y.tail.size() - (3 - y.tail.size()), 3 - y.tail.size()) +y.tail;
}
temp.size = x.size + y.size;
temp.cnt = x.cnt + y.cnt + cal(x.tail + y.head);
ku.push_back(temp);
mp[a] = ku.size() - 1;
}
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
string a, op, c, b;
cin >> a >> op >> b;
node temp;
if (op == ":=") {
temp.cnt = cal(b);
temp.size = b.size();
if (b.size() < 3) {
temp.head = b;
temp.tail = b;
} else {
temp.head = b.substr(0, 3);
temp.tail = b.substr(b.size() - 3, 3);
}
ku.push_back(temp);
mp[a] = ku.size() - 1;
} else {
cin >> op >> c;
merage(a, b, c);
}
if (i == n) cout << ku[mp[a]].cnt << endl;
}
}
return 0;
}
F. Interesting Function
题意
问你从 $l$ 一直+1直到 $r$ 的过程中每位的变化次数和,如 909 到 910 变化了两次, 489999到490000变化了5次。
分析
首先我们可以发现,如果要让各位+1,则总变化次数加1次,十位上+1;则变化次数加11次;百位+1,变化次数加111次;所以我们从最低位向高位依次考虑即可。注意如果a的某位大于b,则需要进位操作,需要统计一下由于进位造成的位数变化次数,并将a的值更新。
代码
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
int cal(LL a, LL b) {//计算由于进位产生的位数变化次数
int res = 0;
while(a && b) {
if(a %10 != b % 10)
res ++;
a /= 10, b /= 10;
}
while(b) res++,b/=10;
return res;
}
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
int l, r;
cin >> l >> r;
LL wei = 1;
LL ans = 0;
while (l) {
int a = l % 10, b = r % 10;
l /= 10, r /= 10;
if (a > b) {//需要进位
//前半部分是计算将a的这一位变成和b相同的过程中位数变化了几次,后半部分计算由于进位产生的位数变化。
ans += (LL)(10 - a + b) * wei + cal(l,l+1);
l++;//将l的值更新
} else
ans += (LL)(b - a) * wei;
wei = wei * 10 + 1;
}
while (r) {
ans += (LL)(r % 10) * wei;
wei = wei * 10 + 1;
r /= 10;
}
cout << ans << endl;
}
return 0;
}
G. Gift Set
题意
有x个红糖果和y个蓝糖果,你可以将a个红糖果和b个蓝糖果打包成一个礼物盒,或者将b个红糖果和a个蓝糖果打包成一个礼物盒,问你最多可以组成几个礼物盒。
分析
此题可以二分也可以三分来做。先说二分做法:
设可以分成n个礼物盒,其中方案一有s个,方案二有t个,为了方便,假设(a<b,x<y),可以得到:
代换、移项后可得:
其中,x,y,a,b为已知值,二分查找n,check上述不等式是否合法。
下面是三分做法:
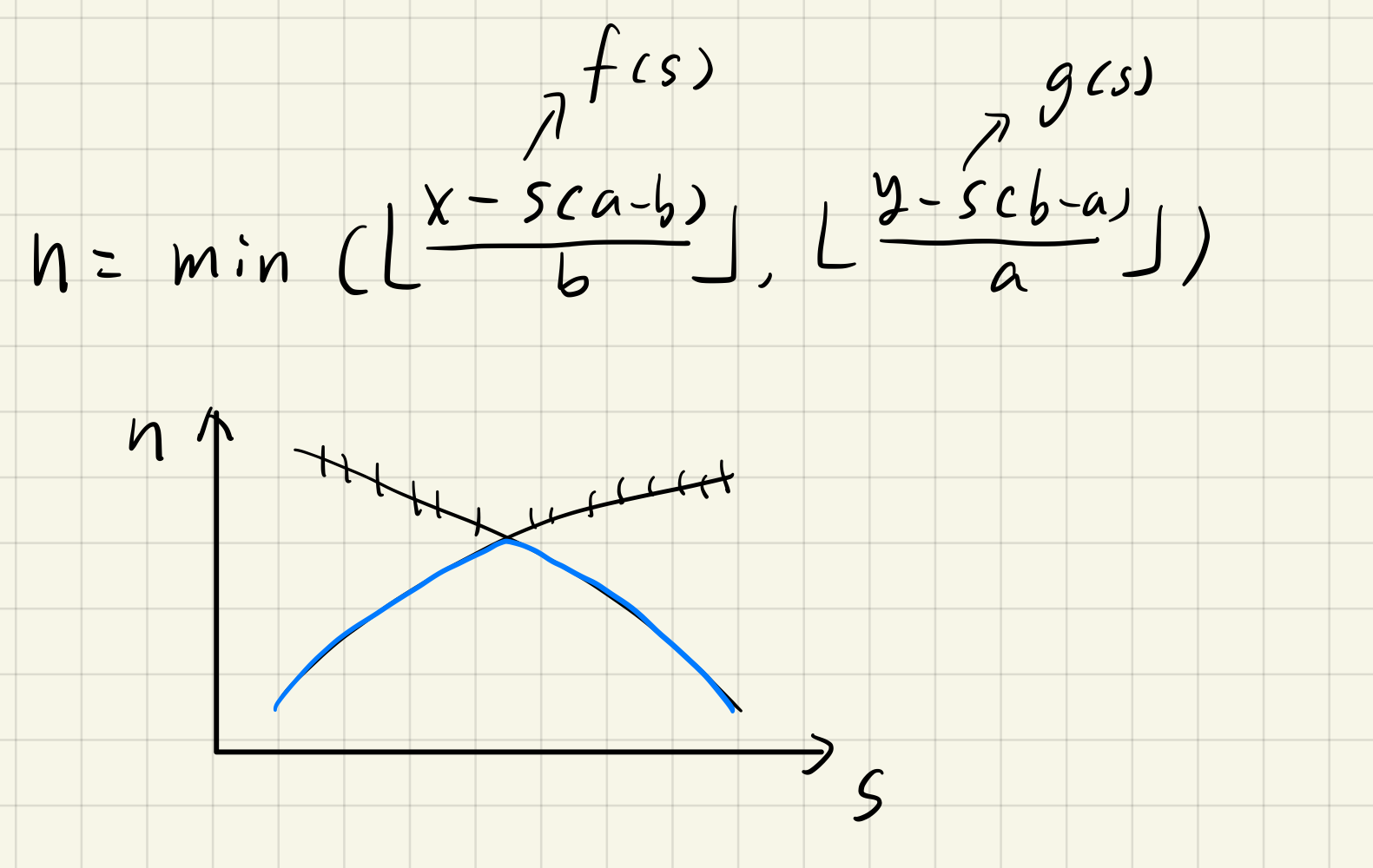
如上图,n表示总礼盒数,s表示方案一的个数,那么就可以通过总数算出方案二的个数,然后就能算出总礼盒数n,公式如上图。那么可知 $f(s)$ 和 $g(s)$ 的单调性相反,取两者的最小值,很容易得到,自变量为s,应变量为n的函数是一个单峰函数,满足三分的性质。每次取两个点,计算这两个点的n,然后相应变化指针即可。
有两个注意点,要用double来三分,因为如果用int三分,对于取值一样的n是无法正确变化指针的。double三分后得到的值是个double数,要向左和向右枚举几次求一下最大值,具体看代码。
代码
二分版本:
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
LL x, y, a, b, ans;
bool check(LL mid) {
LL l;
if (l - mid * b >= 0)
l = 0;
else {
l = (mid * b - x + b - a - 1) / (b - a);
}
LL r = ((y - mid * a) * 1.0 / (b - a));
return max(l, 0LL) <= min(r, mid);
}
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
ans = -1;
cin >> x >> y >> a >> b;
if (x > y) swap(x, y);
LL l = 0, r = x;
if (a > b) swap(a, b);
if (a == b) {
cout << x / a << endl;
continue;
}
while (l <= r) {
LL mid = (l + r) >> 1;
if (check(mid)) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
cout << ans << endl;
}
return 0;
}
三分版本:
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int maxn = 1e6 + 10;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const double PI = acos(-1.0);
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
LL x, y, a, b, ans;
double check(LL mid) {
double res = mid;
double h1 = x - a * mid, h2 = y - b * mid;
res += min(h1 / b, h2 / a);
return res;
}
int main(int argc, char const *argv[]) {
int t;
cin >> t;
while (t--) {
ans = 0;
cin >> x >> y >> a >> b;
double l = 0, r = min(x/a,y/b);
if ((x < a || y < b) && (x < b || y < a)) {
puts("0");
continue;
}
while(r - l > eps) {
double lm = (l + r)/2, rm = (lm + r)/2;
// cout << "num: "<< lm << ' ' << rm <<endl;
double a = check(lm), b = check(rm);
if (a > b) {
r = rm;
} else {
l = lm;
}
}
for(int i = l - 10; i <= r+10;i++) {
if(i < 0) continue;
if(x - i * a < 0 || y -i * b < 0) continue;
ans = max(ans,i + min((x-i*a)/b,(y-i*b)/a));
}
cout << ans << endl;
}
return 0;
}
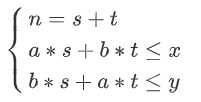
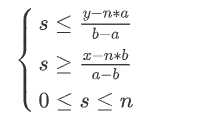

为什么D题在分解质因数时用$i≤x/i$会
TLE而用
long long两种写法都会TLE因为除法比乘法速度慢,涉及到硬件层面的知识。longlong63位,int32位,运算的时候也是int快一点,具体要看CPU和编译器。
原来这题这都卡,谢谢
究极卡常