一、优化目标

1.1 从逻辑回归模型开始

在介绍SVM之前，我们先从逻辑回归模型开始，我们知道，逻辑回归的假设函数为 $h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} x}}$，这就是一个Sigmoid函数，其图像如下图所示：

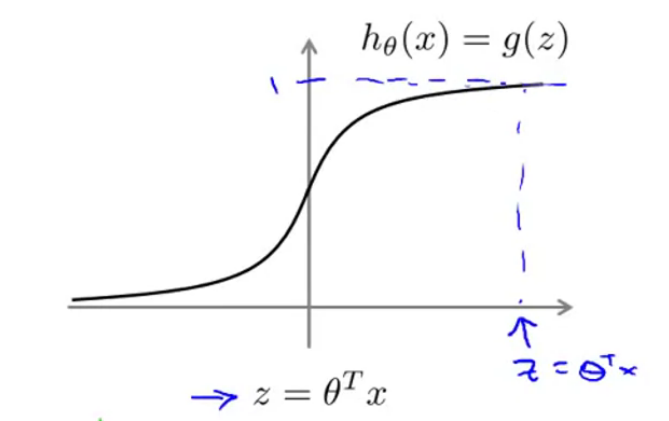
我们的目标是对于 $y=1$，希望 $h_{\theta}(x) \approx 1, \quad \theta^{T} x \gg 0$

对于 $y = 0$， 希望 $h_{\theta}(x) \approx 0, \quad \theta^{T} x \ll 0$

下面对逻辑回归的代价函数进行分析：

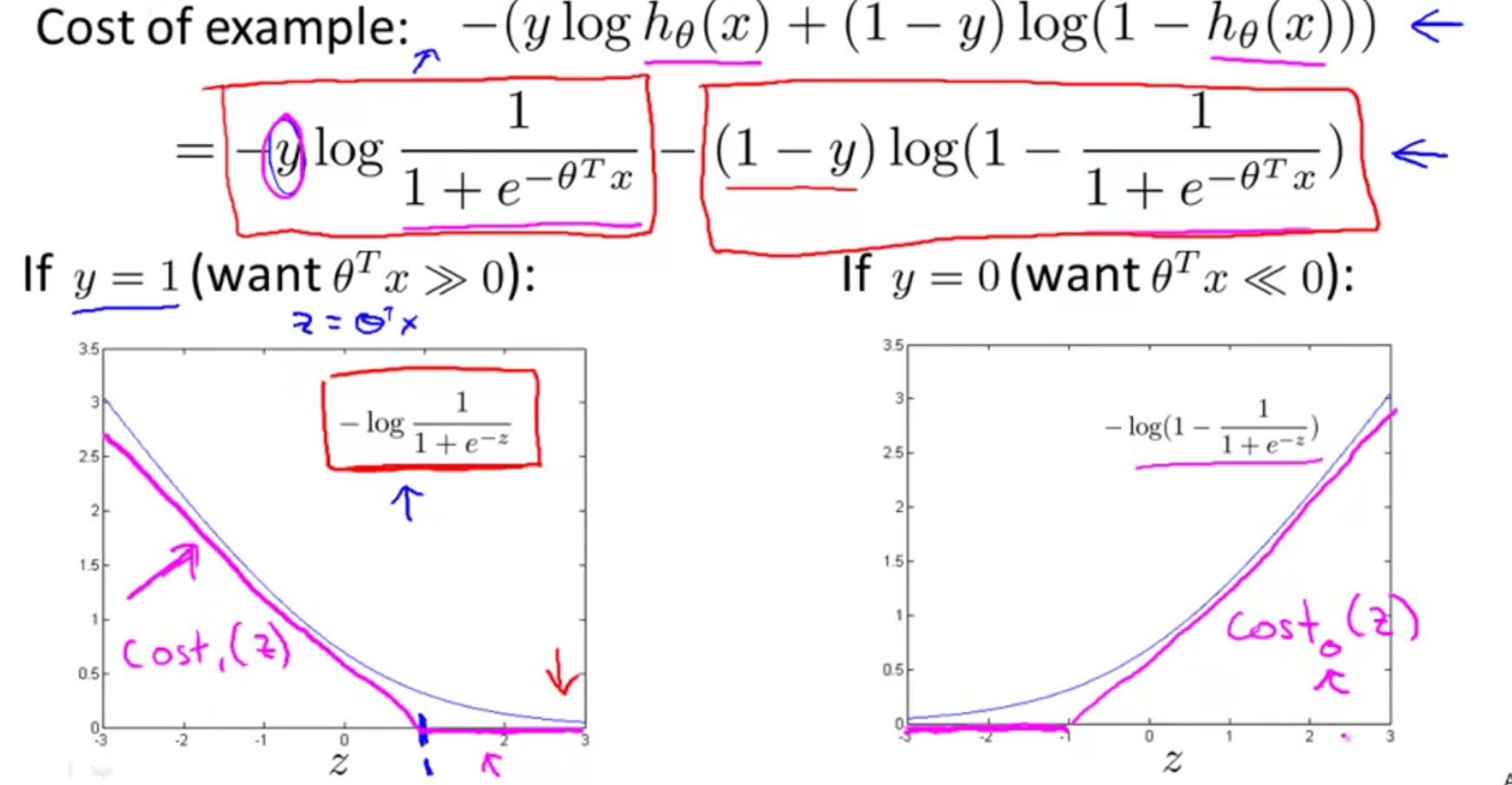
当 $y=1$ 时，代价函数变为 $-\log \frac{1}{1+e^{-z}}$，代价图像如上图左所示，我们的优化目标是使得代价函数尽量的小，在图中可以看出，当 $z = \theta^{T} x$ 尽量大的时候，代价函数就趋近于0，这和我们的真实目标相符合，即对于 $y=1$，希望 $h_{\theta}(x) \approx 1, \quad \theta^{T} x \gg 0$。同样对于，$y = 0$ 的情况也是如此，不重复分析。我们可以将代价函数图形化简，如上图粉红色的线段所示，化简后的代价函数用 $cost_1()$ 和 $cost_2()$ 表示。

1.2 SVM优化目标

对于逻辑回归的优化目标如下：

对于支持向量机的优化目标如下：

对比两个表达式，首先SVM的优化目标将参数 $m$ 删去，这是不重要的，因为这就是个常量，不会影响最优质的选取。直观来讲，对于一个函数乘上一个系数，只是将整个函数放大拉长了，最优解所在自变量的位置没变，只不过是函数值改变了。其次就是用新的代价函数 $cost_1$ 和 $cost_0$ 替换了逻辑回顾中的相应部分。此外将正则化系数 $\lambda$ 删去，而是在前面加入了一个系数 $C$ ，这对整个式子也是没有影响的，因为这些系数都是模型自己学习的，改变位置造成的效果可以看出，将 $C$ 考虑成 $\frac{1}{\lambda}$ 。注意这里说的只是效果上近似，并不是完全等价。比如 $\lambda$ 的作用是使得表达式前面一部分的值变小，那么 $\lambda$ 就要取一个较大的值 ，那么这和在前一部分乘上 $\frac1\lambda$ 效果是类似的。

最后有别于逻辑回归输出的概率，支持向量机所做的是它来直接预测y 的值等于1，还是等于0。因此，当$\theta^Tx \ge0$ 时，这个假设函数会预测1。

二、大边界分类器的理解

2.1 直观理解

人们有时也会将SVM称为大间距分类器，这里就来理解一下其中的原因。

如上图所示就是支持向量机的代价函数和图像，我们的目标是最小化代价函数。所以我们考虑一下最小化代价函数的必要是什么，假如现在有个正样本 $y=1$ ，那么代价函数就变成了上图左边的图像，观察图像可以发现，只有在 $z \ge 1$ 的时候代价函数最小为0。也就是说，当 $y=1$ 时，我们期望的是 $\theta^Tx \ge 1$ ，同理，当 $y = 0$ 时，我们期望 $\theta^Tx \le -1$ ，这和逻辑回归以 0 作为边界不同。支持向量机在正负类别之间空出了一个 $[-1,1]$ 的间隔，相当于在SVM中嵌入了一个额外的安全因子，或者说是一个安全的间距因子。

当 $C$ 设置地很大的时候，比如说100000，那么支持向量机的目标函数就可以写成：

对于这样的SVM模型，在如下图所示的数据中进行训练，通过数据分布可以看出这个数据是线性可分的，我们可以很轻松的用一条直线分开这两个数据集，如图中绿色和粉红的直线。但是当 $C$ 设置很大的时候，SVM会选择黑色的线作为决策边界，并且将黑线到正负样本之间的距离成为间距（margin），这也是SVM有很好的鲁棒性的原因，因为它一直努力用一个最大间距来分类样本，这也是SVM被称为大间距分类器的原因。至于为什么会选择黑线，在后面的数学解释中会介绍。

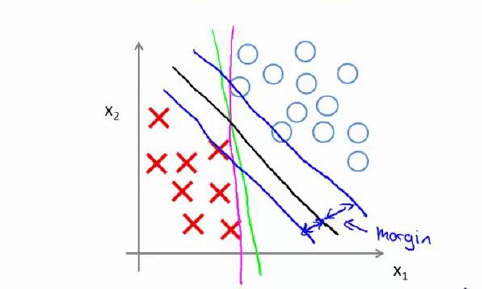
再来说一下SVM的正则化系数 $C$ ，考虑下面这样的数据分布，如果将 $C$ 设置很大，则很可能会得到粉线，如果将 $C$ 设置的不是非常大时，则可能得到黑线。

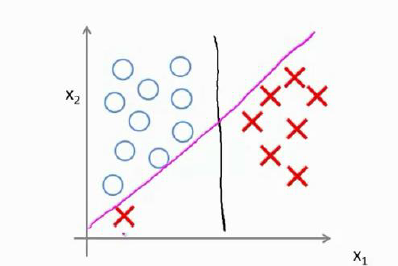
总结可以得到：

• C 较大时，相当于 λ 较小，可能会导致过拟合，高方差 。
• C较小时，相当于 λ 较大，可能会导致低拟合，高偏差。

2.2 数学解释

向量内积的回顾：

向量内积在几何意义上等于 投影 乘 被投影的向量长度，在坐标意义上等于对应坐标相乘再相加，用向量表示就是第一个向量的转置乘上第二个向量。

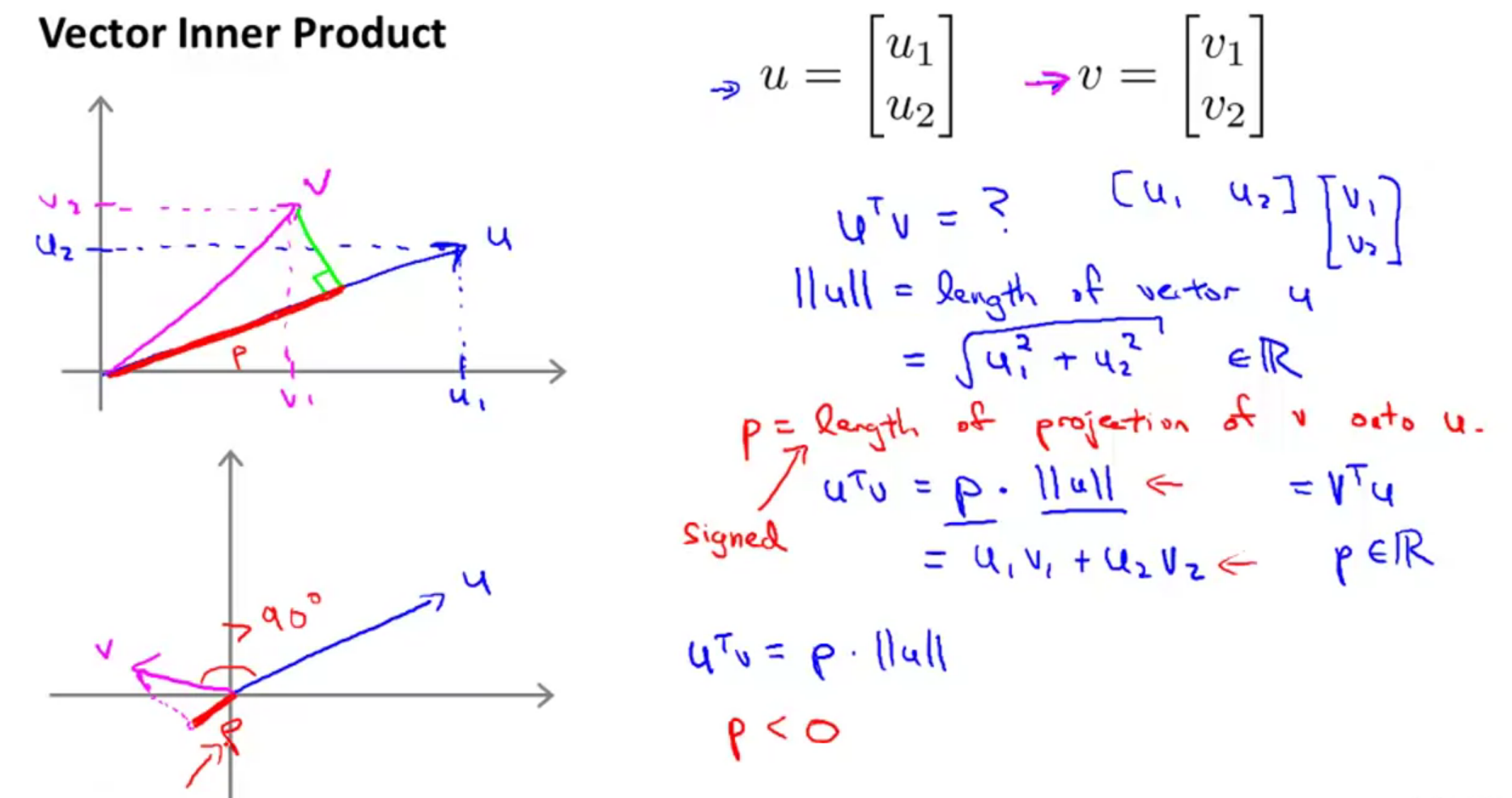
现在我们讨论的是 $C$ 很大的情形，并且为了简单起见我们假设 $\theta_0 = 0$ ，并且数据只有两个属性， 也就是说只有 $\theta_1$ 和 $\theta_2$，那么对于$C$ 很大的时候的SVM 的决策函数：

我们可以推得 $\frac{1}{2} \sum_{j=1}^{n} \theta_{j}^{2} = \frac{1}{2}\left(\theta_{1}^{2}+\theta_{2}^{2}\right)=\frac{1}{2}\left(\sqrt{\theta_{1}^{2}+\theta_{2}^{2}}\right)^{2}=\frac{1}{2}\|\theta\|^{2}$，由此我们就知道，优化目标是使得参数向量 $\theta$ 的范数最小，也就是长度最小。而对于约束条件 $\theta^Tx^{(i)}$ ，其实就是向量 $\theta$ 和向量 $x^{(i)}$ 的内积（因为第一个向量的转置乘上第二个向量就是向量的内积）。由于向量内积也有其几何意义，即 $\theta^{T} x^{(i)}=p^{(i)} \cdot\|\theta\|$，其中 $p^{(i)}$ 表示第 $i$ 个数据在向量 $\theta$ 上的投影。

于是，对于这样一个特殊的化简情况，我们就可以将目标函数写成：

对于下图的数据集，我们随意画了一条决策边界（绿色直线），由于$\theta$ 与决策边界垂直正交，所以我们可以画出 $\theta$ 的方向。至于为什么垂直，我们可以分别表示出决策边界和 $\theta$ 的斜率。由于决策边界上 $x_1\theta_1 + x_2\theta_2 = 0$ ，所以决策边界的斜率为 $-\frac{\theta_1}{\theta_2}$ ，由于向量 $\theta$ 过原点，所以斜率就是 $\frac{\theta_2}{\theta_1}$ ，相乘为-1，表示两直线垂直。

对于正样本，由于$p^{(i)}$ 表示在 $\theta$ 上的投影是一个定值，由于下图中的投影长度很短，所以要让 $p^{(i)}\|\theta\| \ge 1$ ，就必须要让 $\|\theta\|$ 很大，同样对于负样本，受制于约束条件，也会让$\|\theta\|$ 很大，这样的结果显然与目标函数（最小化 $\|\theta\|$ ）相悖。

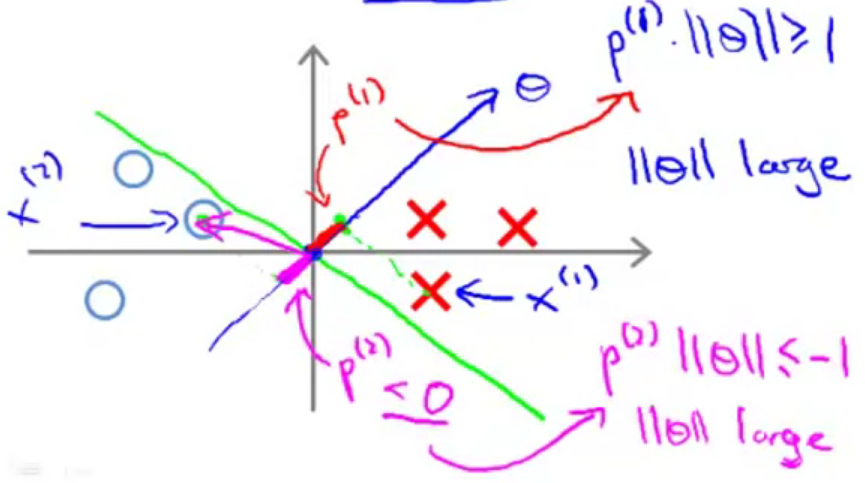
所以在目标函数的作用下，SVM会选择如下的决策边界，在这样的边界下，每个样本到 $\theta$ 的投影都尽量地大，使得 $\|\theta\|$ 就能尽量地小。

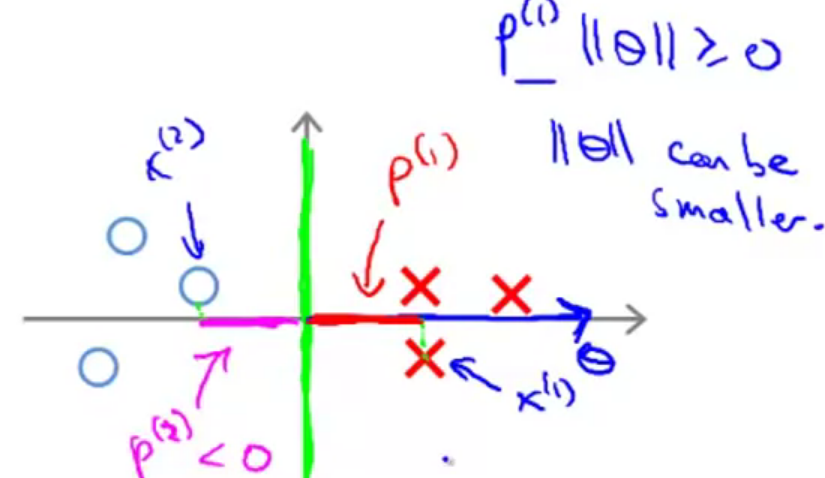
但需要注意的是，上述的推导都是基于 $\theta_0 = 0$ ，且特征只有两个的情况，如果 $\theta_0$ 不为0，则表示 $\theta$ 可以不过原点，特征增加，则表示在高维空间用超平面划分数据集，原理是相同的。

三、核函数

首先，先来回顾一下非线性回归问题分决策边界，如下图所示，通常情况下，对于一个非线性的问题，我们通过构造高次的特征项来解决。具体来说，我们的假设函数的定义能是当 $\theta_{0} +\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} x_{1} x_{2}+\theta_{4} x_{1}^{2}+\theta_{5} x_{2}^{2}+\cdots \geq 0$ 时，$y = 1$，反之等于0。

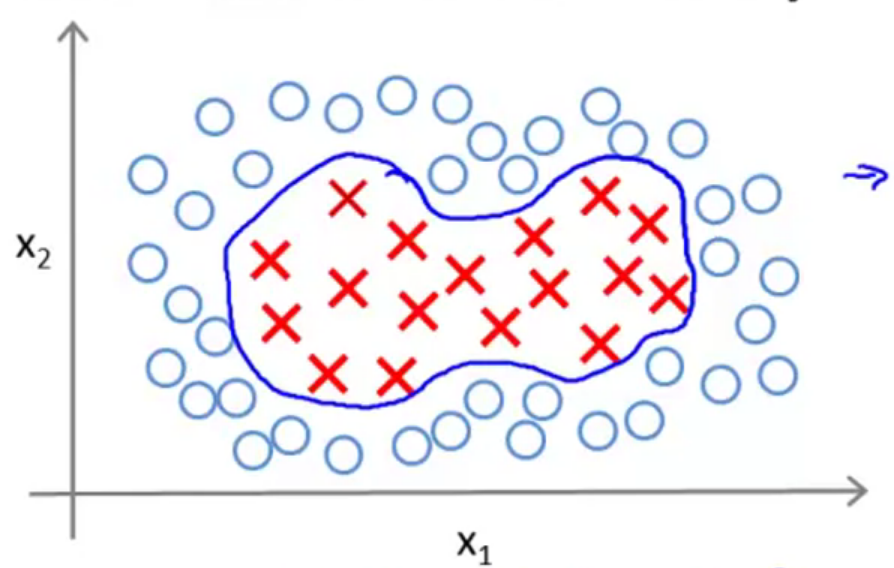
现在我们将假设函数换一种表示方法：$\theta_0 + \theta_1f_1+ \theta_2f_2+ \theta_3f_3...$，对于上面的式子，$f_1 = x_1, \ \ f_2 = x_2,\ \ f_3 = x_1x_2, \ \ f_4=x_1^2...$，那么除了无脑构造高次项，有没有更好的构造新特征的方式呢？有，那就是核函数。

3.1 高斯核函数

我们现在样本空间里随机取三个点，称为标记点（landmarks），分别标记为 $l^{(1)}l^{(2)}l^{(3)}$，如下图所示。

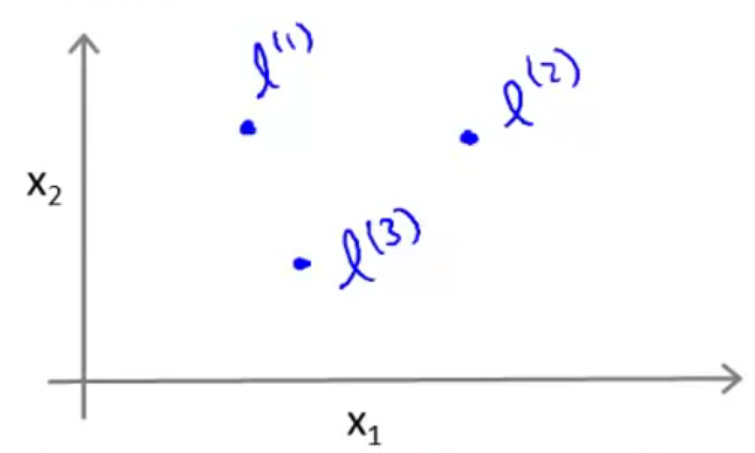
然后我们可以定义三个特征 $f_1 f_2 f_3$ ，其中 $f_1$ 的含义为某个样本与 $l^{(1)}$ 的相似度， $f_2$ 的含义为某个样本与 $l^{(2)}$ 的相似度，以此类推。对于 $f_1$ 其表达式为：

其余两个特征的定义类似，下面我们分析一下这个表达式：

• 当样本 $x$ 与 $l^{(1)}$ 很接近时，$\|x-l^{(1)}\|^{2}$ 约等于0，则 $f_1$ 约等于1。（exp表示 $e$ 的指数，$e^0=1$）
• 当样本 $x$ 与 $l^{(1)}$ 相差很多时，$\|x-l^{(1)}\|^{2}$ 为一个很大的数字，加上前面的负号，整体为一个很大的负数，则 $f_1$ 约等于0。

下面再来观察 $\sigma$ 对表达式的影响，假设 $l^{(1)}=\left[\begin{array}{l} 3 \\ 5 \end{array}\right]$，分别画出不同 $\sigma$ 值的图像，从而我们得出，$\sigma$ 控制着表达式的变化速度。

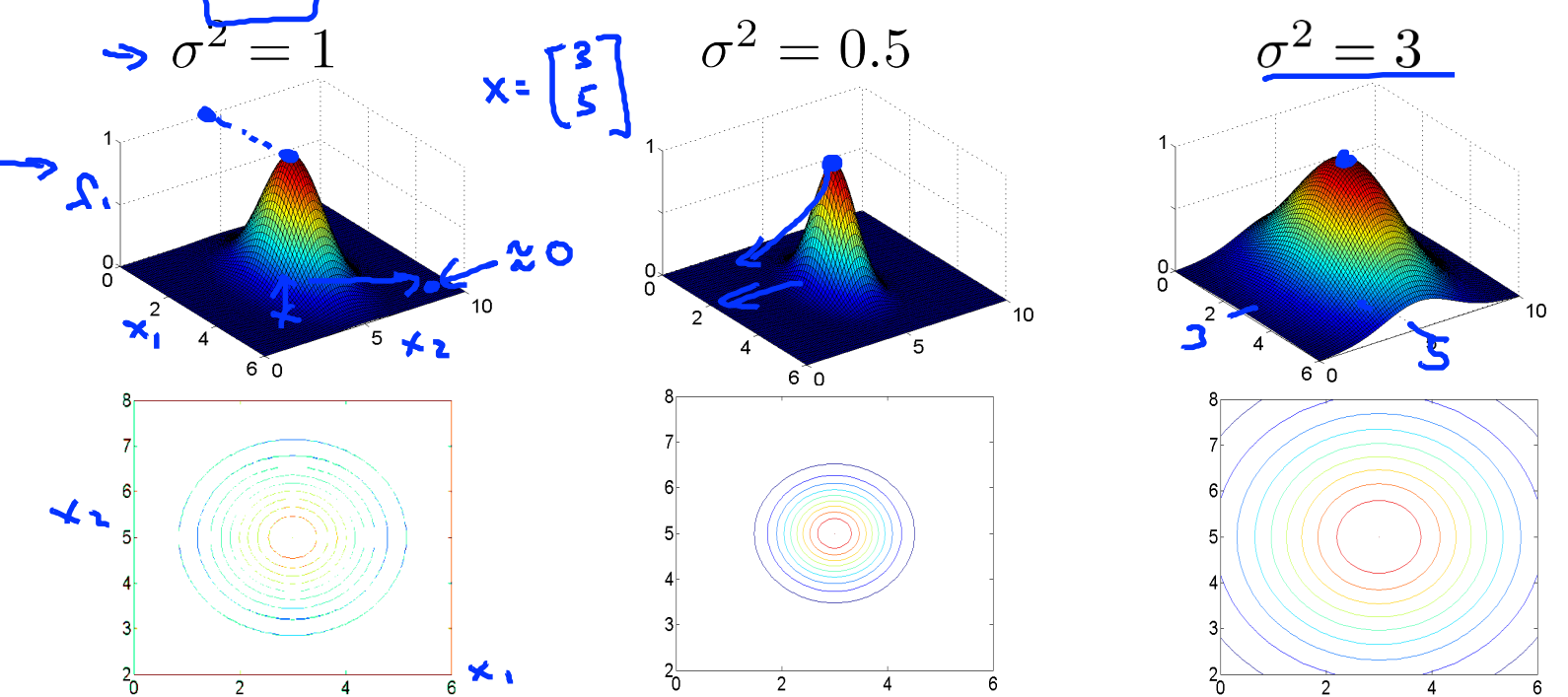
上面的这个表达式就是高斯核函数，那么使用高斯核函数为什么可以达到非线性的表达能力呢？可以看下面的例子：

假设我们的假设函数为 $\theta_0+\theta_1f_1 + \theta_2f_2+\theta_3f_3$ ，并且 $\theta$ 的取值如图中所示。对于图中红色的点，由于靠近 $l^{(1)}$ 远离 $l^{(2)}$ 和 $l^{(3)}$ ，而靠近 $l^{(i)}$ 则 $f_i$ 接近1，否则接近0，那么假设函数和可能就是一个正数，表示正类。而对于右下角的点，它远离三个 $l$ 点，则所有特征 $f$ 取值都为0，代入得结果为-0.5，表示负类。 最终能得道类似红色的决策边界（之所以 $l^{(3)}$ 被排除在外是因为它的权重 $\theta_3 = 0$）。

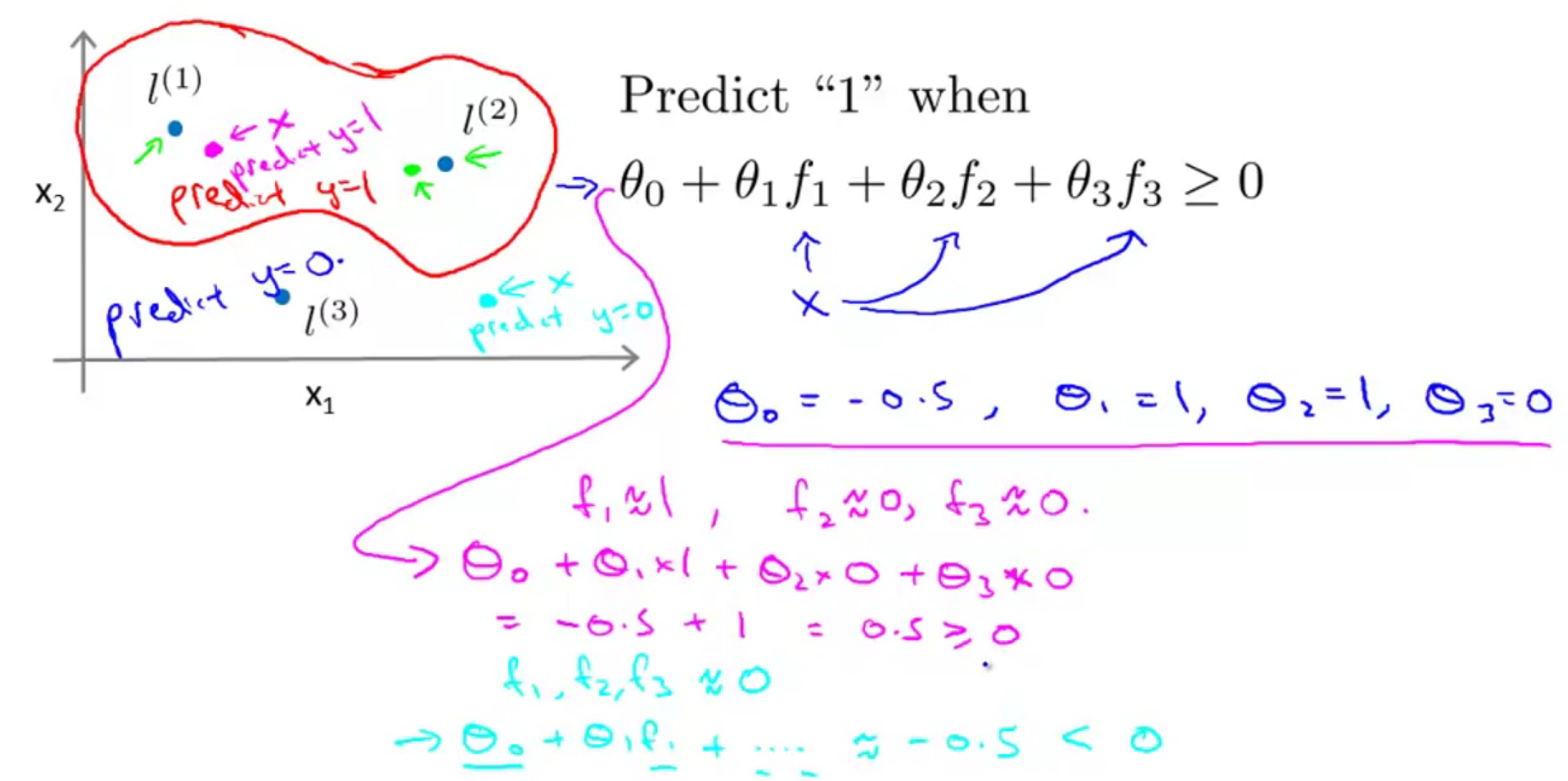
3.2 标记点的选取

前面介绍了为何核函数可以使SVM有非线性表达能力，那么我们应该如何选择标记点呢？我们通常是根据训练集的数量选择地标的数量，即如果训练集中有 m 个实例，则我们选取 m 个标记点，并且令：$l^{(1)}=x^{(1)},l^{(2)}=x^{(2)}, \ldots,l^{(m)}=x^{(m)}$ 。这样做的好处在于：现在我们得到的新特征是建立在原有特征与训练集中所有其他特征之间距离的基础之上的，即：

下面将核函数运用到支持向量机中，修改我们的支持向量机假设函数为：

在具体实现代码的过程中，我们还需要对最后的归一化项进行些微调整，在计算 $\sum_{j=1}^{n=m} \theta_{j}^{2}=\theta^{T} \theta$ 时，我们 用 $\theta^{\top} \mathrm{M} \theta$ 代替 $\theta^{\top} \theta$，其中 $M$ 是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算。但不了解也没事，因为有封装好的软件包可以使用。等）。在使用这些软件包最小化我们的代价函数之前，我们通常需要编写核函数，并且如果我们使用高斯核函数，那么在使用之前进行特征缩放是非常必要的。另外，支持向量机也可以不使用核函数 ，当我们不采用非常复杂的函数，或者我们的训练集特征非常多而实例非常少的时候，可以采用这种不带核函数的支持向量机。

3.3 参数对模型的影响

• C是惩罚系数，即对样本分错的宽容度，因为C后面跟的是代价函数，当样本分类错误时代价函数的值就会变大。C越高，则代价函数的变大效果就会被放大，说明越不能容忍出现分错,容易过拟合。C越小，容易欠拟合。C过大或过小，泛化能力变差。
• 如果 $\sigma$ 设的太小，容易导致过拟合。因为 $\sigma$ 很小的高斯分布长得又高又瘦，会造成只会作用于支持向量样本附近，对于未知样本分类效果很差，但训练准确率可以很高，(如果让无穷小，则理论上，高斯核的SVM可以拟合任何非线性数据，但容易过拟合)。

四、应用SVM

4.1 其他核函数

在高斯核函数之外我们还有其他一些选择，如：
多项式核函数（Polynomial Kernel）

字符串核函数（String kernel）

卡方核函数（chi square kernel）

直方图交集核函数（histogram intersection kernel）

这些核函数的目标也都是根据训练集和标记点之间的距离来构建新特征，这些核函数需要满足 Mercer's 定理，才能被支持向量机的优化软件正确处理。

4.2 多分类问题

4.2.1 一对多OVA

一对多算法 (one-against-rest/one-against-all)是最简单的实现方法,也是支持向量机多类分类的最早实现方法。构造一系列两类分类机，其中的每一个分类机都把其中的一类同余下各类分划开，然后据此判断某个输入x的归属。假设一共有 $k$ 类样本，将其中第 $j$ 类样本看作正类$(j=1,2,…,k)$，而将其它 $k-1$ 类样本看作负类，进行 $k$ 次判断，将概率最大的当做结果。

4.2.2 一对一 OVO

成对分类法(one-against-one)是基于两类问题的分类方法。它的思想是利用两类SVM算法分别在每两类不同的样本之间都构造一个最优决策面，如果一共k类样本，则需要构造 $\frac{k(k-1)}{2},(k>2)$ 个分类平面，这种方法相当于将多类问题转化为多个两类问题来求解，本质上跟两类SVM一样。接下往往采用投票法(Vote)，计算所有的分类器所分得的类别，选择得票数最多的类别作为预测结果。

4.3 SVM与逻辑回归

n 为 特征数， m 为 训练 样本数。

• 如果相较于 m 而言， n 要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。
• 如果 n 较小，而且 m 大小中等，例如 n 在 1-1000 之间，而 m 在 10-10000 之间，使用 高 斯核函数的支持向量机。
• 如果 n 较小，而 m 较大，例如 n 在 1-1000 之间，而 m 大于 50000 ，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。