CS231n第九节：循环神经网络RNN

原文传送门：Recurrent Neural Networks

本系列文章基于CS231n课程，记录自己的学习过程，所用视频资料为 2017年版CS231n，阅读材料为CS231n官网2022年春季课程相关材料

参考资料：

Herb的CS231n课程学习笔记

The Unreasonable Effectiveness of Recurrent Neural Networks

上篇文章的翻译：循环神经网络惊人的有效性

1. RNN介绍

1.2 模型分类

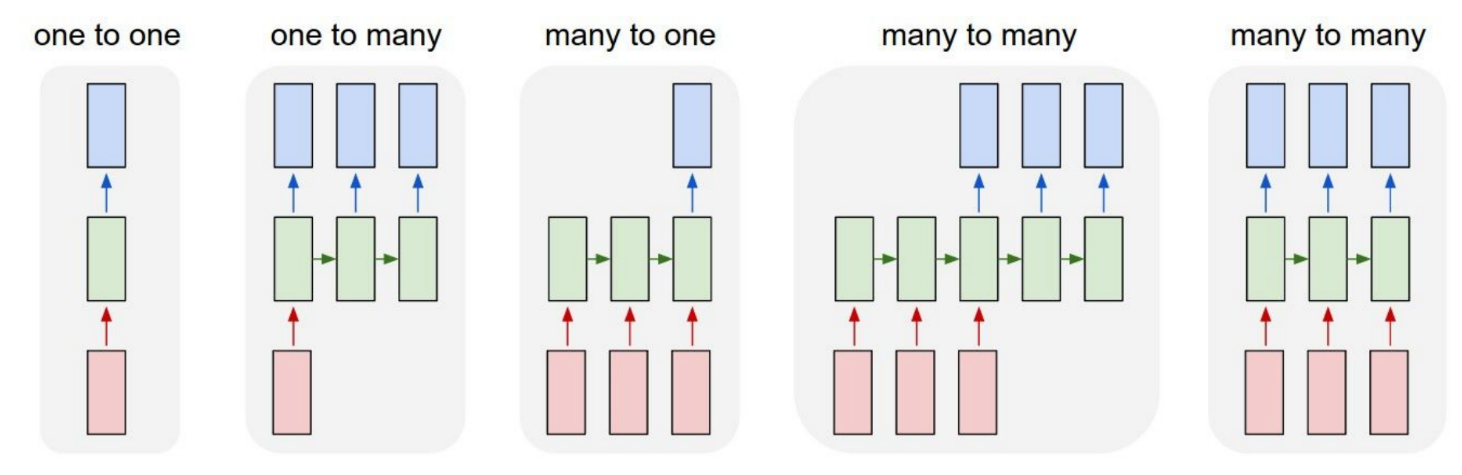
本章我们将介绍 循环神经网络 Recurrent Neural Networks （RNNs），RNN的一大优点是为网络结构的搭建提供了很大的灵活性。通常情况下，我们提及的神经网络一般有一个固定的输入，然后经过一些隐藏层的处理，得到一个固定大小的输出向量（如下图左所示，其中红色表示输入，绿色表示隐藏层，蓝色表示输出，下同）。这种“原始”的神经网络接受一个输入，并产生一个输出，但是有些任务需要产生多个输出，即一对多的模型（如下图 one-to-many标签所示）。循环神经网络使得我们可以输入一个序列，或者输出一个序列，或者同时输入和输出一个序列。下面按照输入输出是否为一个序列对RNN进行划分，并给出每种模型的一个应用场景：

• 一对一模型 one-to-one，最原始的模型，略过。
• 一对多模型 one-to-many，比如说给图片添加字幕，即给出一张固定大小的图片，然后生成一个单词序列描述图片的内容。
• 多对一模型 many-to-one，比如说动作预测任务。输入一串视频帧的序列，然后生成一个标签代表这个视频中发生了什么动作。另外一个多对一任务的例子是NLP领域的情感分类任务，给出一个句子的单词串，然后判断这个句子的情感类别。
• 多对多模型 many-tomany，比如说给视频添加字幕，输入的是一串视频帧的序列，生成的是描述视频内容的字幕。另外一个例子是NLP领域的机器翻译任务，比如说将一串英文单词组成的序列翻译成法语单词组成的序列。
• 此外，还有一种多对多模型的变种，这种变种模型会在每个时间节点都生成一个输出，一个例子是视频帧级别的视频分类任务，即对视频的每一帧都进行分类，并且模型预测的标准并不只依靠当前帧的内容，而是在这个视频中此帧之前的所有内容。

相较于那些从一开始连计算步骤的都定下的固定网络，序列体制的操作要强大得多。并且对于那些和我们一样希望构建一个更加智能的系统的人来说，这样的网络也更有吸引力。我们后面还会看到，RNN将其输入向量、状态向量和一个固定（可学习的）函数结合起来生成一个新的状态向量。在程序的语境中，这可以理解为运行一个具有某些输入和内部变量的固定程序。从这个角度看，RNN本质上就是在描述程序。实际上RNN是具备图灵完备性的，只要有合适的权重，它们可以模拟任意的程序。然而就像神经网络的通用近似理论一样，你不用过于关注其中细节。实际上，我建议你忘了我刚才说过的话。

If training vanilla neural nets is optimization over functions, training recurrent nets is optimization over programs.

如果训练普通神经网络是对函数做最优化，那么训练循环网络就是针对程序做最优化。

无序列也能进行序列化处理。你可能会想，将序列作为输入或输出的情况是相对少见的，但是需要认识到的重要一点是：即使输入或输出是固定尺寸的向量，依然可以使用这个强大的形式体系以序列化的方式对它们进行处理。例如，下图来自于DeepMind的两篇非常不错的论文。左侧动图显示的是一个算法学习到了一个循环网络的策略，该策略能够引导它对图像进行观察；更具体一些，就是它学会了如何从左往右地阅读建筑的门牌号（Ba et al）。右边动图显示的是一个循环网络通过序列化地学习，学会以序列的形式逐步向画布上添加颜色，生成了写有数字的图片，这些图片的样式和训练集中的图片类似（Gregor et al）。

必须理解到的一点就是：即使数据不是序列的形式，仍然可以构建并训练出能够进行序列化处理数据的强大模型。换句话说，你是要让模型学习到一个处理固定尺寸数据的分阶段程序。

1.2 卷积网络的不足

卷积神经网络不能很好地处理输入和输出是可变序列的任务。比如说给视频添加字幕，输入是一个可变的视频帧（比如说可能是10分钟的也可能是10小时的视频），而输出也是不定长度的字幕。而卷积神经网络只能接收固定长宽大小的输入，并且不能很好地泛化到不同大小的输入。为了解决这一问题，我们需要学习循环神经网络RNN。

1.3 RNN概念

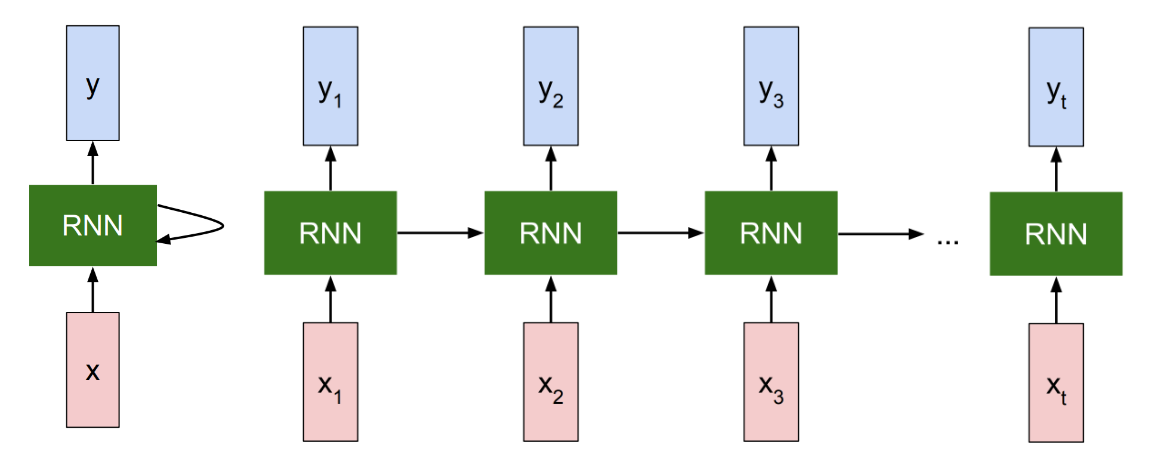
RNN基本上就是一个黑盒（如下图左所示），当逐一处理一个输入的序列时，黑盒中的“内部状态”也会随之更新。在每个时间段，我们向RNN输入一个向量，RNN将这个内部状态（上一时间段的状态）和输入的向量一起作为接收到的输入。当我们调整RNN的权重时，RNN在接受同样的输入后，会对内部状态产生不一样的改变。同时，我们也需要模型基于这个内部状态产生一个输出。因此，我们可以在RNN的顶端产生这些输出（如下图顶部所示）。

如果我们将RNN模型展开（如下图右所示），那么每一个时间段的输入对应的是输入序列的每个元素（比如视频序列的每一帧），记作 $x_1,x_2,...,x_t$ 。RNN在每个时间段会得到两个输入，一个来自输入序列的元素 $x_i$ ，另外一个就是对之前信息的一种表示形式（即对历史信息的记录，也就是上一段提到的内部信息）。然后，RNN会生成一个输出 $y_i$ ，同时更新这个历史信息，RNN会进行很多次这样的前向传播。下图右边所示的每个RNN块都是同一个RNN网络，他们拥有同样的参数，但是在每个时间段会接受不同的输入和历史信息。

更加精确地说，RNN可以表示成一个循环的公式，公式由一些包含参数 $W$ 的函数 $f_W$ 组成：

即，每个时间段它接收一些先前的状态 $h_{t-1}$，这里我们用向量 $h_{t-1}$ 表示第 $t-1$ 个时间段的信息。同时接收此时的输入 $x_t$，用两个输入共同生成当前状态 $h_t$ 。一个固定的函数 $f_W$ 被用于每一个时间段，这也允许我们使用在序列上使用RNN模型，并且不用预先给出输入序列的大小。因为，我们在每个单独的时间段都使用一个相同的函数，所以输入和输出的长度也就无关紧要了。

最简单的RNN形式，也称为原始RNN（Vanilla RNN）， 网络中只有一个单一的隐藏状态 $h$ ，在网络中我们使用一个循环的公式来更新隐藏状态 $h$ ，并作为一个函数接受先前的隐藏状态 $h_{t-1}$ 和当前时间段的输入 $x_t$ 。特别的，我们使用权重矩阵 $W_{hh}$ 和 $W_{xh}$ 对 $h_{t-1}$ 和 $x_t$ 进行投影，同时将结果相加后使用 $tanh$ 进行放缩。也就是说，这样一个循环的公式表示，在 $t$ 时刻，状态 $h$ 是由一个包含 $h_{t-1}$ 和 $x_t$ 作为输入的函数进行更新的，公式如下：

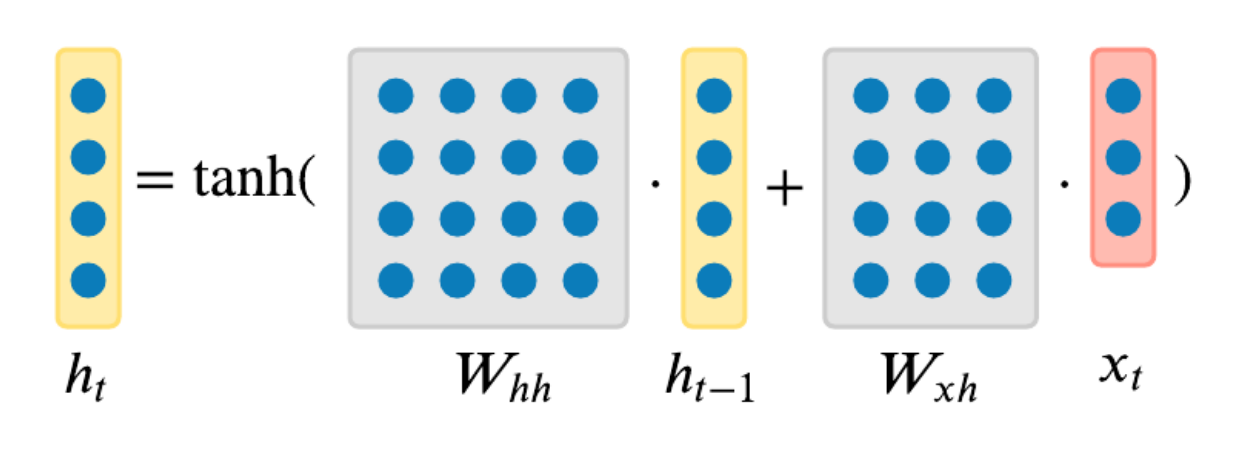
我们可以依据状态 $h_t$ 来进行预测，这是构建一个神经网络最简单的形式：

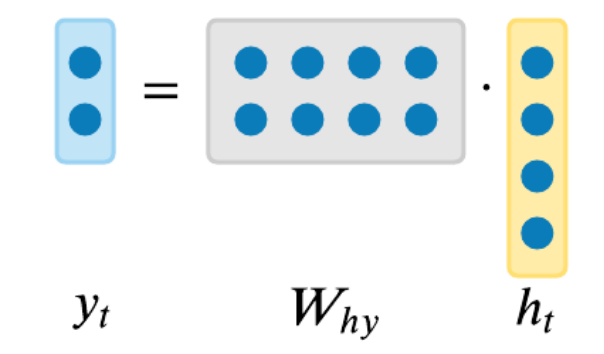
也就是说，RNN可以抽象成一个简单的API：它接受输入，然后返回输出，不过输出不仅受输入影响，还会受到历史输入的影响，这个历史输入以隐藏状态 $h$ 的形式存储。并且，如果将RNN抽象成一个类，那么每次输出都只经历一个 step：

class RNN:
  # ...
  def step(self, x):
    # 更新隐藏状态h
    self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))
    # 计算输出向量y
    y = np.dot(self.W_hy, self.h)
    return y

rnn = RNN()
y = rnn.step(x) # x是输入向量，y是输出向量

2. RNN作为字符级的语言模型

使用RNN的最简单的方式之一是字符级语言模型，因为它是很直观的。在这种方式中，RNN的工作方式是接收一串字母，在每一个时间段，我们都会要求RNN去预测序列中可能出现的下一个字母是什么。RNN的预测结果会以一个得分分布的形式给出，代表了RNN认为在字母表中的每个字母在接下来出现的可能性。

所以假设有一个非常简单的例子（如下图所示），我们有字母表 v ∈ {"h","e","l","o"}，然后利用训练序列“hello”训练RNN。该训练序列实际上是由4个训练样本组成：1.当h为上文时，下文字母选择的概率应该是e最高。2.l应该是he的下文。3.l应该是hel文本的下文。4.o应该是hell文本的下文。

具体来说，我们会用独热编码的方法给每个字母编码，然后利用step方法一次一个地将其输入给RNN。随后将观察到4维向量的序列（一个字母一个维度）。我们将这些输出向量理解为RNN关于序列下一个字母预测的信心程度。下面是流程图：

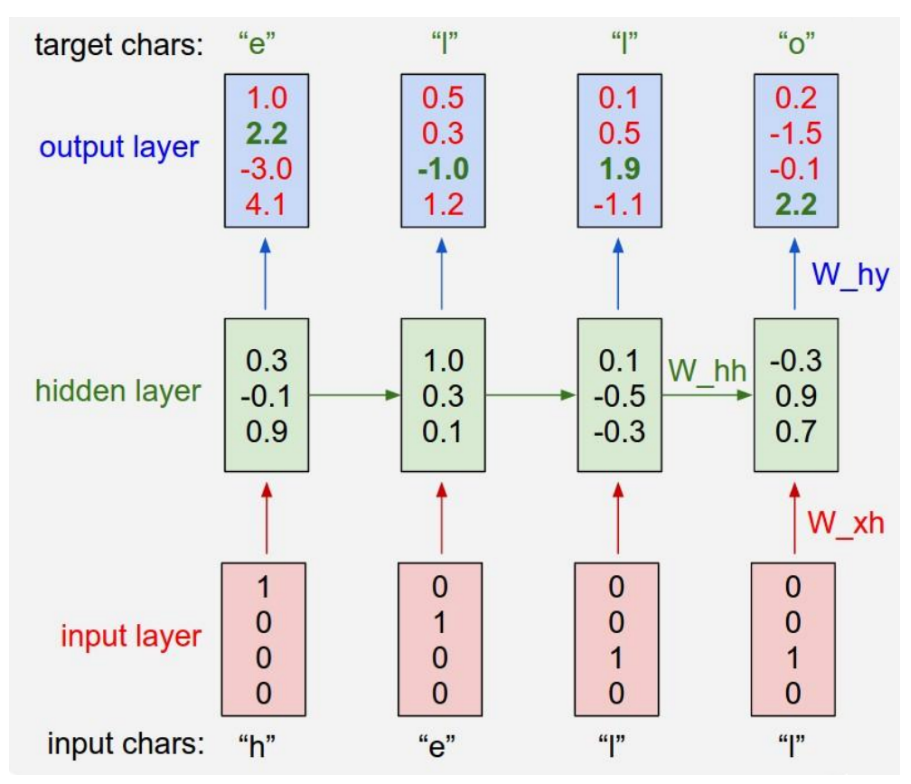
具体来说，我们每次向RNN中输入一个字母，首先是 "h" ，然后是 "e"，然后 "l"，最后是 "l"。每个字母使用独热编码（one-hot）来表示 ，如下图所示：

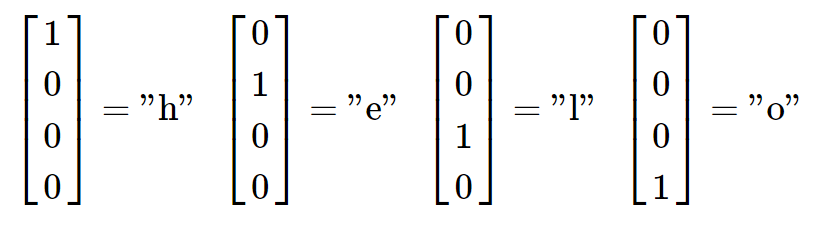
然后，我们在每一时间段中使用上文提到的迭代的公式，并假设我们初始的状态 $h$ 是一个全0的3维向量。通过这一个不变的迭代公式，最终我们也会得到一个三维的向量表示下一个隐藏状态 $h$ ，如下图所示：

当我们在每一时间段都使用这样一个迭代，我们就可以在每一时间段都预测下一个可能出现的字母。由于在字母表中有4个字母，所以我们预测的结果也是一个4维的向量。在最开始，我们输入字母 "h" ，RNN依据当时的权值计算出一个向量，表示每个字母出现的可能性：

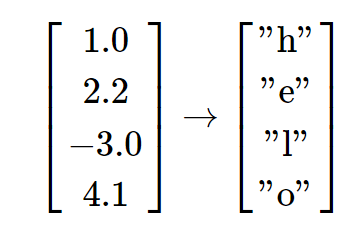
即，RNN认为下一个字母时 "h" 的可能性为 1.0 ，认为是 "e" 的可能性为 2.2 ，认为是 "l" 的可能性为 -3.0 ，认为是 "o" 的可能性为 4.1，因此RNN预测下一个字母应该是 "o"，当然我们知道 "h" 的下一个字母应该是 "e" ，所以实际上，2.2才是正确答案对应的得分。所以我们希望正确答案对应的得分尽可能的高，而其他的得分尽可能的低。类似的，在每一步都有一个目标字母，我们希望算法分配给该字母的置信度应该更大。因为RNN包含的整个操作都是可微分的，所以我们可以通过对算法进行反向传播（微积分中链式法则的递归使用）来求得权重调整的正确方向，在正确方向上可以提升正确目标字母的得分。然后进行参数更新，即在该方向上轻微移动权重。如果我们将同样的数据输入给RNN，在参数更新后将会发现正确字母的得分（比如第一步中的e）将会变高（例如从2.2变成2.3），不正确字母的得分将会降低。重复进行一个过程很多次直到网络收敛，其预测与训练数据连贯一致，总是能正确预测下一个字母。

更技术一点的解释是，我们选用比如softmax分类器（交叉熵损失）等一类的损失函数，使用小批量的随机梯度下降来训练RNN，将损失值从最后一个时刻往前反向传播回去，以此来计算在参数矩阵上的梯度，并使用RMSProp或Adam来让参数稳定更新，使得我们可以改变矩阵让RNN预测的正确答案的概率最大。

注意当字母l第一次输入时，目标字母是l，但第二次的目标是o。因此RNN不能只靠当前的输入数据，必须使用它的循环连接来保持对上下文的跟踪，以此来完成任务。在测试时，我们向RNN输入一个字母，得到其预测下一个字母的得分分布。我们根据这个分布取出得分最大的字母，然后将其输入给RNN以得到下一个字母。重复这个过程，我们就得到了文本！这是网上的一个RNN的简单实现代码：RNN Implementation using NumPy

3. 多层RNN

目前为止，我们只展现了一层的RNN，实际上我们并没有被限制只能使用单层的架构。今天，RNN的使用方式之一是以更复杂的方式。RNN可以被堆叠在一起组成多层的结构，以此达到更深的深度，而根据经验，更深的架构往往效果更好。如下图，就是使用了三个不同的RNN，每个RNN使用一组独立的权重。三个RNN依次堆叠在另一个的上面，所以，第二个RNN的输入就是第一个RNN的隐藏状态，所有堆叠的RNN被这样联合在一起训练。

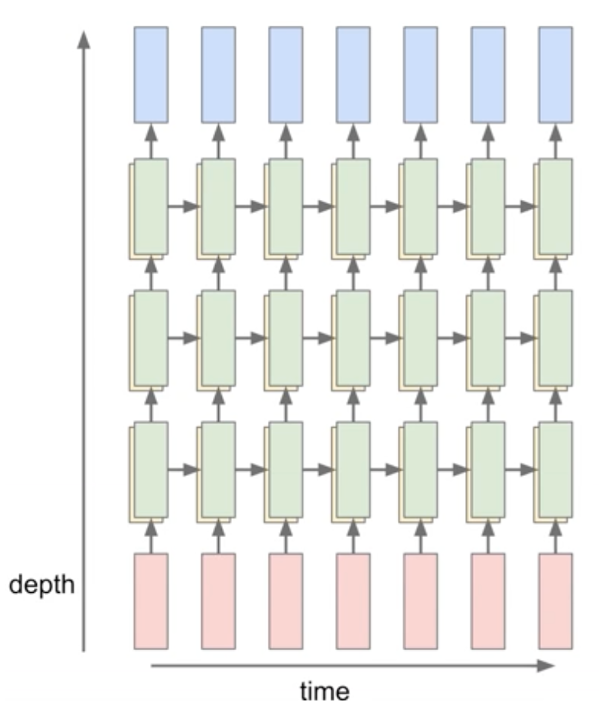
同样，我们可以把这个更深的网络抽象成上文提到的RNN类，那么每次输出就变成了（以两层网络为例）：

y1 = rnn1.step(x)
y = rnn2.step(y1)

换句话说，我们分别有两个RNN：一个RNN接受输入向量，第二个RNN以第一个RNN的输出作为其输入。其实就RNN本身来说，它们并不在乎谁是谁的输入：都是向量的进进出出，都是在反向传播时梯度通过每个模型。

 

4. 长短期记忆LSTM

到此为止，我们已经介绍了一个用于原始RNN的简单递推公式。实际运用中，我们实际上很少使用这种原始RNN的公式，作为替换，我们会使用长短期记忆RNN，即 Long-Short Term Memory (LSTM) RNN。

4.1 原始RNN的梯度溢出和梯度消失

一个RNN区块接收输入 $x_t$ 以及先前的隐藏信息 $h_{t-1}$ 并学习如何翻译，通过 tanh 来生成当前的隐藏信息 $h_t$ 和输出 $y_t$ ，公式如下：

对于反向传播，我们来检查最后一个时间段的输出如何影响最早时间段时的权重， $h_t$ 对于 $h_{t-1}$ 的偏导数可以写作： $\frac{\partial h_{t}}{\partial h_{t-1}}=\tanh ^{\prime}\left(W_{h h} h_{t-1}+W_{x h} x_{t}\right) W_{h h}$，然后我们获取 $t$ 时刻的损失值对于权重 $W_{hh}$ 的偏导数：

• 梯度消失： 我们可以从 $\tanh ^{\prime}\left(W_{h h} h_{t-1}+W_{x h} x_{t}\right)$ 中看出，这一项的值始终小于1，因为 tanh的倒数值域小于1。因此，随着 $t$ 的变大（即经过更多的时间段），梯度值也会随之变小直至接近0。这就导致了梯度消失（梯度弥散）问题，即处于后面时间段的梯度几乎对前面时间段的梯度无法造成影响（反向传播会将本地梯度和上游梯度相乘），当我们对长序列的输入进行建模时，这是有问题的，因为更新会非常慢。

• 移除非线性（tanh)：上面的梯度消失问题貌似是由于tanh导致的，那么如果我们将tanh移除，是否就能解决这个问题呢？首先原先计算的梯度公式会变成：$\frac{\partial L_{t}}{\partial W}=\frac{\partial L_{t}}{\partial h_{t}}\left(\prod_{t=2}^{T} W_{h h}^{T-1}\right) \frac{\partial h_{1}}{\partial W}$，这就会引来一下问题：

  • 梯度爆炸：如果有一个 $W_{hh}$ 的值是大于1的，那么梯度就会越来越大，直到出现NaNs错误。
  • 梯度消失：是的，移除非线性无法避免梯度消失。当所有的 $W_{hh}$ 值小于1，那么梯度就会越来越小，越来越接近0。

实践中，我们可以通过梯度裁剪的方式避免梯度爆炸问题，即限制大的梯度小于一个最大的门限值。但是梯度消失的问题仍然无法解决，所以LSTM就被设计出来用以解决这个问题。

4.2 LSTM表达式

接下来是对LSTM的精确表示。在第 $t$ 步时，此时有隐藏状态 $h_t$ ，细胞状态（cell state） $c_t$ ，这两者都是大小为 $n$ 的向量。一个LSTM和RNN的区别是，它含有一个额外的细胞状态 $c_t$ ,直觉上来说，$c_t$ 可以看成存储了长期的信息。LSTM可以读取、擦除、写入信息到细胞状态 $c_t$ 中。LSTM修改 $c_t$ 的方法是通过三个特殊的门（gate）：$i,f,o$ ，分别对应着输入门、遗忘门、输出门。这三个门的取值在0到1之间，其中0表示关闭，1表示开启。三个门都是 $n$ 维的向量。

在每一个时间段，我们都拥有一个输入向量 $x_t$ ，一个先前的隐藏状态 $h_{t-1}$ ，一个先前的细胞状态 $c_{t-1}$ ，LSTM通过下述式子计算下一个隐藏状态 $h_t$ ，下一个细胞状态 $c_t$：

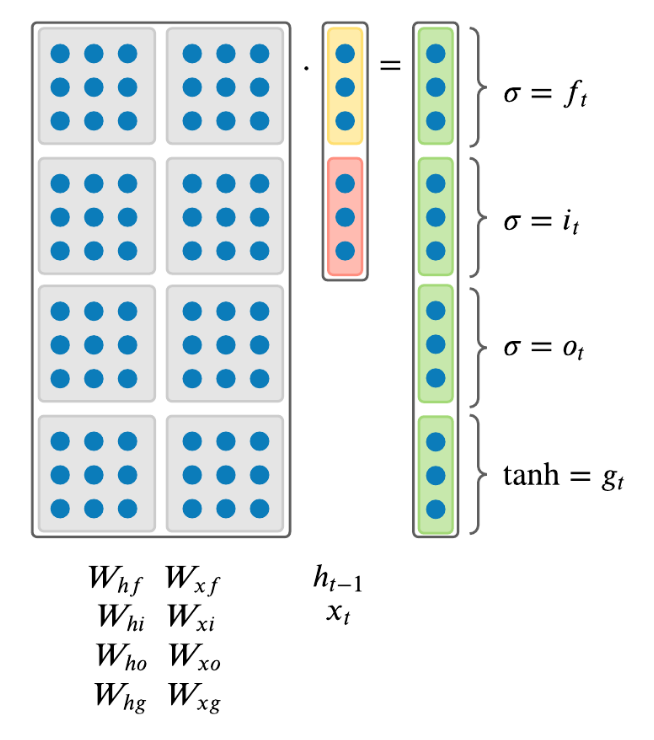
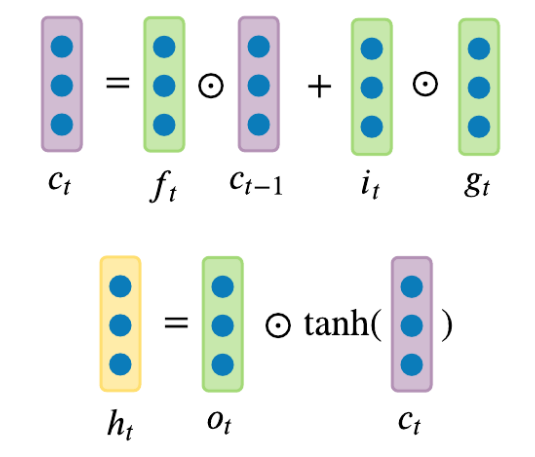
其中 $\odot$ 表示哈达玛积 Hadamard Product，$g_t$ 是一个中间变量用于暂存计算结果。

哈达玛积举例：

$f,i,o$ 的值都是在0到1之间，因为它们都被使用sigmoid函数 $\sigma$ 进行放缩，当进行逐元素的乘法运算时，我们可以了解到：

• 遗忘门$f_t$： 控制有多少来自 $c_{t-1}$ 的信息该被移除。遗忘门用于学习删除来自早先时间节点的隐藏信息，这也是为什么LSTM有两个隐藏信息 $h_t$ 和 $c_t$ ，因为 $c_t$ 将会被一直传播下去，并且学习是否忘记部分来自先前细胞的状态。
• 输入门$i_t$： 控制有多少来自 $h_{t-1}$ 和 $x_t$ 的信息应该被添加到 $c_t$ 中。 输入门使用的是sigmoid函数，可以将输入的值缩放到0到1之间。如果其值要么几乎总是0，或者要么总是1时，输入门就可以看成一个开关。它决定了是否将RNN的输出结果$g_t$ 添加到 $c_t$ 中。
• 输出门$o_t$： 控制有多少来自 $h_t$ 的信息需要被作为输出值展示。

LSTM的关键思想是细胞状态（cell state），即贯穿于循环时间段之间的水平线。你可以把细胞状态想象成某种信息的高速公路，沿着整个链条在时间上笔直地流过，期间只有一些微小的线性互动。有了上面的公式表达，信息很容易就沿着这条高速公路流动（如下图加粗的横线）。因此，即使有一堆LSTM堆积在一起，我们也可以得到一个不间断的梯度流，梯度通过细胞状态而不是隐藏状态 $h$ 回流，因此在时间段中梯度不会消失。

这极大地解决了我们上面概述的梯度消失/爆炸的问题。下图还显示，梯度包含一个 "遗忘 "门的激活矢量。这允许通过使用 "遗忘 "门的适当参数更新来更好地控制梯度值。

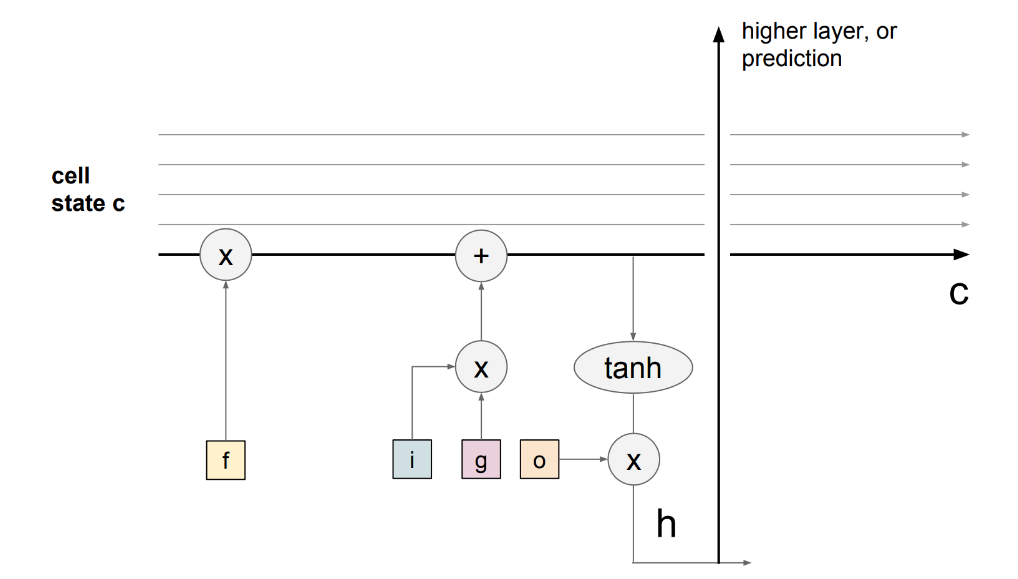
4.3 LSTM是否解决了梯度消失问题

LSTM结构使RNN更容易在许多循环时间段中保存信息。例如，如果遗忘门被设置为1，而输入门被设置为0，那么细胞状态的信息将在许多循环时间步骤中始终被保留。相比之下，对于原始的RNN来说，仅仅利用单一的权重矩阵，就很难在循环时间步骤中保留隐藏状态的信息。不过LSTM不能保证没有消失/爆炸的梯度问题，但它确实为模型学习序列中长距离的依赖关系提供了一种更容易的方法。

5. 理解训练的过程

本节原文来自 The Unreasonable Effectiveness of Recurrent Neural Networks

参考译文：循环神经网络惊人的有效性

5.1 训练时输出文本的进化

RNN或者说LSTM到底是如何运作的呢？现在跑两个小实验来一探究竟。首先，观察模型在训练时输出文本的不断进化是很有意思的。例如，我使用托尔斯泰的《战争与和平》来训练LSTM，并在训练过程中每迭代100次就输出一段文本。在第100次迭代时，模型输出的文本是随机排列的，但是至少可以看到它学会了单词是被空格所分割的，只是有时候它使用了两个连续空格。它还没学到逗号后面总是有个空格：

tyntd-iafhatawiaoihrdemot  lytdws  e ,tfti, astai f ogoh eoase rrranbyne 'nhthnee e 
plia tklrgd t o idoe ns,smtt   h ne etie h,hregtrs nigtike,aoaenns lng

在迭代到第300次的时候，可以看到模型学会使用引号和句号。单词被空格所分割，模型开始知道在句子末尾使用句号：

"Tmont thithey" fomesscerliund
Keushey. Thom here
sheulke, anmerenith ol sivh I lalterthend Bleipile shuwy fil on aseterlome
coaniogennc Phe lism thond hon at. MeiDimorotion in ther thize."

在第500次迭代时，模型开始学会使用最短和最常用的单词，比如“we”、“He”、“His”、“Which”、“and”等。：

we counter. He stutn co des. His stanted out one ofler that concossions and was 
to gearang reay Jotrets and with fre colt otf paitt thin wall. Which das stimn 

从第700次迭代开始，可以看见更多和英语单词形似的文本：

Aftair fall unsuch that the hall for Prince Velzonski's that me of
her hearly, and behs to so arwage fiving were to it beloge, pavu say falling misfort 
how, and Gogition is so overelical and ofter.

在第1200次迭代，我们可以看见使用引号、问好和感叹号，更长的单词也出现了：

"Kite vouch!" he repeated by her
door. "But I would be done and quarts, feeling, then, son is people...."

在迭代到2000次的时候，模型开始正确的拼写单词，引用句子和人名：

"Why do what that day," replied Natasha, and wishing to himself the fact the
princess, Princess Mary was easier, fed in had oftened him.
Pierre aking his soul came to the packs and drove up his father-in-law women.

从上述结果中可见，模型首先发现的是一般的单词加空格结构，然后开始学习单词；从短单词开始，然后学习更长的单词。由多个单词组成的话题和主题词要到训练后期才会出现。

5.2 RNN中的预测与神经元激活可视化

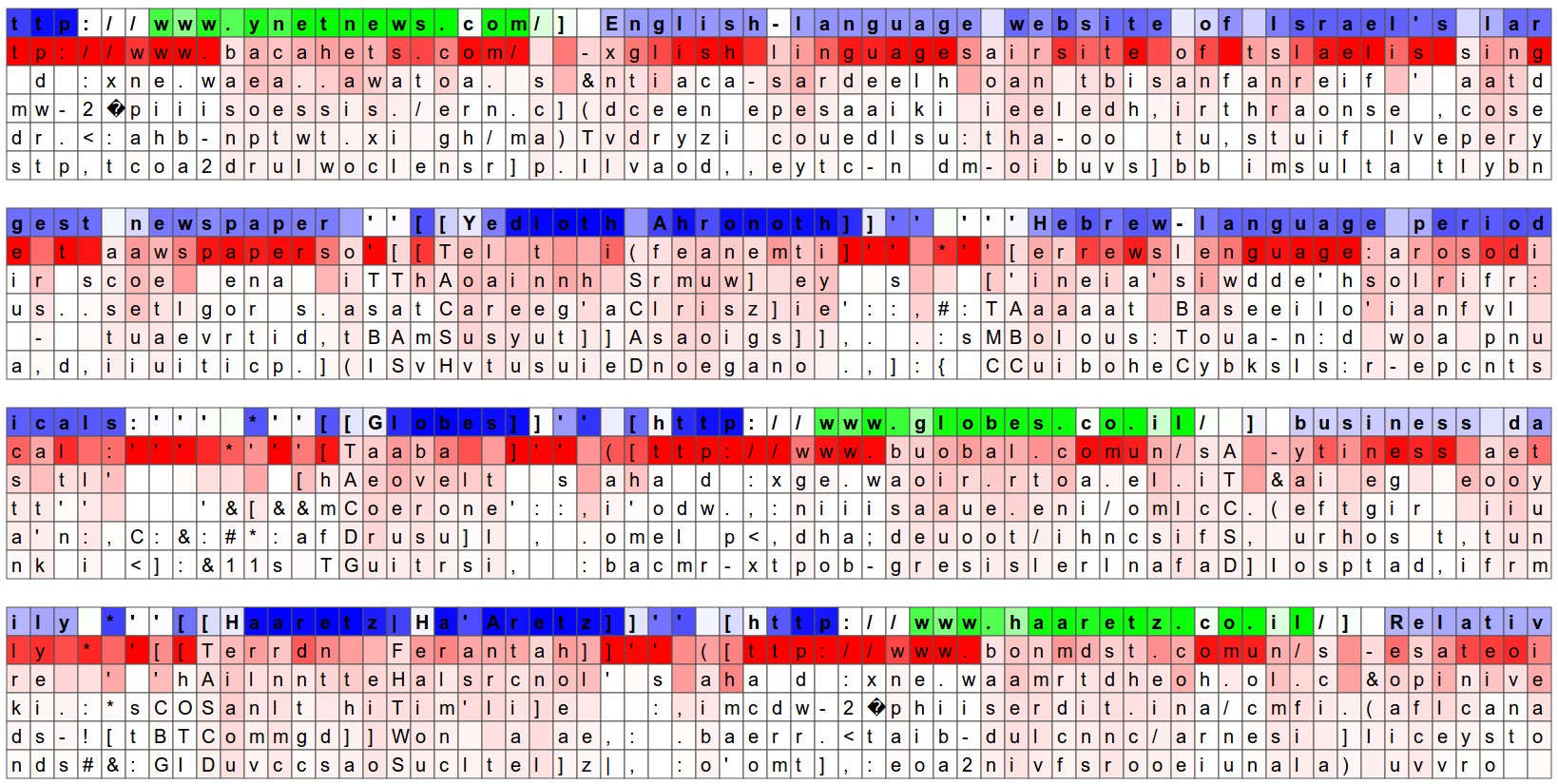
另一个有趣的实验内容就是将模型对于字符的预测可视化。下面的图示是我们对用维基百科内容训练的RNN模型输入验证集数据（蓝色和绿色的行）。在每个字母下面我们列举了模型预测的概率最高的5个字母，并用深浅不同的红色着色。深红代表模型认为概率很高，白色代表模型认为概率较低。注意有时候模型对于预测的字母是非常有信心的。比如在 http://www 序列中就是。

输入字母序列也被着以蓝色或者绿色，这代表的是RNN隐层表达中的某个随机挑选的神经元是否被激活。绿色代表非常兴奋，蓝色代表不怎么兴奋。LSTM中细节也与此类似，隐藏状态向量中的值是[-1, 1]，这就是经过各种操作并使用tanh计算后的LSTM细胞状态。直观地说，这就是当RNN阅读输入序列时，它的“大脑”中的某些神经元的激活率。不同的神经元关注的是不同的模式。在下面我们会看到4种不同的神经元，我认为比较有趣和能够直观理解（当然也有很多不能直观理解）。下图中，高亮的神经元（绿色）看起来对于URL的开始与结束非常敏感。LSTM看起来是用这个神经元来记忆自己是不是在一个URL中。

下图中，高亮的神经元看起来对于markdown符号 [[]] 的开始与结束非常敏感。有趣的是，一个 [ 符号不足以激活神经元，必须等到两个 [[ 同时出现。而判断有几个 [ 的任务看起来是由另一个神经元完成的。

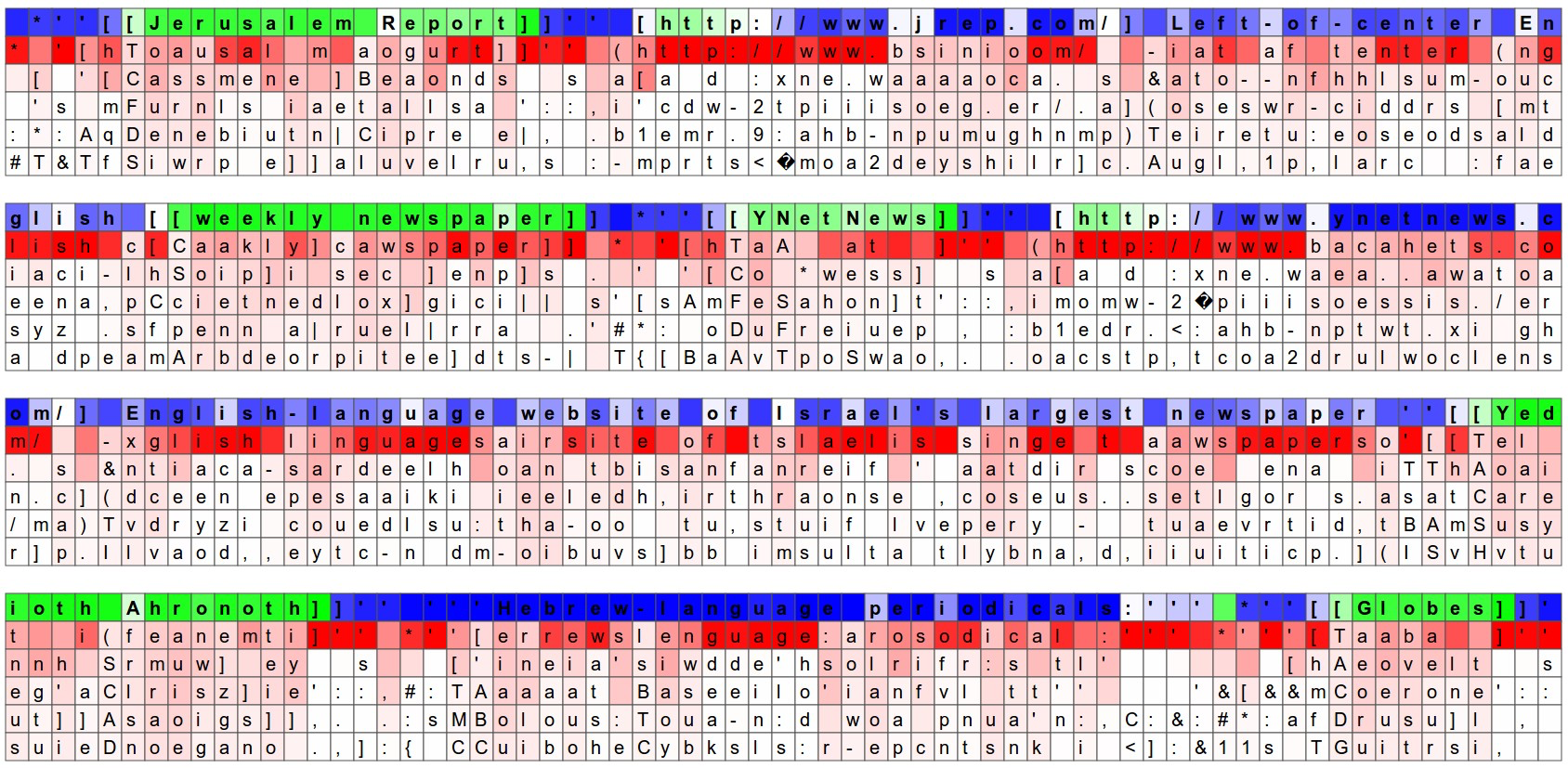
下图中显示的是一个在 [[]] 中线性变化的神经元。换句话说，在 [[]] 中，它的激活是为RNN提供了一个以时间为准的坐标系。RNN可以使用该信息来根据字符在 [[]] 中出现的先后来决定其出现的频率（也许？）。

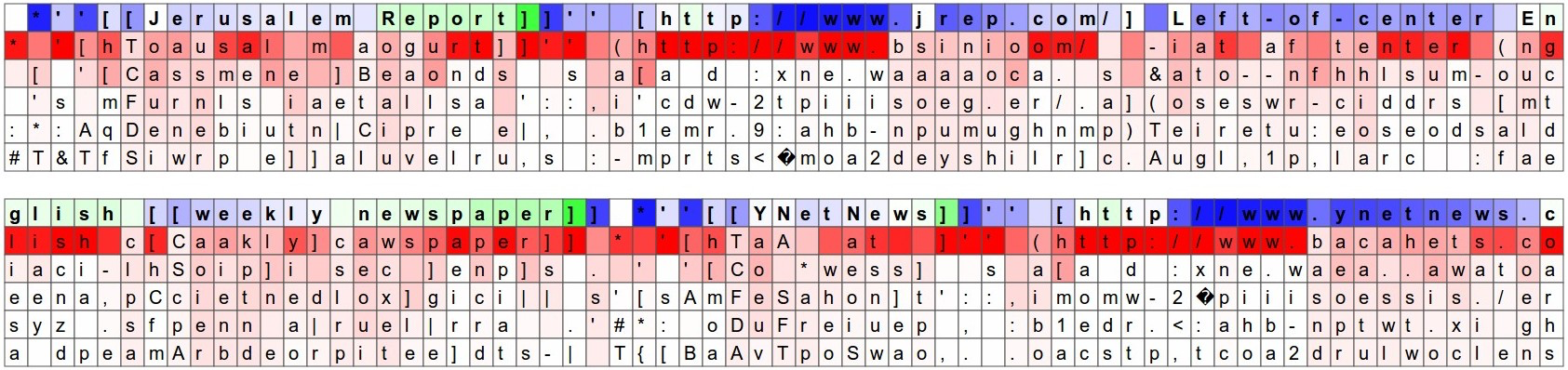
下图中显示的是一个进行局部动作的神经元：它大部分时候都很安静，直到出现www序列中的第一个w后，就突然关闭了。RNN可能是使用这个神经元来计算www序列有多长，这样它就知道是该输出有一个w呢，还是开始输出URL了。

当然，由于RNN的隐藏状态是一个巨大且分散的高维度表达，所以上面这些结论多少有一点手动调整。上面的这些可视化图片是用定制的HTML/CSS/Javascript实现的，如果你想实现类似的，可以查看这里。

我们可以进一步简化可视化效果：不显示预测字符仅仅显示文本，文本的着色代表神经元的激活情况。可以看到大部分的细胞做的事情不是那么直观能理解，但是其中5%看起来是学到了一些有趣并且能理解的算法：

 

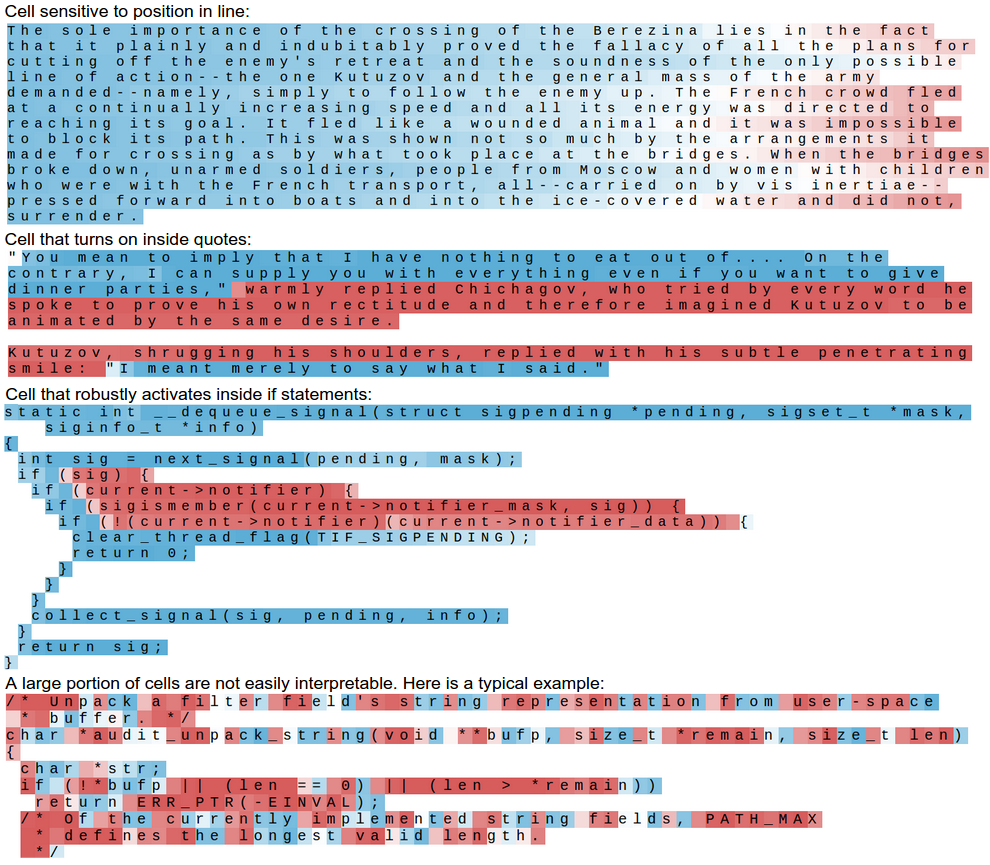
在预测下个字符的过程中优雅的一点是：我们不用进行任何的硬编码。比如，不用去实现判断我们到底是不是在一个引号之中。我们只是使用原始数据训练LSTM，然后它自己决定这是个有用的东西于是开始跟踪。换句话说，其中一个单元自己在训练中变成了引号探测单元，只因为这样有助于完成最终任务。这也是深度学习模型（更一般化地说是端到端训练）强大能力的一个简洁有力的证据。