树状数组

1.背景

讨论树状数组前我们先来思考一个问题，有一个长度为 $n$ 的数组，有两种操作：修改某个数的值和输出下标为 $i$ 到 $j$ 的每个数的和。

暴力做法：单点修改： $O(1)$ ，区间查询：$O(n)$
前缀和思想：单点修改： $O(n)$ ，区间查询：$O(1)$

对于这个问题的两个操作似乎是鱼和熊掌不可兼得一般——想要修改快，查询就慢；想要查询快，修改就慢。这时候你可能就会说了，线段树不就好了，但是线段树太繁琐了，我们有一个更好的工具：树状数组，它使得修改和查询都是 $O(logn) $级别，可谓是中庸思想的典范。

2. 思想

先介绍一个函数 lowbit(x)，其用途是找出 $x$ 的二进制表示中最低位的1的十进制，表示如 :

lowbit(12) = 4 // 12 = 1100, 最低位的1为100，十进制为4
lowbit(10) = 2  // 10的二进制为1010，最低位的1为 10 ,十进制为2
lowbit(9) = 1  // 9的二进制为1001，最低位的1为 1， 十进制为1

lowbit函数的实现也及其简单，int lowbit(x) {return x & -x;} ，具体原理涉及到计算机组成原理的部分知识（计算机负数的表示以及补码相关知识），不做详细介绍，记住就行。

树状数组主要运用到了位运算、倍增、前缀和的思想，就是将数组的前缀和拆分成几段，使得修改某个数的时间变快了，以长度为16的数组a[] 为例：

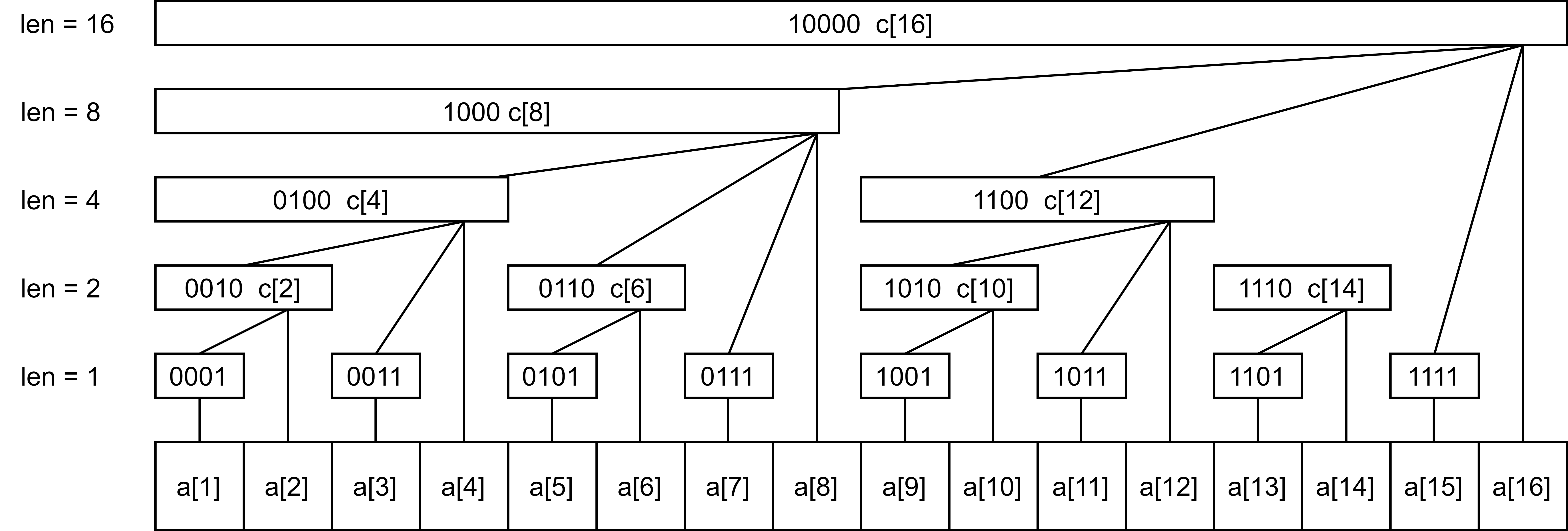
建立一个数组 c 来存储，c[x] 保持序列 a 的区间 [x - lobit(x) + 1, x] 中所有数字的和，如：

c[4] = a[1] + a[2] + a[3] + a[4] 
c[12] = a[9] + a[10] + a[11] + a[12] // lowbit(12) = 4

数组c就是上图中所有的长方形，可以看成一个树形结构：

最下面一行的数组a，代表叶子节点，存储每个数的值。
每个非叶子节点用数组c表示，c[x] 存储以它为根的所有子树中所有叶节点的和。
除树根外，每个非叶节点c[x] 的父节点为 c[x + lowbit(x)]
每个节点c[x] 的子节点的个数等于 lowbit(x)，如c[4] 有3个子节点，因为 lowbit(0100) = 100（二进制表示），有三位。

其实不用太过于纠结细节内容，只需要理解下面的代码实现就行了，树状数组属于思想巨难但是代码很简单的东西。

由于树的层数最多是 $logn$ 层这种方法查询和修改的时间复杂度都是 $O(nlogn)$ 的。

3. 实现

查询前缀和

int ask(int x) {
    int sum = 0;
    for(; x; x -= lowbit(x)) sum += c[x];
    return sum;
}

上述代码表示求 a[1] 到 a[x] 的所有值，比如求a[1] 到 a[7] 的值，其实就是求c[7] + c[6] + c[4] ，写成二进制的形式：c[0111] + c[0110] + c[0100] ，可以看到就是每次减掉一个最末尾的1，而其实现方式就是 -lowbit(x)，这里结合上面的图更好理解。

单点修改

void add(int x, int val) {
    for(; x <= n; x += lowbit(x)) c[x] += val;
}

上述代码表示将a[x] 加上val，n表示a数组的长度，由于c数组维护的是前缀和，所以要修改所有包含a[x] 的节点，其实现方式其实就是不断找x的父节点直到找到树根或者超过树根（x > n）。例如a[5] + val，就是要将 c[5], c[6], c[8], c[16] 都加val，下标转换成二进制分别为：0101，0110, 1000， 10000，从左到右其实就是不断地 + lowbit(x)实现。

初始化

针对一个原始数组a构造一个树状数组，一般就是先建立一个全为0的数组c，然后对于每个位置x，执行 add(x,a[x])即可。

4. 拓展

4.1 区间修改+单点查询

树状数组只能进行单点修改+区间查询的操作，我们可以利用差分思想将区间修改+单点查询的操作转换成单点修改+区间查询。定义差分数组 b[i] = a[i] - a[i-1] //a[i]为原数组，那么 $a[i] = \displaystyle \sum _{j = 1} ^ i b[i]$ ，即 a[i] 其实就是数组b的1到 i 的前缀和，这样就把 a[i] 的单点查询变成了 b[i] 的区间查询。对于a数组的区间修改，如果要将a[L] 到 a[R] 的值都 +val ，那么只要进行 b[L] + val , b[R+1] - val即可，这样就把区间修改变成了单点修改。

4.2 区间修改+ 区间查询

还是利用差分的思想，区间修改的做法和上面一样，至于区间查询，其实只要解决如果计算a数组的前缀和就解决了区间查询的问题了。对于a数组的前x个数的和，我们可以列出公式： $\displaystyle \sum _{i = 1} ^ x a[i] = \displaystyle \sum _{i = 1} ^ x \displaystyle \sum _{j = 1} ^ i b[i] = \displaystyle \sum _{i = 1} ^ x (x-i+1) * b[i] = \displaystyle (x+1)\sum _{i = 1} ^ x b[i] – \displaystyle \sum _{i = 1} ^ x i * b[i]$，图示推导过程如下：

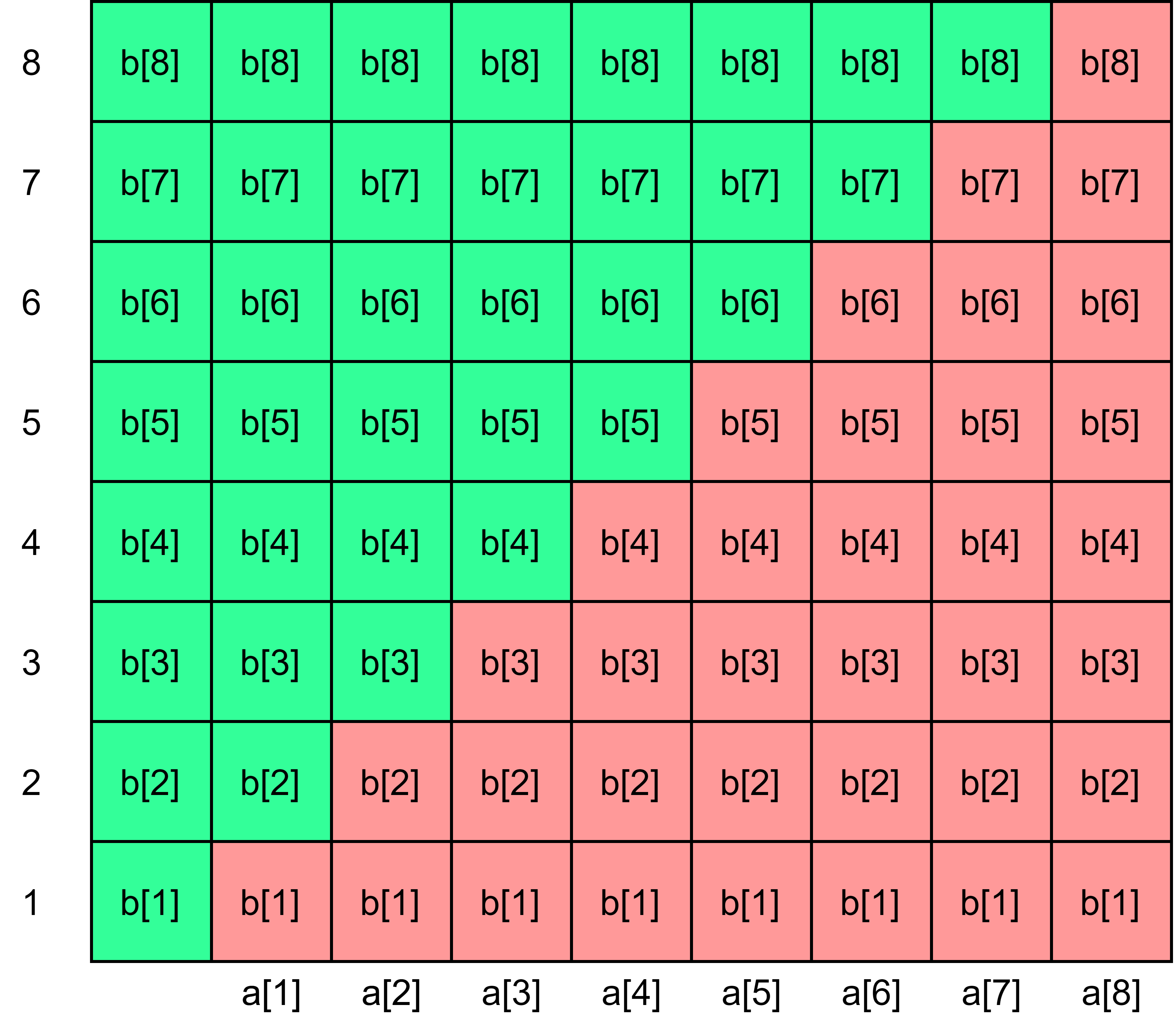
以x = 8为例，红色部分为所求的 a[1] 到 a[8] 的所有值，我们将其用绿色部分补充成一个正方形，整个正方形的值就是 $(x+1)\displaystyle \sum _{i = 1} ^ x b[i]$ ，绿色部分的值我们发现有一定的规律，就是$1 * b[1] + 2 * b[2] + 3 * b[3] + 4 * b[4] + … x * b[x]$ ，即：$\displaystyle \sum _{i = 1} ^ x i* b[i]$ ，两者相减就是红色部分，即： $\displaystyle (x+1)\sum _{i = 1} ^ x b[i] – \displaystyle \sum _{i = 1} ^ x i * b[i]$ 。所以我们只要对 b[i] 和 i * b[i] 进行树状数组的维护，就可以解决区间查询的问题了。