CS231n第十一节：生成模型

本系列文章基于CS231n课程，记录自己的学习过程，所用视频资料为 2017年版CS231n，阅读材料为CS231n官网2022年春季课程相关材料

本节将介绍一些无监督学习的内容，介绍一些生成模型，包括PixelRNN、PixelCNN、VAE、GAN

 

1. 无监督学习

和监督学习的最大区别就是数据中无标签，这带来的好处是可以轻松的获得大量的数据用于训练，比较常见的应用有：聚类、降维、特征学习、密度估计。

 

2. 生成模型

生成模型的定义就是给定一个训练数据，然后生成一些新的样本，保证和所给的训练集有一样的分布。即下图所示，假设训练集中满足分布 $p_{data}(x)$ ，我们要做的就是生成一些样本满足分布 $p_{model}(x)$ ，同时保证 $p_{model}(x) = p_{data}(x)$ 。

生成模型主要有以下这些应用场景：

• 生成逼真的艺术品图片，拥有超高的分辨率，着色等。
• 时间序列数据的生成模型可以用于仿真和规划（在强化学习中应用）。
• 训练生成模型还可以使隐式表征的推断成为有用的通用特征。

需要一提的是，可以将生成模型分成两大类，即隐式密度模型和显式密度模型，显式密度模型会显式地给出一个分布 $p_{model}(x)$ 使其和输入数据的分布相同。而隐式密度模型则不会给出一个分布，而是训练一个模型从输入数据中采样，并直接输出样本，而不用显式地给出分布的表达式。

目前常见（到2017年）的生成模型分类如下：

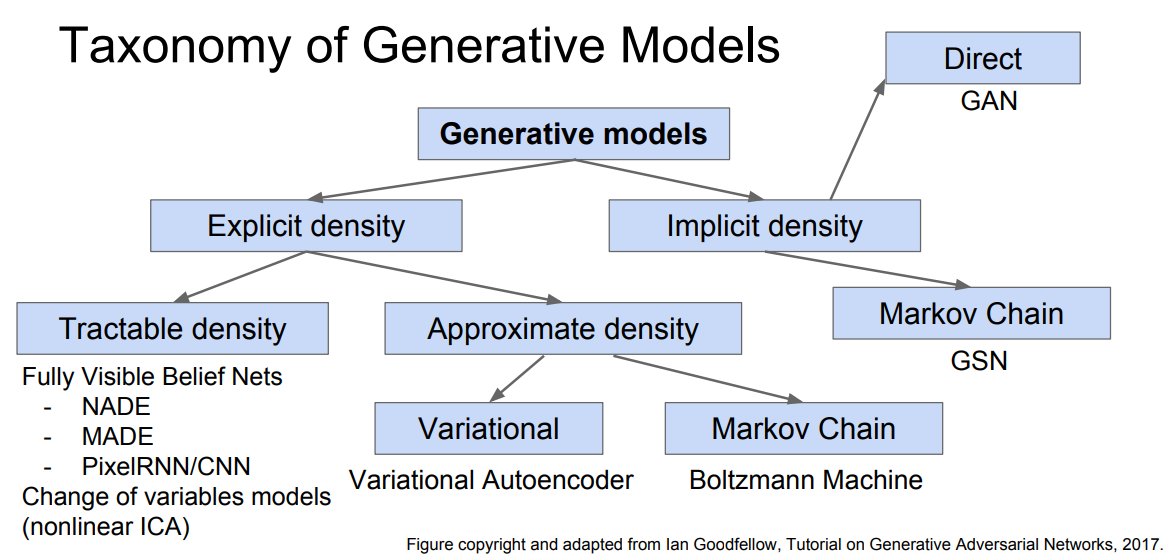
本文将介绍其中的PixelRNN、PixelCNN、VAE、GAN

2. PixelRNN 和 PixelCNN

2.1 定义

这两种网络除了属于显式密度模型，还属于全可见信念网络 （Fully visible belief network），他们以最大化下图所示的似然函数为目标来训练一个模型。

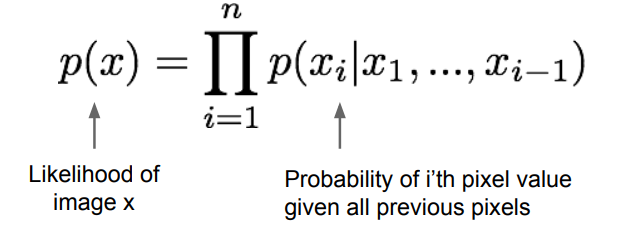
具体解释是：

首先解释这个式子的含义。对于生成一张图像，我们可以按照某个顺序逐一生成每个像素，假设第一个像素生成的概率为 $p(x_1)$，那么第二个像素生成的概率就定义成 $p(x_2|x_1)$ ，表示已经生成像素 $x_1$ 的条件下，生成第二个像素的概率，同理第三个像素的概率为 $p(x_3|x_1,x_2)$ ，于是第 $i$ 个像素生成概率为 $p(x_i|x_1,...,x_{i-1})$ ，因此整张图片的似然就可以表示成每个像素的条件概率的连乘形式。这里的似然代表的就是这个图片的概率密度，我们需要最大化似然函数，也就是使用极大似然估计法，其原理是认为已经存在的（输入的图片）必然出现的概率应该是最大的，所以我们就要使得其似然值最大。

似然和概率的理解不是很好，这里有点理不太清。

由于等式右边的每个像素的条件概率是很复杂的，所以我们可以使用神经网络来表达这些像素的概率分布。而上式提到的条件概率的定义是，给定所有下标小于 $i$ 的像素的条件下，那么我们首先就需要对像素进行排序，以此来明确像素的先后关系。

2.2 PixelRNN

在 PixelRNN 中，我们定义先后顺序如下：

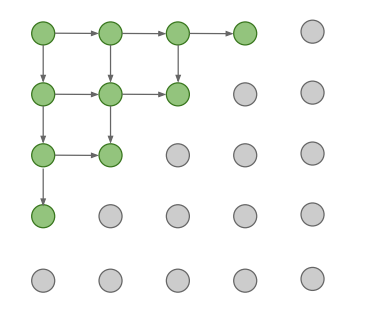
即，从输入图片的某个角落开始，如图中的左上角，然后逐步向右下角逐像素地拓展，由于RNN每个时间步的输出都依赖之前的输入，所以可以使用一个RNN来计算每个像素的条件概率值，一般使用LSTM来进行处理。接着，以最大化似然函数值来更新RNN参数即可。这样的效果不错，但是一个明显的缺点，就是按照顺序逐元素地计算并训练网络是十分慢的，同时在测试阶段，也是按照逐元素地生成像素，所以也会很慢。

2.3 PixelCNN

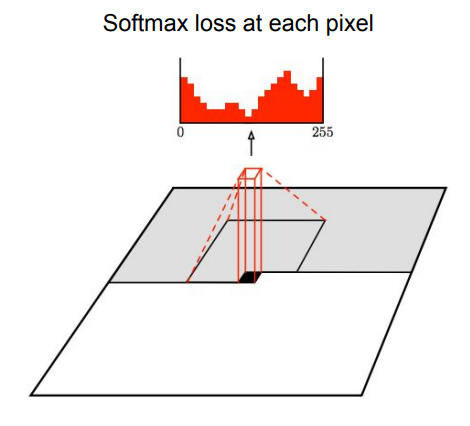
在 PixelCNN 中，我们也是从某个角落开始向外移动，但会使用CNN来处理元素之间的关系，如下图，灰色区域表示此时已经处理过的像素，当前正在处理黑色位置的像素。此时我们使用一个卷积核，其感受野如下图黑色框所示，这里可以看出，卷积核的感受野不是一个完整的正方形。这是因为，我们条件概率的定义是，以当前像素之前的像素为条件，所以，当前像素之后的像素信息是不能被获取的。这种特殊的卷积可以用一个掩码的方式来实现。由于 Pixel CNN 中计算时只使用到了图像中的像素信息，所以我们其实可以直接并行计算出所有像素的结果（使用矩阵乘法）。而不用RNN那样，受制于序列顺序关系（每次输出结果受上一次的输入影响），一次只能算一个像素。所以，在训练阶段，CNN会比RNN快，但是在测试阶段，CNN同样也是逐像素生成图片，速度依然很慢。

此外，在实现时，使用256个卷积核，在每个位置都会生成256个结果代表像素的0-255的取值，然后就可以当做是个分类问题，使用交叉熵损失函数来优化模型。

如下图是生成的一些图片的效果：

PixelRNN 和 PixelCNN 能显式地计算似然 $p(x)$，是一种可优化的显式密度模型，该方法给出了一个很好的评估度量，可以通过计算的数据的似然来度量出生成样本有多好。但是序列化的生成方式使得无论是 Pixel CNN还是RNN速度都比较慢。

3. 变分自编码器VAE

本章节部分参考了 北京邮电大学 鲁鹏 的计算机视觉课程

3.1 自编码器

自编码器是为了无监督地学习出样本的特征表示，原理如下：

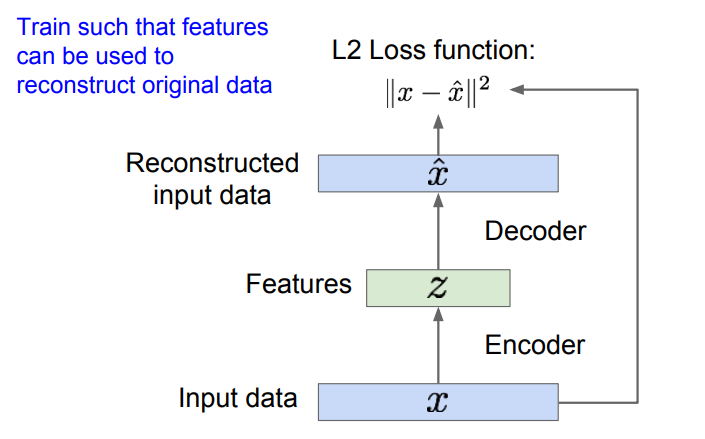
如上图，自编码器由编码器和解码器组成，编码器将样本 $x$ 映射到特征 $z$ ，解码器再使用特征 $z$ 重构样本。我们设定损失函数为输入的样本 $x$ 与重构样本之间的 L2 损失，以此训练出编码器和解码器的参数，希望能够使 $z$ 解码后恢复出原来的 $x$

编码器可以有多种形式，最先提出的是包含非线性层的线性组合，然后有了深层的全连接网络，后来又使用 CNN，我们通过神经网络对输入数据 $x$ 计算和映射，得到特征 $z$，$z$ 的维度通常比 $x$ 更小。所以这实际上就是一种降维，使用降维压缩可以保留 $x$ 中最重要的特征。

解码器主要是为了重构数据，它输出一些跟 $x$ 有相同维度的结果并尽量拟合 $x$。解码器一般使用和编码器相同类型的网络（与编码器对称)。

训练好完整的网络后，我们会把解码器的部分去掉，使用训练好的编码器实现特征的提取。通过编码器得到输入数据的特征，然后我们就可以使用这些特征训练一个分类器，实现监督学习中的分类任务。

所以，使用无标签数据训练得到的模型，可以帮助我们得到普适特征（比如上述自编码器映射得到的特征），它们作为监督学习的输入是非常有效的（有些场景下监督学习可能只有很少的带标签的训练数据，少量的数据很难训练模型，可能会出现过拟合等其他一些问题），通过上述方式得到的特征可以很好地初始化下游监督学习任务的网络。自编码器具有重构数据、学习数据特征、初始化一个监督模型的能力。这些学习到的特征具有能捕捉训练数据中蕴含的特征的能力，换句话说，通过编码器我们可以获得了一个含有训练数据中变化因子的隐变量 $z$ 。

3.2 VAE思想

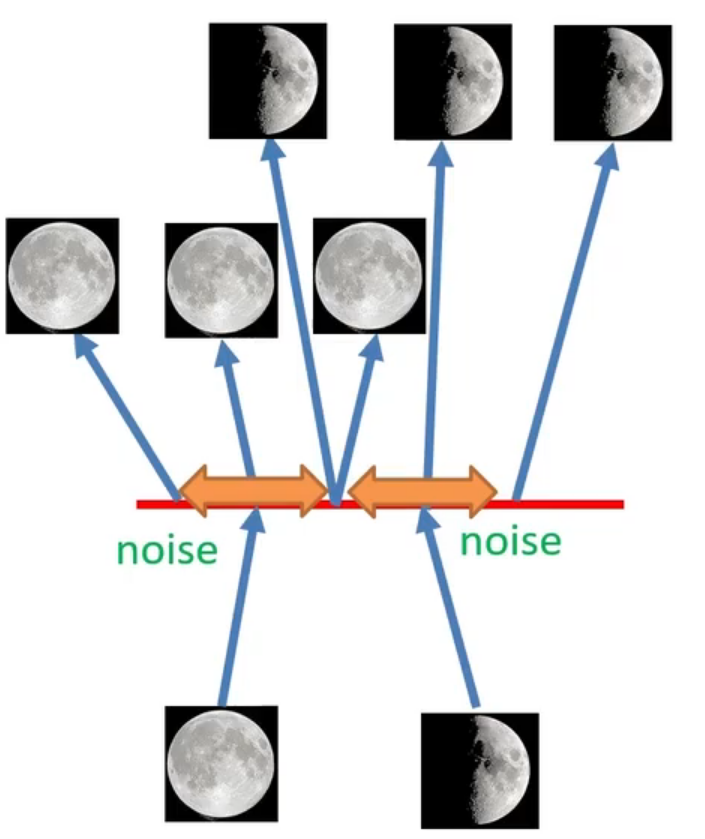
上一节提到我们使用编码器和解码器训练了一个可以提取输入中隐变量的编码器，其中编码器负责提取这个隐变量，解码器负责将隐变量映射回图片，协助模型训练。那么，既然解码器负责生成图片，那么我们能否利用这个解码器，使用随机的编码来生成一些新的图片呢？这不就是本文在讨论的生成模型的任务吗。但是，问题没有那么简单，因为我们训练的神经网络只是稀疏地记录了一对一的映射关系。举个例子，如下图所示。假设使用编码器我们将一张满月和一张半弦月映射成了两个编码（即隐变量$z$），然后也成功地将两个编码映射成了和输入一模一样的图片，这些都是能靠神经网络自学习实现的。但是，假设我们在这个码空间的中间采样一个编码，将其送入解码器，解码器可不会输出一个介于满月和半弦月之间的图片。原因就在于，神经网络只学会了对输入图片提取特征，并将这些特征恢复回图片，即只学会了对特定编码的解码。而对于码空间里的其他取值，神经网络连学都没学过，不可能正确地进行解码。所以就需要变分自编码器VAE。

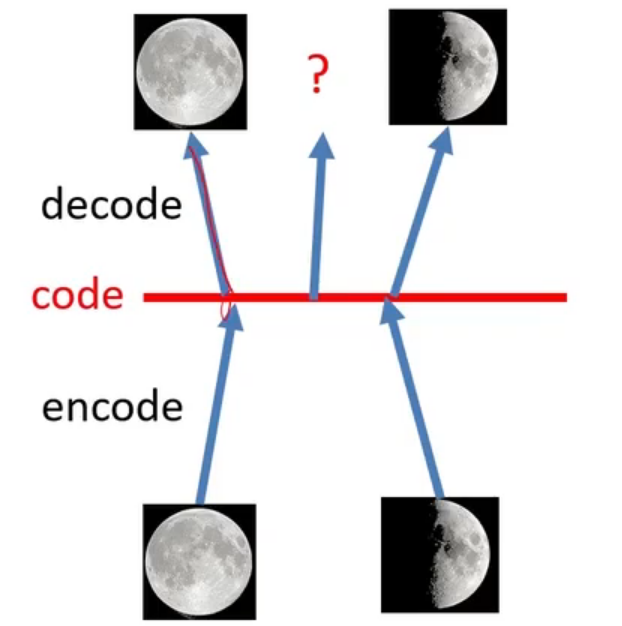
VAE不是直接输出隐变量 $z$ 而是输出图像的概率分布（假定为高斯分布），即同时输出均值和方差（使用多重任务损失，下面会介绍到），如下图其中 $m$ 表示分布的均值， $\sigma$ 表示分布的方差，所以真正的编码 $c$ 通过一个随机的噪声值 $e$ 在分布上进行采样得到的，即 $c = m + \exp(\sigma)e$ ，下图中有三个值分别表示RGB三个通道。 $\exp$ 表示对 $e$ 取指数，这样可以保证值非负。

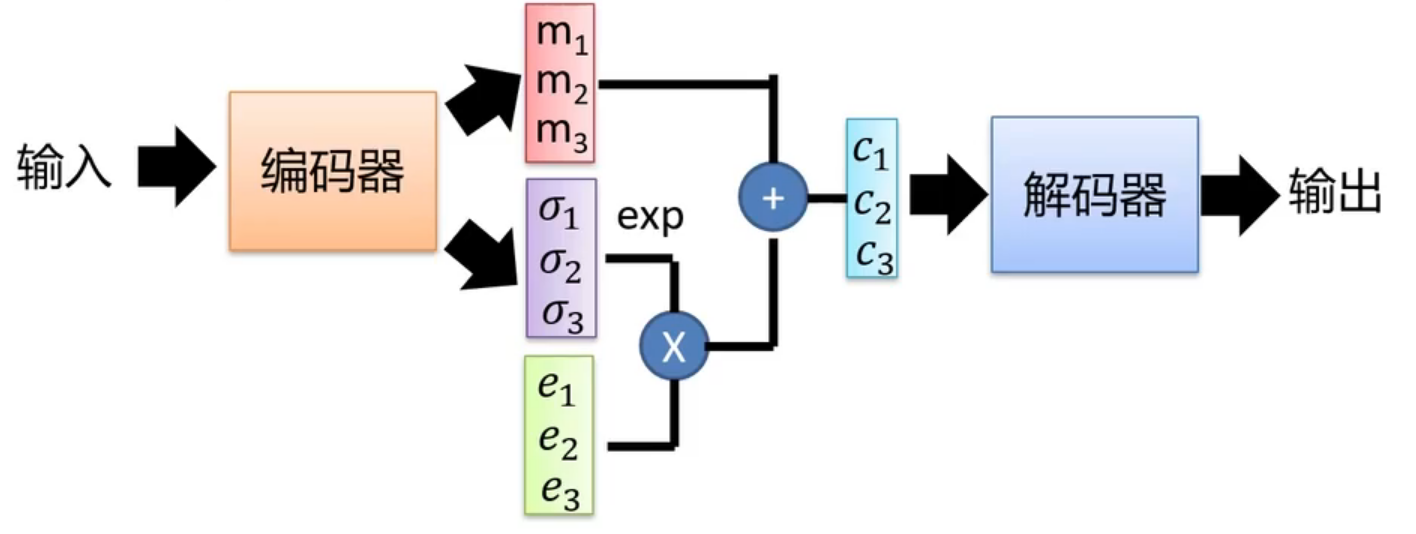
再来看训练过程，如果我们和自编码器一样只使用L2 损失项作为损失函数的话，那么上图所示的模型会退化成一个自编码器，因为模型完全可以将 $\sigma$ 都学成0，然后将 $m_1$ 当做隐变量，像自编码一样地去学习就行了。所以，我们需要重构一个损失函数，除了L2损失项保持不动外，还新增了一个损失项，其表达式如下：

其中 $\exp \left(\sigma_{i}\right)-\left(1+\sigma_{i}\right)$ 如下图绿线所示，如果求最小值，那么就是 $\sigma_i = 0$ 处，这使得 $\exp(\sigma) = 1$ ，也就是说让新的方差接近1（虽然 $\sigma$ 为方差，但是由于都是网络学习的，所以 $\exp(\sigma)$ 也可以看成新的方差） ，而式子中剩下的 $m_i^2$ 相当于一个正则项，使得编码器生成的编码分布比较均匀。

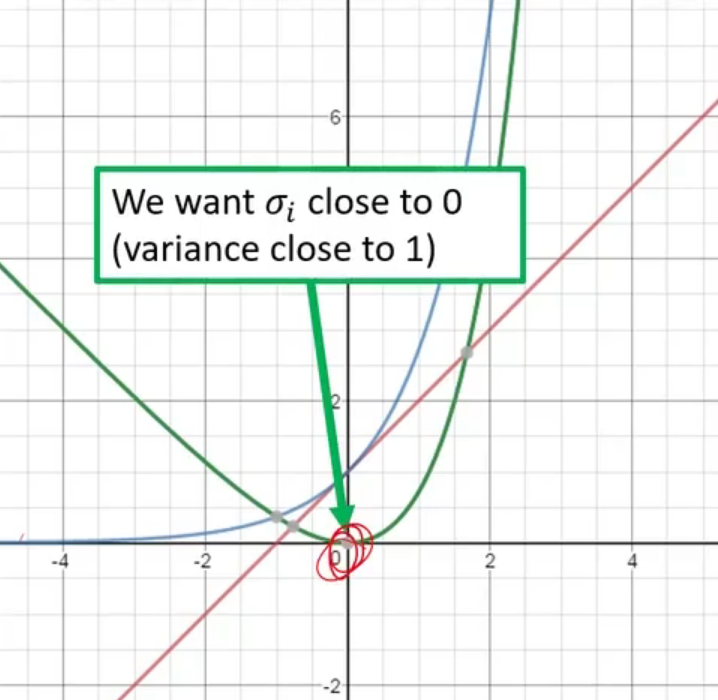
下面再来考虑，为什么VAE先生成概率分布，然后再使用一个噪声从概率分布中采样得到一个编码。如下图，对于一张满月的图，由于现在是一个正态分布，所以原来使用自编码器生成的编码位置的周围一些码空间也会以一定概率被采样用于学习如何生成满月图片，对于半弦月也同理。所以，在半弦月和满月之间的位置会被同时采样用于学习生成满月和半弦月，那么如果我们从这些位置采样，就会生成一张介于满月和半弦月之间的图片，这是因为它即要满足满月的特征，又要满足半弦月的特征。

3.3 VAE推导

本人学习时能力有限，学的比较乱，有些概念和定义理解不是很深刻，以后慢慢填坑吧

混合高斯模型

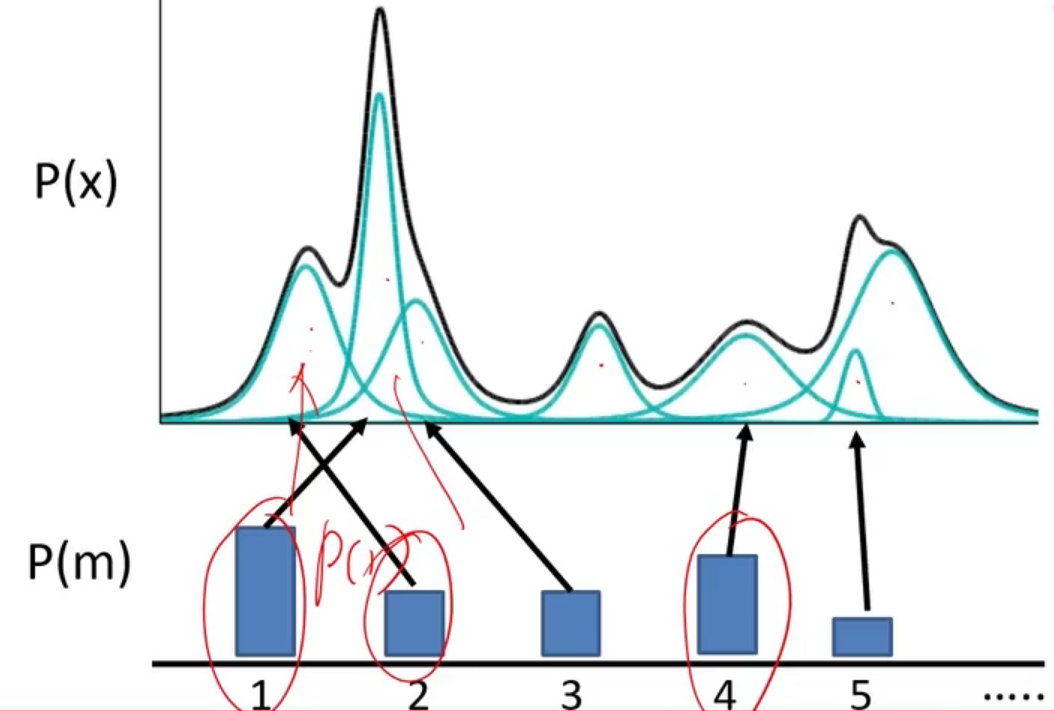
我们可以使用分布来描述一个事物，正态分布（即高斯分布）是一个很经典的分布，自然界很多东西都符合正态分布，但是使用单一的正态分布表达能力有限，于是我们就想到使用多个正态分布组合起来表示，如下图所示，黑色的曲线表示需要去拟合的真实分布，我们可以用若干个高斯分布来共同实现对真实分布的拟合。我们使用 $p(x) = \sum_m p(m)p(x|m)$ 来表示一个高斯混合模型，其中 $m$ 表示混合模型中一共有几个正态分布， $p(m)$ 表示取到下标为 $m$ 的正态分布的概率， $p(x|m)$ 表示在取到正态分布 $m$ 的条件下，横坐标取值为 $x$ 的概率。需要采样时，我们首先会从 $m$ 个正态分布中选一个，然后再对其用一个值 $x$ 进行采用。用表达式表示就是，首先 $m \sim p(m)$ ，即 $m$ 满足分布 $p(m)$ ，显然这是一个多项式分布。然后就是 $x|m\sim N(\mu^m,\sum^m)$ ，表示从一个正态分布 $N(\mu^m,\sum^m)$ 中采样 $x$ 。

 

VAE中使用混合高斯模型

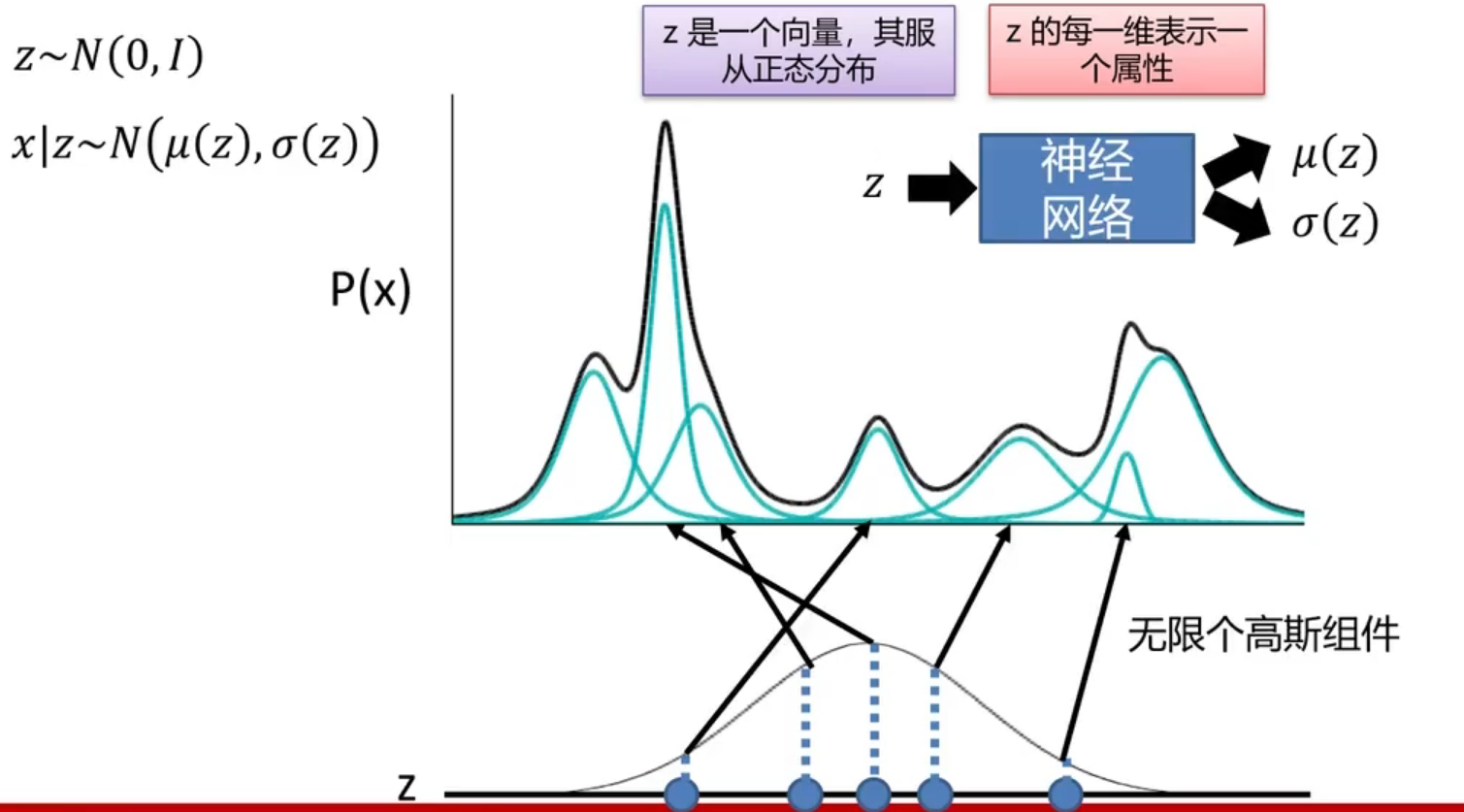
首先，我们编码器先获得一个服从正态分布的向量 $z$（输入） ，然后我们使用神经网络学习，使得随机从 $z$ 中采样一个值就能通过编码器（神经网络）获得一个高斯分布的参数 $\mu(z)$ 和 $\sigma(z)$ ，这其实就对应了混合高斯模型中的一个高斯分布组件，也就是说，由于 $z$ 是一个连续值，所以理论上这里的混合高斯模型中存在无限个高斯组件。由于 $z$ 的取值变成了连续的，所以混合高斯模型的表达式也变成了积分的形式：$P(x)=\int_{z} P(z) P(x \mid z) d z$。值得考虑的是，这里的 $z$ 的每一维度可以理解为图片的某个属性（比如如果是人脸，就可以类比成是否有胡子、是否戴眼镜等这些属性）。

个人理解，可能就是通过一个CNN提取出一个特征向量（比如1000维的特征向量），然后将特征向量作为输入送入编码器作为 $z$ 。

极大似然估计

现在，我们就需要寻找一个办法可以来训练这个神经网络使得其对于任意的 $z$ 都可以生成一个合适的分布，使得整个高斯混合模型可以很好地拟合输入图像的分布，自然而然的我们就想到了可以使用极大似然估计法，因为现实存在的一定就是概率最大的嘛。首先，当前的高斯混合模型公式为：

其中，$P(z)$ 满足正态分布，$x|z \sim N(\mu(z),\sigma(z))$，$\mu(z),\sigma(z)$ 是神经网络需要学习的内容。使用极大似然估计法可以得到似然函数：

也就是说，我们希望神经网络可以通过更新参数，使得生成的一系列分布，让他们的似然值尽量大，也就和输入数据的真实分布越接近。但是这个式子无法用于求最大值，因为其中的 $z$ 的分布是隐含的，而不是显式给出的，我们总不能穷举所有 $P(z)$ 吧，这是不现实的。并且 $P(x|z)$ 是通过神经网络计算得来的，也不能直接用数学方式求出。所以我们用一个近似的办法，由于在 $z$ 的取值空间中并不是所有的值都能生成一个高斯组件，大部分的 $z$ 是无法生成高斯组件的，所以我们使用另外一个分布 $q(z|x)$ ，表示在输入数据为 $x$ 的时候，可以产生哪些 $z$ 。即 $z \mid x \sim N\left(\mu^{\prime}(x), \sigma^{\prime}(x)\right)$，给定一个 $x$ 可以产生一个 $z$ 的分布。于是可以进行公式推导：

也就是说，我们如果想要 $\log P(x)$ 越大，那么只要让 $\int_{z} q(z \mid x) \log \left(\frac{P(x \mid z) P(z)}{q(z \mid x)}\right) d z$ 越大就好，这称为下界函数 $L_b$ ，这也是机器学习中的一种优化方法，即找到一个近似解作为下界，让下界最大，那么我们的目标也会最大。我们对 $L_b$ 进一步处理，得到：

其中，右边一项等于 $-K L(q(z \mid x) \| P(z))$ 即负的KL散度，可知取值为 负无穷到0，要使得 $L_b$ 越大，那么就要KL散度越接近0，也就是说，让 $q$ 的分布越接近 $P$ 的分布，而 $P$ 的分布为一个正态分布，所以就是让方差接近1，这就和前面介绍VAE损失函数新增的损失项 $\sum_{i=1}^{3}\left(\exp \left(\sigma_{i}\right)-\left(1+\sigma_{i}\right)+\left(m_{i}\right)^{2}\right)$ 的目标一致了。再来看 $\int_{z} q(z \mid x) \log P(x \mid z) d z$ 这一项，这表示给定一个 $x$ 生成了一个 $z$ ，然后又用 $z$ 重构了一个 $z$ ，而想让这项越大越好，也就是说让 $x$ 生成 $z$ ，再让 $z$ 重构 $z$ 的概率越大越好，即让两者越相似越好，这就和L2损失项对应了，具体过程如下图：

3.4 总结

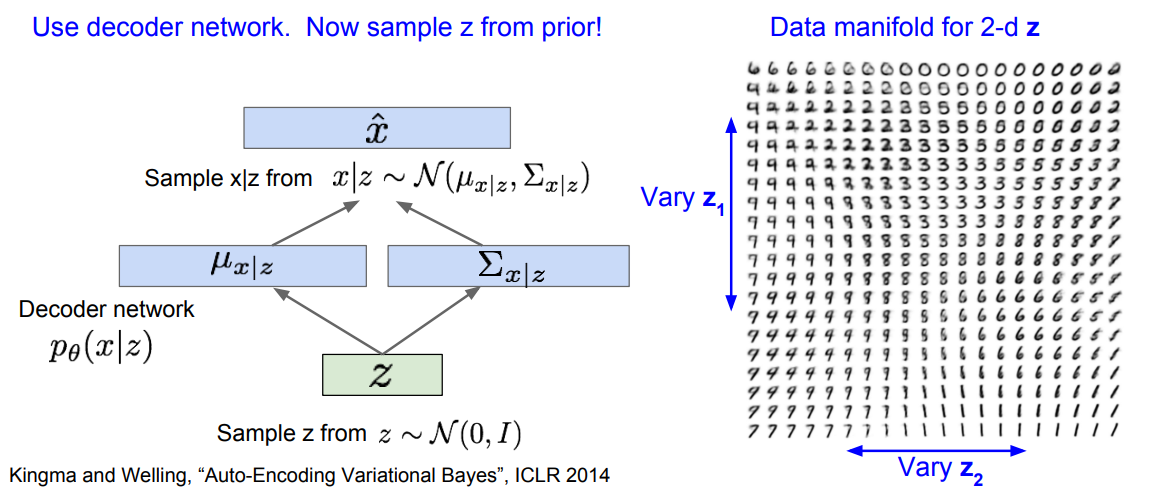
使用VAE训练后，将编码器去除，只保留解码器，于是就可以在码空间中任意取值，解码器就会自动生成图片，如下图所示。

4. 生成对抗网络GAN

GAN 的全称为 Generative Adversarial Nets，它解决了训练样本的分布维度高，难以采样的问题。其解决方法类似VAE，使用一个简单的分布进行采样， 然后使用神经网络学习一种映射可以将其转变到训练样本的分布。

4.1 两个玩家的游戏

在GAN中，有两个神经网络：

• 生成网络：期望能够产生尽量真实的图片，进而欺骗判别器
• 判别网络：期望能够准确地区分真假图片

如下图所示，可以将生成网络比作一个制造伪钞的骗子，而判别网络比作一个验钞机。骗子就期望可以制造尽量逼真的网络骗过验钞机，使得其可以在市场流通。而验钞机则希望，尽可能地能区分出伪钞和真钞。这样一个模型的训练流程是这样的，一开始只有真钱，骗子随机生成一个图片作为假钞送入验钞机，由于验钞机一开始没有辨别真伪的能力，所以认为这个伪钞是真的。当然，这个伪钞会被贴上一个标签来标识这是个伪钞，于是银行系统发现了这个伪钞没有被验钞机识别出来。于是，验钞机学习这个1.0版本的伪钞和真钞之间的区别，更新升级至2.0版本，成功区分出这个1.0版本的伪钞。接着，骗子继续使用同样的方式随机生成一张1.0版本的伪钞，发现无法欺骗验钞机了。于是，骗子也开始升级自己的技术，学习真钞中的特征使得生成的伪钞更接近真钞，于是骗子生成了2.0版本的伪钞，成功骗过了验钞机。验钞机继续学习2.0版本的伪钞和真钞的区别，升级至3.0版本……如此往复，直到骗子的伪造能力非常高超以至和真钞几乎没有区别为止。可以看到，模型的学习过程就是两个网络相互抗衡斗争的过程，这也是GAN中的Adversarial的来源。

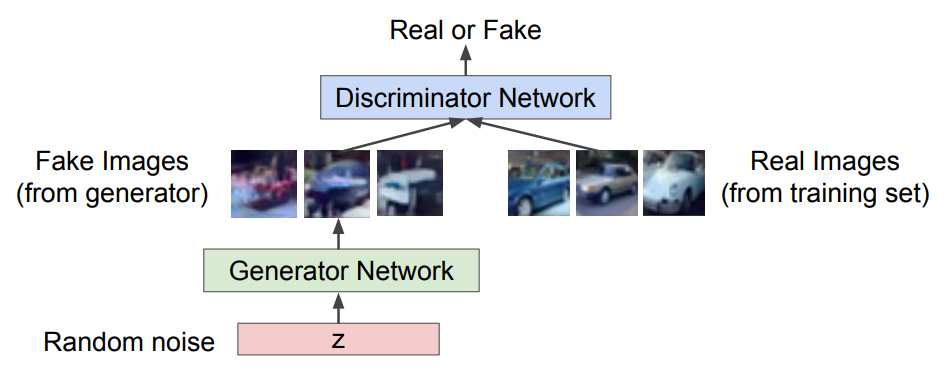
4.2 目标函数

将上述的对抗过程写成数学表达形式，如下所示。其中，$p_{data}$ 表示数据的分布，$p_{(z)}$ 表示噪声的分布，$G_{\theta_g}$ 表示带有参数 $\theta_g$ 的生成网络，使用 $G_{\theta_g}(z)$ 可以生成一个样本 $x$。同理，$D$ 表示一个判别网络，使用 $D_{\theta_d}(x)$ 可以对输入的 $x$ 进行判别真伪，输出一个 0-1 的概率（0表示假，1表示真），而表达式中的 $\mathbb{E}$ 表示我们考虑的是整个训练集中所有样本的一个期望，而不是具体某个样本的概率。

所以，上式的意思我们可以分两步来看：

首先，我们希望通过调整 $\theta_d$ 使得整个表达式越大越好，也就是说首先希望 $\mathbb{E}_{x \sim p_{d a t a}} \log D_{\theta_{d}}(x)$ 越大越好，即判别器对于真实样本的判别为真的期望越大越好。其次就是，希望 $\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$ 越大越好，也就是希望 $D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)$ 越小越好，也就是希望判别器对假的样本判别为真的概率越小越好（这里只考虑生成器，所以 $G_{\theta_{g}}(z)$ 可以看成一个固定值，表示一个伪造样本）。

其次，我们还希望通过调整 $\theta_g$ 使得整个式子越小越好，表达式中前半项和 $\theta_g$ 无关，主要是后半项。想要整个式子越小，也就是让 $D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)$ 越大越好，也就是说希望生成器判别伪造样本为真的概率越大越好。注意，这里我们是固定了 $\theta_d$ ，只考虑 $\theta_g$ ，也就是说我们希望更新生成器的参数 $\theta_g$ 使得其能生成能骗过判别器的假样本。

总的而言，其训练方式如下：

4.3 训练流程

既然有了目标函数，我们就可以训练模型了，训练过程中，我们将目标函数拆分开交替进行：

• 首先使用 梯度上升 进行 $\max _{\theta_{d}}\left[\mathbb{E}_{x \sim p_{\text {data }}} \log D_{\theta_{d}}(x)+\mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)\right]$，即训练判别器。一般来说，训练都是以判别器开始的。因为，一开始我们就可以随机生成图片，假设训练集中有1000张图片，那么我们就可以随机生成1000张图片，然后训练判别器使其能够区分这2000张图片即可。
• 然后进行 梯度下降 进行 $\min _{\theta_{g}} \mathbb{E}_{z \sim p(z)} \log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$ ，即训练生成器。
• 将上述两个过程交替进行即可。

然后实际训练时，对于生成器的训练不会使用 梯度下降 和最小化的目标函数，如下图的蓝色曲线为 $\log \left(1-D_{\theta_{d}}\left(G_{\theta_{g}}(z)\right)\right)$，可以看到，曲线一开始比较平缓，梯度很小，而在后面梯度很大。这就导致一个问题，由于初始随机生成的图片一般比较糟糕，所以 $D(G(z))$ 的值很接近 0，也就是说初始时的梯度很小，这就会导致模型训练很慢。而在生成的图片比较好的时候，梯度又很大，模型更新地会过快，这也不是我们想看到的，在即将收敛的时候应该放缓更新步伐。

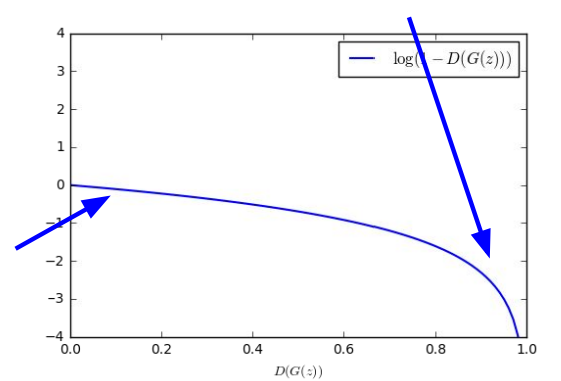
所以，我们会使用下式代替：

其图像如下图绿色曲线所示，它就有很好的特性，即初始时梯度大，最后梯度小，符合训练的需要，实际训练中基本都用这个式子。

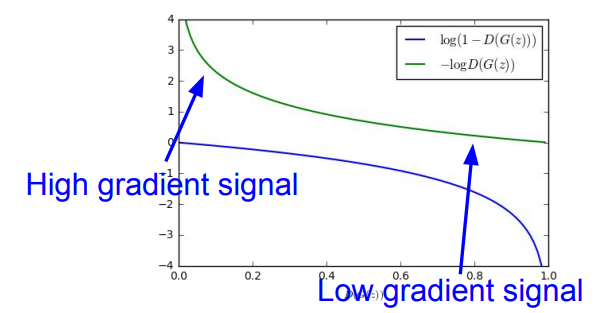
4.4 算法描述

4.5 总结